人教版数学八年级下册集训课堂练素养勾股定理解题的十种常见题型课件

这是一份人教版数学八年级下册集训课堂练素养勾股定理解题的十种常见题型课件，共25页。

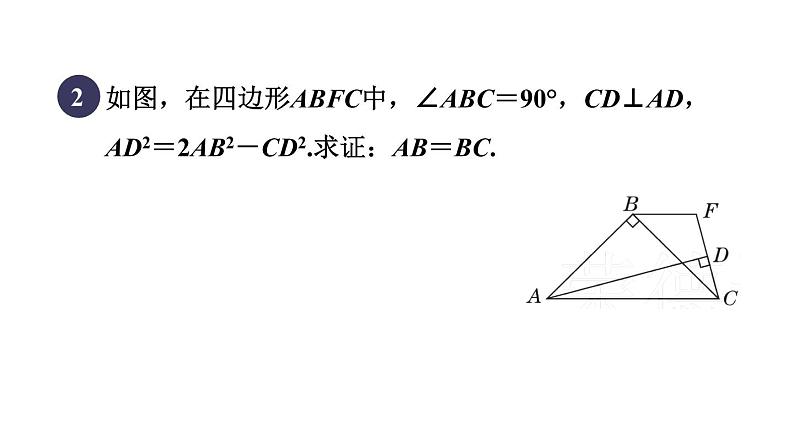
人教版 八年级下第十七章 勾股定理勾股定理解题的十种常见题型练素养　　课题 集训课堂7答 案 呈 现习题链接C172如图，在四边形ABFC中，∠ABC＝90°，CD⊥AD，AD2＝2AB2－CD2.求证：AB＝BC.证明：∵CD⊥AD，∴∠ADC＝90°，即△ADC是直角三角形．由勾股定理得AD2＋CD2＝AC2.又∵AD2＝2AB2－CD2，∴AD2＋CD2＝2AB2.∴AC2＝2AB2.∵∠ABC＝90°，∴△ABC是直角三角形．由勾股定理得AB2＋BC2＝AC2，∴AB2＋BC2＝2AB2.∴BC2＝AB2，∴AB＝BC.3如图，∠C＝90°，AM＝CM，MP⊥AB于点P.求证：BP2＝BC2＋AP2.证明：连接BM.∵PM⊥AB，∴△BMP和△AMP均为直角三角形．∴BP2＋PM2＝BM2，AP2＋PM2＝AM2.同理可得BC2＋CM2＝BM2，∴BP2＋PM2＝BC2＋CM2.∵CM＝AM，∴CM2＝AM2＝AP2＋PM2.∴BP2＋PM2＝BC2＋AP2＋PM2.∴BP2＝BC2＋AP2.4如图，在四边形ABCD中，AB＝AD＝8，∠A＝60°，∠D＝150°，四边形ABCD的周长为32，求BC和CD的长度．易得△BAE≌△BDE，∴BD＝AB＝8.又∵∠1＋∠2＝150°，∴∠2＝90°.设BC＝x，则CD＝16－x，由勾股定理得x2＝82＋(16－x)2，解得x＝10.∴BC＝10，CD＝6.5如图，将长方形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′处．若AB＝6，BC＝9，求BF的长．解：∵折叠前后两个图形的对应线段相等，∴CF＝C′F.设BF＝x，∵BC＝9，∴CF＝9－x.∴C′F＝9－x.由题意得BC′＝3.在Rt△C′BF中，根据勾股定理可得C′F2＝BF2＋C′B2，即(9－x)2＝x2＋32，解得x＝4.∴BF的长是4.6解：在Rt△ABC中，BC2＝AB2－AC2＝52－32＝16，∴BC＝4 cm.如图，在Rt△ABC中，∠ACB＝90°，AB＝5 cm，AC＝3 cm，动点P从点B出发沿射线BC以1 cm/s的速度移动，设运动的时间为t s.(1)求BC边的长；解：由题意知BP＝t cm，当△ABP为直角三角形时，有两种情况：Ⅰ.如图①，当∠APB为直角时，点P与点C重合，BP＝BC＝4 cm，则t＝4.(2)当△ABP为直角三角形时，借助图①求t的值；解：当△ABP为等腰三角形时，有三种情况：Ⅰ.如图①，当BP＝AB时，t＝5.Ⅱ.如图②，当AB＝AP时，BP＝2BC＝8 cm，t＝8.(3)当△ABP为等腰三角形时，借助图②求t的值．7如图，某学校(A点)到公路(直线l)的距离为300 m，到公交站(D点)的距离为500 m．现要在公路边上建一个商店(C点)，使之到学校A及公交站D的距离相等，求商店C与公交站D之间的距离．解：设CD＝x m，则AC＝x m.如图，作AB⊥l于点B，则AB＝300 m.在Rt△ABD中，AD2＝AB2＋BD2，AB＝300 m，AD＝500 m，∴BD＝400 m.∴BC＝(400－x)m.在Rt△ABC中，AC2＝AB2＋BC2，∴x2＝3002＋(400－x)2，解得x＝312.5.答：商店C与公交站D之间的距离为312.5 m.【传统文化】《九章算术》是古代东方数学代表作，书中记载：今有开门去阃(读kǔn，门槛的意思)一尺，不合二寸，问门广几何？题目大意是：如图①②(图②为图①的平面示意图)，推开双门，双门间隙C，D的距离为2寸，点C和点D距离门槛AB都为1尺(1尺＝10寸)，则AB的长是(　　)A．50.5寸　 B．52寸　 C．101寸　 D．104寸8【点拨】【答案】C9【教材P39复习题T12变式】如图，圆柱形玻璃容器高10 cm，底面周长为30 cm，在外侧距下底1 cm的点S处有一只蚂蚁，与蚂蚁相对的圆柱形容器的上口外侧距开口处1 cm的点F处有食物，求蚂蚁要吃到食物所走最短路线的长度．如图，桌子上放着一个长方体盒子，长、宽、高分别是12 cm，8 cm，30 cm，在AB的中点C处有一滴蜜糖，一只小虫从E处沿盒子表面爬到C处去吃．求小虫爬行的最短路程．情况二：如图②，连接EC.根据勾股定理可求得EC2＝82＋(30＋12＋15)2＝3 313.情况三：如图③，连接EC.根据勾股定理可求得EC2＝122＋(30＋8＋15)2＝2 953.∵625＜2 953＜3 313，∴小虫爬行的最短路程是25 cm.