人教版数学八年级下册集训课堂测素质特殊平行四边形的性质和判定课件

这是一份人教版数学八年级下册集训课堂测素质特殊平行四边形的性质和判定课件，共28页。

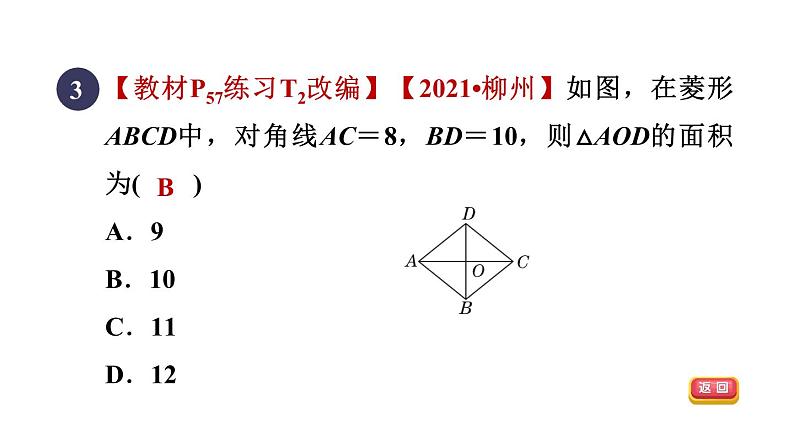
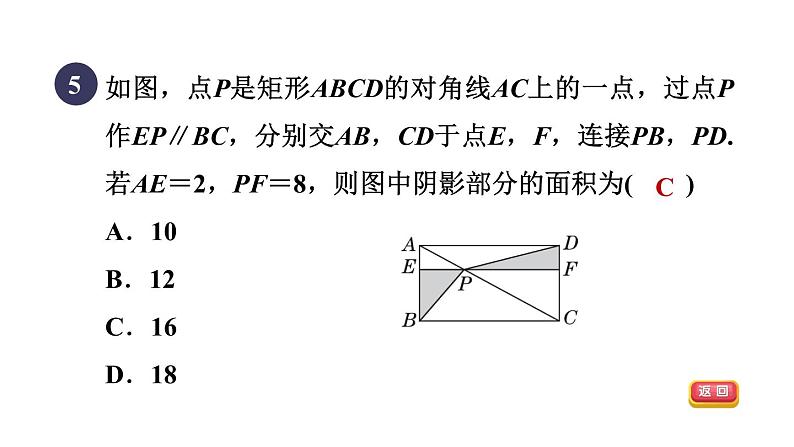
人教版 八年级下第十八章 平行四边形特殊平行四边形的性质和判定测素质　　课题 集训课堂CBCD答 案 呈 现习题链接CCB5216.8B习题链接在平行四边形、矩形、菱形、正方形中，既是轴对称图形又是中心对称图形的有(　　)A．1个 B．2个 C．3个 D．4个1C一、选择题(每题4分，共32分)D2【2022•陕西】在下列条件中，能够判定▱ABCD为矩形的是(　　)A．AB＝AC B．AC⊥BDC．AB＝AD D．AC＝BD【教材P57练习T2改编】【2021•柳州】如图，在菱形ABCD中，对角线AC＝8，BD＝10，则△AOD的面积为(　　)A．9 B．10 C．11 D．123B4B如图，点P是矩形ABCD的对角线AC上的一点，过点P作EP∥BC，分别交AB，CD于点E，F，连接PB，PD.若AE＝2，PF＝8，则图中阴影部分的面积为(　　)A．10 B．12 C．16 D．185C如图，顺次连接四边形ABCD各边中点得到四边形EFGH，要使四边形EFGH为矩形，应添加的条件是(　　)A．AB∥DC 　　B．AC＝BDC．AC⊥BD 　　D．AB＝DC6C7C8B9【2022•达州】如图，菱形ABCD的对角线AC，BD相交于点O，AC＝24，BD＝10，则菱形ABCD的周长为________．52二、填空题(每题5分，共20分)【2021•阜新】如图，折叠矩形纸片ABCD，使点B的对应点E落在CD边上，GH为折痕，已知AB＝6，BC＝10.当折痕GH最长时，线段BH的长为________．6.8【2022•无锡】如图，正方形ABCD的边长为8，点E是CD的中点，HG垂直平分AE且分别交AE，BC于点H，G，则BG＝______．1如图，在Rt△ABC中，∠BAC＝90°，且BA＝3，AC＝4，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为________．【点拨】(10分)【2022•山西】如图，在矩形ABCD中， AC是对角线．三、解答题(共48分)(1)实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD于点E，交边BC于点F；(要求：尺规作图并保留作图痕迹，不写作法，标明字母)解：如图．证明：AE＝CF，证明如下：∵四边形ABCD是矩形，∴AD∥BC，∴∠EAO＝∠FCO，∠AEO＝∠CFO.∵EF是AC的垂直平分线，∴AO＝CO.∴△AOE≌△COF(AAS)，∴AE＝CF.(2)猜想与证明：试猜想线段AE与CF的数量关系，并加以证明．(10分)【2021•菏泽】如图，在菱形ABCD中，点M，N分别在AB，CB上，且∠ADM＝∠CDN.求证：BM＝BN.(12分)【2022•遂宁】如图，在菱形ABCD中，对角线AC，BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF.(1)求证：△AOE≌△DFE；证明：∵点E是AD的中点，∴AE＝DE.∵DF∥AC，∴∠OAE＝∠FDE.∵∠AEO＝∠DEF，∴△AOE≌△DFE(ASA)．(2)判断四边形AODF的形状，并说明理由．解：四边形AODF为矩形，理由：∵△AOE≌△DFE，∴AO＝DF.∵DF∥AC，∴四边形AODF为平行四边形．∵四边形ABCD为菱形，∴AC⊥BD，即∠AOD＝90°.∴平行四边形AODF为矩形．(16分)【2021•荆门】如图，点E是正方形ABCD的边BC上的动点，∠AEF＝90°，且EF＝AE，FH⊥BH.(1)求证：BE＝CH；证明：∵四边形ABCD是正方形，∴∠B＝90°，AB＝BC.∵FH⊥BH，∴∠H＝90°＝∠B，∠EFH＝90°－∠FEH.　(2)连接DF，若AB＝3，BE＝x，用含x的代数式表示DF 的长．解：过点F作FP⊥CD于点P，如图所示．∵∠H＝∠DCH＝∠FPC＝90°，　∴四边形PCHF是矩形．由(1)知BE＝FH＝CH，∴四边形PCHF是正方形．