




初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理背景图ppt课件
展开
这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理背景图ppt课件,共18页。PPT课件主要包含了答案呈现,习题链接等内容,欢迎下载使用。
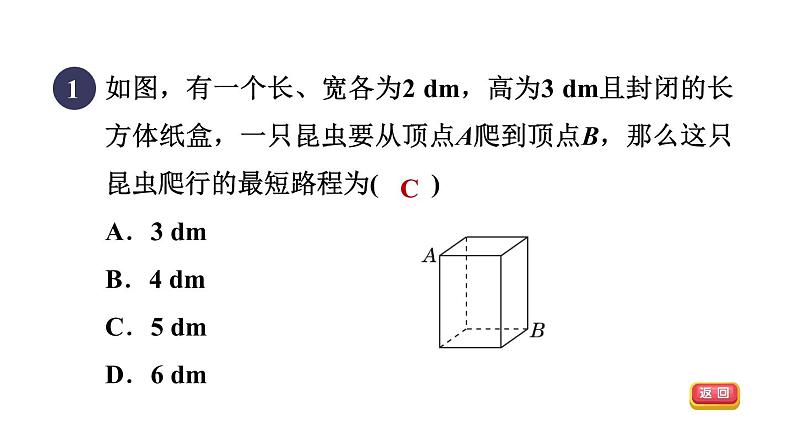
如图,有一个长、宽各为2 dm,高为3 dm且封闭的长方体纸盒,一只昆虫要从顶点A爬到顶点B,那么这只昆虫爬行的最短路程为( )A.3 dm B.4 dm C.5 dm D.6 dm
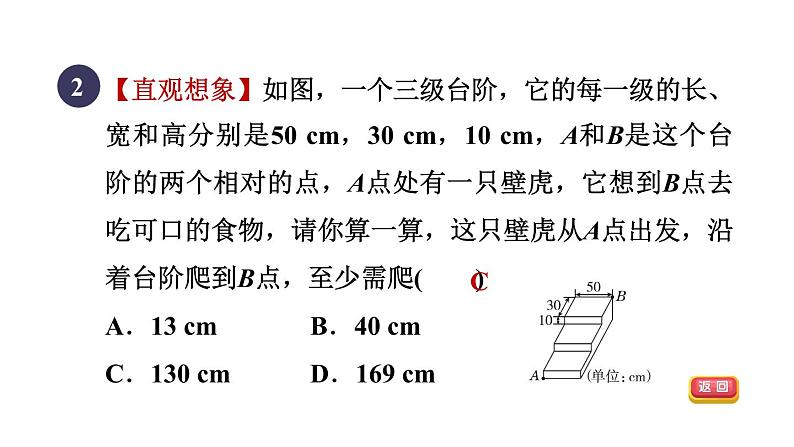
【直观想象】如图,一个三级台阶,它的每一级的长、宽和高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的点,A点处有一只壁虎,它想到B点去吃可口的食物,请你算一算,这只壁虎从A点出发,沿着台阶爬到B点,至少需爬( )A.13 cm B.40 cm C.130 cm D.169 cm
【教材P39复习题T12变式】如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从杯外壁点A处到杯内壁点B处的最短距离为________cm(杯壁厚度不计).
【点拨】本题考查最短路径问题.沿圆柱过点A的高将圆柱的侧面展开,得到长方形EFGH,过点B作BQ⊥EF于点Q,作点A关于EH的对称点A′,连接A′B交EH于点P,连接AP,如图所示,则AP+PB就是蚂蚁爬行的最短距离.
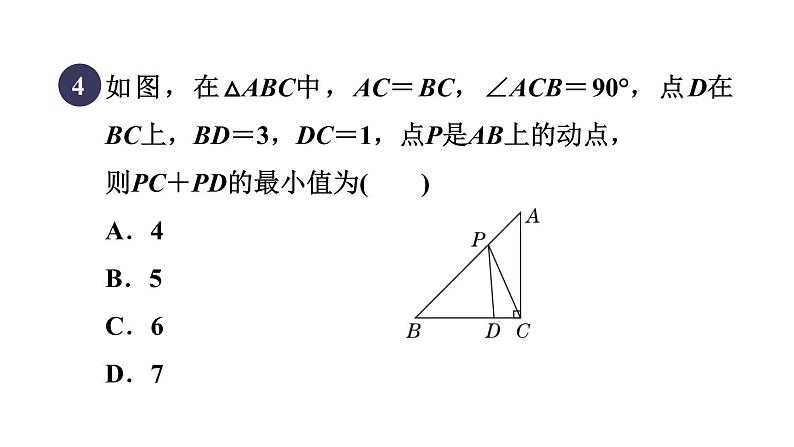
如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )A.4 B.5 C.6 D.7
【点拨】如图,过点C作CO⊥AB于点O,延长CO到点C′,使OC′=OC,连接DC′,交AB于点P′,连接CP′,此时DP′+CP′=DP′+P′C′=DC′的值即为PC+PD的最小值.
连接BC′,由对称性可知∠C′BP′=∠CBP′=45°,∴∠CBC′=90°.∵AB⊥CC′,OC=OC′,∴BC′=BC=3+1=4.根据勾股定理可得DC′=5.
【中考•恩施州】如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为( )A.5 B.6 C.7 D.8
【点拨】如图,连接ED交AC于点F′,连接BF′.∵四边形ABCD是正方形,∴点B与点D关于AC对称.∴BF′=DF′.∴△BF′E的周长=BF′+EF′+BE=DE+BE,此时△BEF的周长最小.由勾股定理得DE=5,则△BF′E的周长=DE+BE=5+1=6.
【2023•衡水至臻中学模拟】如图,已知长方体的长AC=2 cm,宽BC=1 cm,高AA′=4 cm.如果一只蚂蚁沿长方体的表面从A点爬到B′点,那么最短路程是多少?
如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400 m,BD=200 m,CD=800 m,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少?
解:如图,作点A关于直线CD的对称点A′,连接A′B交CD于点M,连接AM,则AM=A′M,所以在点M处饮水能使所走的总路程最短,最短路程为A′B的长.过点A′作A′H⊥BD,交BD的延长线于点H.
相关课件
这是一份人教版八年级下册17.1 勾股定理教课课件ppt,文件包含第2课时勾股定理的应用pptx、勾股定理的应用mp4等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
这是一份人教版八年级下册17.1 勾股定理精品课件ppt,共17页。PPT课件主要包含了复习回顾,问题1,几何语言,新知探究,探究一,问题2,木板可以斜着过吗,探究二,∴OB1,≈57m等内容,欢迎下载使用。
这是一份人教版八年级下册第十七章 勾股定理17.1 勾股定理精品ppt课件,共24页。PPT课件主要包含了∴OB1,数学问题,直角三角形,勾股定理,实际问题,蚂蚁A→B的路线,侧面展开图,数学思想,立体图形,平面图形等内容,欢迎下载使用。










