初中数学人教版九年级下册27.2.3 相似三角形应用举例授课ppt课件

这是一份初中数学人教版九年级下册27.2.3 相似三角形应用举例授课ppt课件，共16页。PPT课件主要包含了习题链接，2EF⊥AB等内容，欢迎下载使用。
如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB＝6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C.(1)求证：AD平分∠BAC；
证明：如图，连接OD.∵BD是⊙O的切线，∴OD⊥BD.∵AC⊥BD，∴OD∥AC.∴∠DAC＝∠ADO.∵OA＝OD，∴∠DAO＝∠ADO.∴∠DAO＝∠DAC，即AD平分∠BAC.
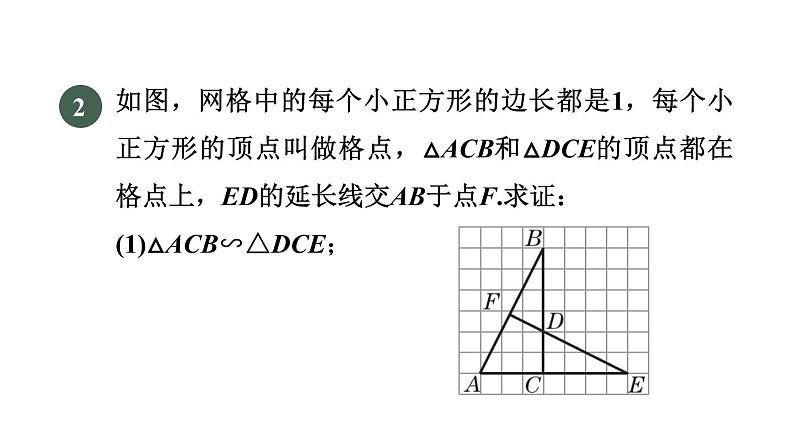
如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点，△ACB和△DCE的顶点都在格点上，ED的延长线交AB于点F.求证：(1)△ACB∽△DCE；
解：∵△ACB∽△DCE，∴∠ABC＝∠DEC.又∵∠ABC＋∠BAC＝90°，∴∠DEC＋∠BAC＝90°.∴∠EFA＝90°.∴EF⊥AB.
【教材P58复习题T8拓展】如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC2＝PE·PO.(1)求证：PC是⊙O的切线；
(2)若OE：EA＝1：2，PA＝6，求⊙O的半径．
【2021·铜仁】如图，已知△ABC内接于⊙O，AB是⊙O的直径，∠CAB的平分线交BC于点D，交⊙O于点E，连接EB，作∠BEF＝∠CAE，交AB的延长线于点F.(1)求证：EF是⊙O的切线；
证明：如图，连接OE，∵AB是⊙O的直径，∴∠AEB＝90°，即∠AEO＋∠OEB＝90°.∵AE平分∠CAB，∴∠CAE＝∠BAE.∵∠BEF＝∠CAE，∴∠BEF＝∠BAE.∵OA＝OE，∴∠BAE＝∠AEO，∴∠BEF＝∠AEO，∴∠BEF＋∠OEB＝90°，∴∠OEF＝90°，∴OE⊥EF.∵OE是⊙O的半径，∴EF是⊙O的切线．
(2)若BF＝10，EF＝20，求⊙O的半径和AD的长．
解：设⊙O的半径为x，则OE＝OB＝x，∴OF＝x＋10，在Rt△OEF中，由勾股定理得OE2＋EF2＝OF2，即x2＋202＝(x＋10)2，解得x＝15，∴⊙O的半径为15.∵∠BEF＝∠BAE，∠F＝∠F，∴△EBF∽△AEF，