2022-2023学年江苏省淮安市淮安区八年级（上）期中数学试卷（含解析）

这是一份2022-2023学年江苏省淮安市淮安区八年级（上）期中数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

第I卷（选择题）
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
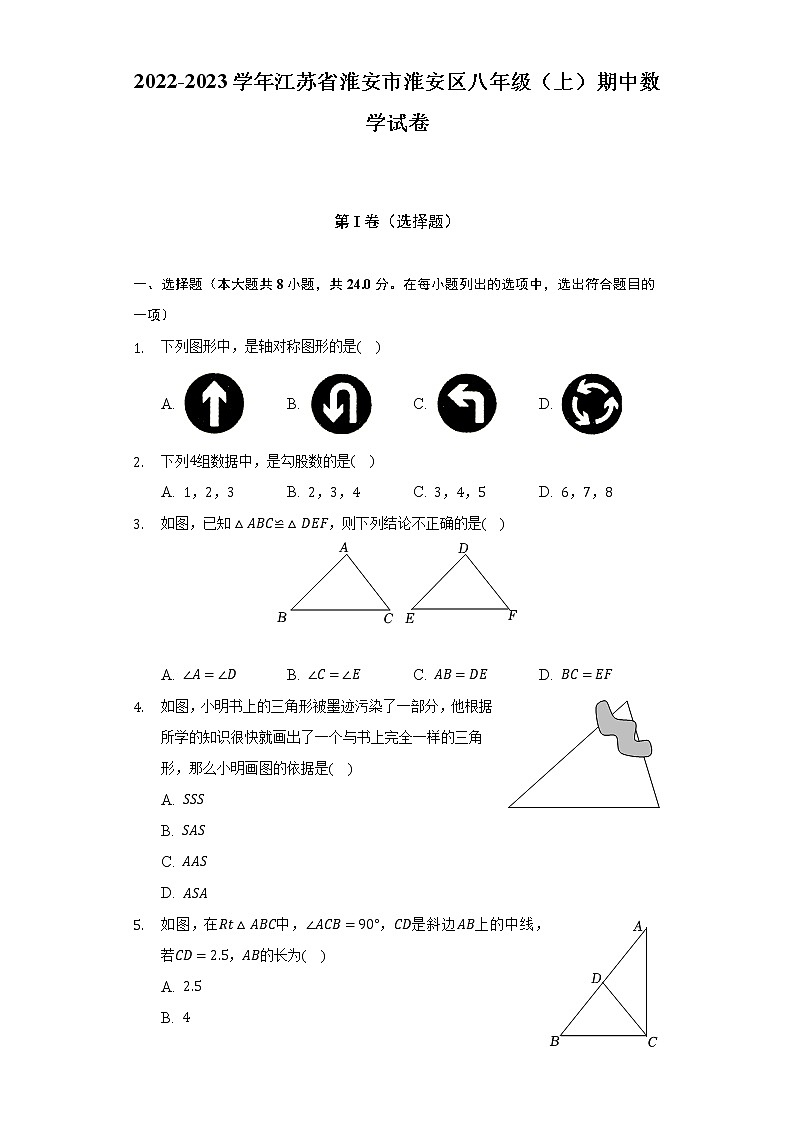
下列图形中，是轴对称图形的是( )
A. B. C. D.
下列4组数据中，是勾股数的是( )
A. 1，2，3B. 2，3，4C. 3，4，5D. 6，7，8
如图，已知△ABC≌△DEF，则下列结论不正确的是( )
A. ∠A=∠DB. ∠C=∠EC. AB=DED. BC=EF
如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画出了一个与书上完全一样的三角形，那么小明画图的依据是( )
A. SSS
B. SAS
C. AAS
D. ASA
如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，若CD=2.5，AB的长为( )
A. 2.5
B. 4
C. 5
D. 6
如图，在四个均由十六个小正方形组成的正方形网格中，各有一个三角形，那么这四个三角形中，不是直角三角形的是( )
A. B.
C. D.
如图，Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A'处，折痕为CD，则∠A'DB=( )
A. 40°
B. 30°
C. 20°
D. 10°
如图，BO平分∠ABC，CO平分∠ACB，MN//BC，AB=15，AC=18，则△AMN的周长为( )
A. 15
B. 18
C. 30
D. 33
第II卷（非选择题）
二、填空题（本大题共8小题，共24.0分）
已知△ACB≌△A'CB'，∠B=70°，则∠B'的度数为______．
如图，∠ABC=∠DCB，要用SAS判断△ABC≌△DCB，需要增加一个条件：______．
如图，P是∠AOB的平分线OC上一点，PD⊥OB，PE⊥OA，垂足分别为D，E，若PD=3，则PE的长是______．
如图所示：已知两个正方形的面积，则字母A所代表的正方形的面积为______．
在△ABC中，若三条边的长度分别为3、4、5，则这个三角形的面积是______．
如图，在△ABC中，AC=4，线段AB的垂直平分线交AB于点M，交AC于点N，若△BCN的周长为7，则BC=______．
等腰三角形ABC中，AB=5，BC=2，则AC的长为______．
在△ABC中，AB=AC=5，BC=6.若点P在边AC上移动，则BP的最小值是______．
三、解答题（本大题共11小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
(本小题6.0分)
如图，△ACF≌△ADE，AC=11，AF=5，求DF的长．
(本小题6.0分)
如图，AB=CD，∠B=∠C，点F、E在BC上，BF=CE.求证：∠AEB=∠DFC．
(本小题6.0分)
在△ABC中，∠C=90°，BC：AB=3：5且AB=20cm，求边AC的长度．
(本小题6.0分)
如图，甲乙两船从港口A同时出发，甲船以16海里/时的速度向北偏东40°航行，乙船向南偏东50°航行，12小时后，甲船到达C岛，乙船到达B岛，若CB两岛相距17海里，问乙船的航速是多少？
(本小题6.0分)
如图：已知OA和OB两条公路，以及C、D两个村庄，建立一个车站P，使车站到两个村庄距离相等即PC=PD，且P到OA，OB两条公路的距离相等．
(本小题6.0分)
如图，在四边形ABCD中，DE垂直平分AB，DF垂直平分BC，垂足分别为E，F．
(1)试说明DA=DC；
(2)如果∠A=70°，∠C=60°，求∠ADC的度数．
(本小题6.0分)
如图，在8×8的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC(即三角形的顶点都在格点上)．
(1)在图中作出△ABC关于直线l对称的△A1B1C1.(要求：A与A1，B与B1，C与C1相对应)
(2)在直线l上找一点Q，使QB+QC的值最小．
(本小题6.0分)
已知，如图，△ABC中，AB=AC，动点D、E、F在AB、BC、AC上移动，移动过程中始终保持BD=CE，∠DEF=∠B，请你分析是否存在始终与△BDE全等的三角形，并说明理由．
(本小题6.0分)
如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，过点D作DE⊥AB于点E，若CD=3，BD=5，求AE的长．
(本小题8.0分)
森林火灾是一种常见的自然灾害，危害很大，随着中国科技、经济的不断发展，开始应用飞机洒水的方式扑灭火源．如图，有一台救火飞机沿东西方向AB，由点A飞向点B，已知点C为其中一个着火点，且点C与直线AB上两点A，B的距离分别为600m和800m，又AB=1000m，飞机中心周围500m以内可以受到洒水影响．
(1)着火点C受洒水影响吗？为什么？
(2)若飞机的速度为10m/s，要想扑灭着火点C估计需要13秒，请你通过计算判断着火点C能否被扑灭？
(本小题10.0分)
如图，在△ABC中，∠B=90°，AB=16cm，BC=12cm，AC=20cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
(1)BP=______(用t的代数式表示)
(2)当点Q在边BC上运动时，出发几秒后，△PQB是等腰三角形？
(3)当点Q在边CA上运动时，出发______秒后，△BCQ是以BC或BQ为底边的等腰三角形？
答案和解析
1.【答案】A
【解析】解：选项A能找到这样一条直线，使这个图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
选项B、C、D不能找到这样一条直线，使这个图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
故选：A．
如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，据此判断即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】C
【解析】解：A.12+22≠32，因此不是勾股数，故此选项不合题意；
B.22+32≠42，因此不是勾股数，故此选项不合题意；
C.32+42=52，因此是勾股数，故此选项符合题意；
D.62+72≠82，因此不是勾股数，故此选项不合题意；
故选：C．
利用勾股数定义进行分析即可．
此题主要考查了勾股数，关键是掌握满足a2+b2=c2的三个正整数，称为勾股数．
3.【答案】B
【解析】解：∵△ABC≌△DEF，
∴∠A=∠D，∠C=∠F，AB=DE，BC=EF，
故选：B．
根据全等三角形的性质即可得到结论．
本题考查了全等三角形的判定和性质，熟练掌握全等三角形的性质是解题的关键．
4.【答案】D
【解析】解：根据题意，三角形的两角和它们的夹边是完整的，所以可以利用“角边角”定理作出完全一样的三角形．
故选：D．
根据图象，三角形有两角和它们的夹边是完整的，所以可以根据“角边角”画出即可．
本题考查了三角形全等的判定的实际运用，熟练掌握判定定理并灵活运用是解题的关键．
5.【答案】C
【解析】解：在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，
∴CD=12AB．
∴AB=2CD=2×2.5=5．
故选：C．
根据直角三角形的性质(直角三角形中斜边上的中线等于斜边的一半)解决此题．
本题主要考查直角三角形的性质，熟练掌握直角三角形中斜边上的中线等于斜边的一半是解决本题的关键．
6.【答案】A
【解析】解：选项A如图：

A、∵AC2=12+32=10，BC2=12+22=5，AB2=12+42=17，∴△ABC不是直角三角形，故本选项正确；
选项B如图：

B、∵AC2=22+42=20，BC2=12+22=5，AB2=32+42=25，∴△ABC是直角三角形，故本选项错误；
选项C如图：

C、∵AB2=22+22=8，AC2=22+22=8，BC2=16，∴△ABC是直角三角形，故本选项错误；
选项D如图：

D、∵AC2=12+32=10，BC2=12+32=10，AB2=22+42=20，∴△ABC是直角三角形，故本选项错误．
故选：A．
根据勾股定理的逆定理对各选项进行逐一判断即可．
本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
7.【答案】C
【解析】
【分析】
此题考查了直角三角形的性质，三角形的内角和定理，邻补角的定义，以及折叠的性质，熟练掌握性质是解本题的关键．在直角三角形ABC中，由∠ACB与∠A的度数，利用三角形的内角和定理求出∠B的度数，再由折叠的性质得到∠CA'D=∠A，再由∠CA'D+∠BA'D=180°，∠B+∠A'DB+∠BA'D=180°，得出∠CA'D=∠B+∠A'DB，即可求出∠A'DB的度数．
【解答】
解：在Rt△ABC中，∠ACB=90°，∠A=55°，
所以∠B=180°-90°-55°=35°，
由折叠可得：∠CA'D=∠A=55°，
又因为∠CA'D+∠BA'D=180°，∠B+∠A'DB+∠BA'D=180°，
所以∠CA'D=∠B+∠A'DB，
则∠A'DB=55°-35°=20°．
故选C．
8.【答案】D
【解析】解：∵BO平分∠ABC，CO平分∠ACB，
∴∠ABO=∠OBC，∠ACO=∠OCB，
∵MN//BC，
∴∠MOB=∠OBC，∠NOC=∠OCB，
∴∠ABO=∠MOB，∠ACO=∠NOC，
∴MB=MO，NO=NC，
∵AB=15，AC=18，
∴△AMN的周长=AM+MN+AN
=AM+MO+NO+AN
=AM+MB+NC+AN
=AB+AC
=33，
故选：D．
根据角平分线的定义和平行线的性质可得△MBO和△NCO是等腰三角形，从而可得MB=MO，NO=NC，然后利用等量代换可得△AMN的周长=AB+AC，进行计算即可解答．
本题考查了等腰三角形的判定与性质，平行线的性质，熟练掌握根据角平分线的定义和平行线的性质可证等腰三角形是解题的关键．
9.【答案】70°
【解析】解：∵△ACB≌△A'CB'，∠B=70°，
∴∠B'=∠B=70°．
故答案为：70°．
直接利用全等三角形的对应角相等进而得出答案．
此题主要考查了全等三角形的性质，正确得出对应角是解题关键．
10.【答案】AB=DC
【解析】
【分析】
本题考查了全等三角形判定的应用，能灵活运用全等三角形的判定定理进行推理是解此题的关键．条件是AB=DC，根据SAS推出即可．
【解答】
解：添加的条件是：AB=DC，
理由是：∵在△ABC和△DCB中
AB=DC∠ABC=∠DCBBC=CB
∴△ABC≌△DCB(SAS)，
故答案为：AB=DC．

11.【答案】3
【解析】解：∵P是∠AOB的平分线OC上一点，PD⊥OB，PE⊥OA，
∴PE=PD，
∵PD=3，
∴PE=3．
故答案为：3．
根据角平分线的性质定理可得答案．
本题考查角平分线的性质定理，熟练掌握角平分线的性质是解题关键．
12.【答案】64
【解析】解：由图形可知，字母A所代表的正方形的面积=289-225=64，
故答案为：64．
根据勾股定理结合正方形的面积公式即可求解．
本题考查了勾股定理，正方形的面积，熟练掌握勾股定理是解题的关键．
13.【答案】6
【解析】解：∵32+42=52，
∴△ABC是直角三角形，
∴S△ABC=12×3×4=6，
故答案为6．
首先证明△ABC是直角三角形，构建直角三角形的面积=直角边乘积的一半计算即可；
本题考查勾股定理的逆定理，直角三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
14.【答案】3
【解析】解：∵MN是线段AB的垂直平分线，
∴NA=NB，
∵△BCN的周长为7，
∴BC+CN+BN=7，
∴BC+CN+AN=BC+AC=7，
∴BC=7-AC=3，
故答案为：3．
根据线段垂直平分线的性质得到NA=NB，根据三角形的周长公式计算，得到答案．
本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
15.【答案】5
【解析】解：根据题意得5-2