河南省新乡市长垣县2022-2023学年九年级上学期期中数学试卷(含答案)

这是一份河南省新乡市长垣县2022-2023学年九年级上学期期中数学试卷(含答案)，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年河南省新乡市长垣县九年级第一学期期中数学试卷
一、选择题（每小题3分，共30分）
1．下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
2．一元二次方程2x2﹣5x+6＝0的根的情况为（　　）
A．无实数根 B．有两个不等的实数根
C．有两个相等的实数根 D．不能判定
3．点P（2，﹣1）关于原点对称的点P′的坐标是（　　）
A．（﹣2，1） B．（﹣2，﹣1） C．（﹣1，2） D．（1，﹣2）
4．如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB＝4，AC＝3，BC＝2，则BE的长为（　　）

A．5 B．4 C．3 D．2
5．若二次函数y＝2x2﹣3的图象上有两个点A（1，a），B（2，b），则a与b的大小关系（　　）
A．a＞b B．a＝b C．a＜b D．无法确定
6．一条排水管的截面如图所示，已知排水管的半径OB＝10，水面宽AB＝16，则截面圆心O到水面的距离OC是（　　）

A．4 B．5 C．6 D．6
7．随着生产技术的进步，某制药厂生产成本逐年下降．两年前生产一吨药的成本是5000元，现在生产一吨药的成本是4050元．设生产成本的年平均下降率为x，下面所列方程正确的是（　　）
A．5000（1+x）2＝4050 B．4050（1+x）2＝5000
C．5000（1﹣x）2＝4050 D．4050（1﹣x）2＝5000
8．如果将抛物线y＝2x2先向左平移2个单位，再向上平移3个单位后得到一条新的抛物线，这条新的抛物线的表达式是（　　）
A．y＝2（x﹣2）2+3 B．y＝2（x+2）2﹣3
C．y＝2（x﹣2）2﹣3 D．y＝2（x+2）2+3
9．如果一元二次方程ax2+bx+c＝0有两个根为x1，x2，那么方程的两个根x1，x2和系数a，b，c有如下关系：x1+x2＝﹣，x1x2＝．若m，n是方程x2+2x﹣2024＝0的两根，则2m﹣mn+2n＝（　　）
A．2020 B．﹣2028 C．﹣2020 D．2024
10．如图，一段抛物线y＝﹣x2+6x（0≤x≤6），记为抛物线C1，它与x轴交于点O、A1；将抛物线C1绕点A1旋转180°得抛物线C2，交x轴于点A2；将抛物线C2绕点A2，旋转180°得抛物线C3，交x轴于点A3；……如此进行下去，得到一条“波浪线”，若点M（17，m）在此“波浪线”上，则m的值为（　　）

A．﹣6 B．5 C．﹣4 D．0
二、填空题（每小题3分，共15分）
11．已知x＝1是方程x2+ax+3＝0的一个根，则a的值为　 　．
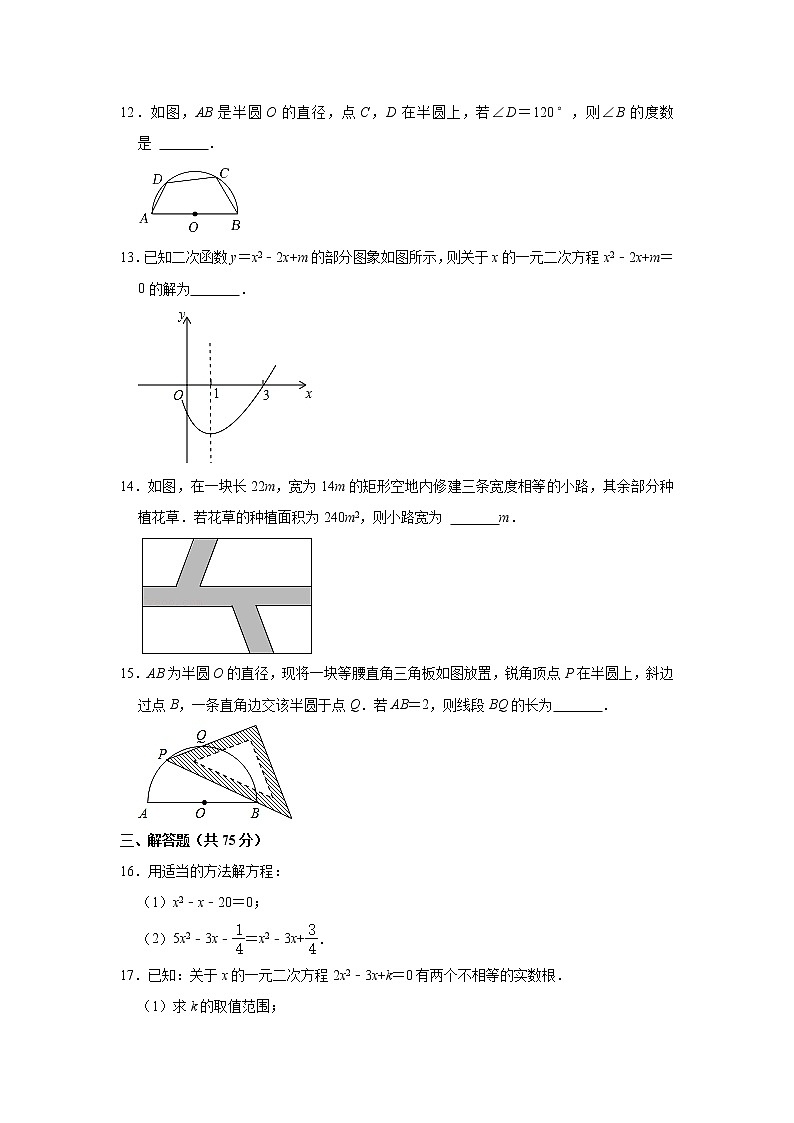
12．如图，AB是半圆O的直径，点C，D在半圆上，若∠D＝120°，则∠B的度数是 　 　．

13．已知二次函数y＝x2﹣2x+m的部分图象如图所示，则关于x的一元二次方程x2﹣2x+m＝0的解为　 　．

14．如图，在一块长22m，宽为14m的矩形空地内修建三条宽度相等的小路，其余部分种植花草．若花草的种植面积为240m2，则小路宽为 　 　m．

15．AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q．若AB＝2，则线段BQ的长为　 　．

三、解答题（共75分）
16．用适当的方法解方程：
（1）x2﹣x﹣20＝0；
（2）5x2﹣3x﹣＝x2﹣3x+．
17．已知：关于x的一元二次方程2x2﹣3x+k＝0有两个不相等的实数根．
（1）求k的取值范围；
（2）当k取最大整数值时，求该方程的解．
18．如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上．
（1）将△ABC向左平移6个单位长度得到△A1B1C1，请画出△A1B1C1；
（2）画出△A1B1C1关于点O的中心对称图形△A2B2C2；
（3）若将△ABC绕某一点旋转可得到△A2B2C2那么旋转中心的坐标为 　 　，旋转角度为 　 　°．

19．已知抛物线y＝x2﹣2x，其顶点为A．
（1）写出这条抛物线的开口方向、顶点A的坐标，并说明它的变化情况；
（2）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”，试求抛物线y＝x2﹣2x的“不动点”的坐标．
20．如图，⊙O是四边形ABCD的外接圆，对角线AC与BD相交于点E，且AE＝DE，连接AD、CB．
（1）求证：AB＝CD；
（2）在不添加任何辅助线的情况下，直接写出图中所有的全等三角形．

21．中秋节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：
小王：该水果的进价是每千克22元；
小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低1元，每天的销售量将增加40千克．
根据他们的对话，解决下面所给问题：设降价x（x＞0）元，每天所获得的利润为w元．
（1）超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？
（2）这种水果的销售价定为多少时，可使每天销售利润最大？最大的利润是多少？
22．现要修建一条隧道，其截面为抛物线型，如图所示，线段OE表示水平的路面，以O为坐标原点，以OE所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系．根据设计要求：OE＝10m，该抛物线的顶点P到OE的距离为9m．
（1）求满足设计要求的抛物线的函数表达式；
（2）现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯．已知点A、B到OE的距离均为6m，求点A、B的坐标．

23．【问题提出】
（1）如图1，将正方形纸片ABCD折叠，使边AB、AD都落在对角线AC上，展开得到折痕AE、AF，连接EF，则∠EAF的度数为 　 　；
【问题解决】
（2）如图2，在正方形ABCD中，点E、F分别在边BC、CD上，保持∠EAF的度数不变，将△ADF绕着点A顺时针旋转90°，得到△ABG，请写出EF、DF、BE之间的数量关系，并说明理由；
（3）保持∠EAF的度数不变，将图3中的正方形纸片沿对角线BD剪开得到图4，请直接写出BM、DN、MN之变间的数量关系．




参考答案
一、选择题（每小题3分，共30分）
1．下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
解：A、不是轴对称图形，是中心对称图形，故此选项不合题意；
B、是轴对称图形，不是中心对称图形，故此选项不合题意；
C、既是轴对称图形又是中心对称图形，故此选项符合题意；
D、既不是轴对称图形，也不是中心对称图形，故此选项不合题意；
故选：C．
【点评】此题主要考查了轴对称图形和中心对称图形，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
2．一元二次方程2x2﹣5x+6＝0的根的情况为（　　）
A．无实数根 B．有两个不等的实数根
C．有两个相等的实数根 D．不能判定
【分析】求出判别式Δ＝b2﹣4ac，判断其的符号就即可得出结论．
解：∵Δ＝（﹣5）2﹣4×2×6＝25﹣48＝﹣23＜0，
∴2x2﹣5x+6＝0无实数根，
故选：A．
【点评】本题主要考查了一元二次方程根的判别式，掌握一元二次方程根的判别式Δ＜0时，方程无实数根是解决问题的关键．
3．点P（2，﹣1）关于原点对称的点P′的坐标是（　　）
A．（﹣2，1） B．（﹣2，﹣1） C．（﹣1，2） D．（1，﹣2）
【分析】根据关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反可直接写出答案．
解：点P（2，﹣1）关于原点对称的点P′的坐标是（﹣2，1），
故选：A．
【点评】此题主要考查了关于原点对称的点的坐标特点，关键是掌握点的坐标的变化规律．
4．如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB＝4，AC＝3，BC＝2，则BE的长为（　　）

A．5 B．4 C．3 D．2
【分析】根据旋转的性质可得AB＝AE，∠BAE＝60°可得△ABE是等边三角形．可得BE的长
解：∵将△ABC绕点A顺时针旋转60°得到△AED
∴∠BAE＝60°，BA＝AE
∴△ABE是等边三角形
∴BE＝AB＝4
故选：B．
【点评】本题考查旋转的性质，等边三角形的判定，本题关键是熟练掌握旋转图形的性质．
5．若二次函数y＝2x2﹣3的图象上有两个点A（1，a），B（2，b），则a与b的大小关系（　　）
A．a＞b B．a＝b C．a＜b D．无法确定
【分析】由抛物线解析式可得抛物线开口方向及对称轴，根据点A，B到对称轴的距离大小关系求解．
解：∵y＝2x2﹣3，
∴抛物线开口向上，对称轴为y轴，
∵1＜2，
∴a＜b．
故选：C．
【点评】本题考查二次函数图象上点的坐标特征，解题关键是掌握二次函数图象与系数的关系，掌握二次函数与不等式的关系．
6．一条排水管的截面如图所示，已知排水管的半径OB＝10，水面宽AB＝16，则截面圆心O到水面的距离OC是（　　）

A．4 B．5 C．6 D．6
【分析】根据垂径定理求出BC，根据勾股定理求出OC即可．
解：∵OC⊥AB，OC过圆心O点，
∴BC＝AC＝AB＝×16＝8，
在Rt△OCB中，由勾股定理得：OC＝＝＝6，
故选：D．
【点评】本题考查了勾股定理和垂径定理的应用；由垂径定理求出BC是解决问题的关键．
7．随着生产技术的进步，某制药厂生产成本逐年下降．两年前生产一吨药的成本是5000元，现在生产一吨药的成本是4050元．设生产成本的年平均下降率为x，下面所列方程正确的是（　　）
A．5000（1+x）2＝4050 B．4050（1+x）2＝5000
C．5000（1﹣x）2＝4050 D．4050（1﹣x）2＝5000
【分析】等量关系为：2年前的生产成本×（1﹣下降率）2＝现在的生产成本，把相关数值代入计算即可．
解：设这种药品成本的年平均下降率是x，根据题意得：
5000（1﹣x）2＝4050，
故选：C．
【点评】此题考查了由实际问题抽象出一元二次方程，平均增长率问题，一般形式为a（1+x）2＝b，a为起始时间的有关数量，b为终止时间的有关数量．
8．如果将抛物线y＝2x2先向左平移2个单位，再向上平移3个单位后得到一条新的抛物线，这条新的抛物线的表达式是（　　）
A．y＝2（x﹣2）2+3 B．y＝2（x+2）2﹣3
C．y＝2（x﹣2）2﹣3 D．y＝2（x+2）2+3
【分析】按照“左加右减，上加下减”的规律，即可得出平移后抛物线的解析式．
解：抛物线y＝2x2先向左平移2个单位得到解析式：y＝2（x+2）2，再向上平移3个单位得到抛物线的解析式为：y＝2（x+2）2+3．
故选：D．
【点评】此题考查了二次函数图象与几何变换，掌握抛物线解析式的变化规律：左加右减，上加下减是解题的关键．
9．如果一元二次方程ax2+bx+c＝0有两个根为x1，x2，那么方程的两个根x1，x2和系数a，b，c有如下关系：x1+x2＝﹣，x1x2＝．若m，n是方程x2+2x﹣2024＝0的两根，则2m﹣mn+2n＝（　　）
A．2020 B．﹣2028 C．﹣2020 D．2024
【分析】由根与系数的关系可得m+n＝﹣2，mn＝﹣2024，再整体代入运算即可．
解：∵m，n是方程x2+2x﹣2024＝0的两根，
∴m+n＝﹣2，mn＝﹣2024，
∴2m﹣mn+2n
＝2（m+n）﹣mn
＝2×（﹣2）﹣（﹣2024）
＝﹣4+2024
＝2020．
故选：A．
【点评】本题主要考查根与系数的关系，解答的关键是熟记根与系数的关系：x1+x2＝﹣，x1x2＝．
10．如图，一段抛物线y＝﹣x2+6x（0≤x≤6），记为抛物线C1，它与x轴交于点O、A1；将抛物线C1绕点A1旋转180°得抛物线C2，交x轴于点A2；将抛物线C2绕点A2，旋转180°得抛物线C3，交x轴于点A3；……如此进行下去，得到一条“波浪线”，若点M（17，m）在此“波浪线”上，则m的值为（　　）

A．﹣6 B．5 C．﹣4 D．0
【分析】根据y＝﹣x2+6x（0≤x≤6）可以得到：整个函数图象每隔6×2＝12个单位长度，函数值就相等，而2021＝12×1+6，由此即可计算．
解：∵y＝﹣x2+6x＝﹣x（x﹣6）（0≤x≤6），
∴A1（6，0），
∴整个函数图象每隔6×2＝12个单位长度，函数值就相等，
∵18＝12×1+6，
所以m的值等于x＝6时的纵坐标，
所以m＝﹣6×（6﹣6）＝0．
故选：D．
【点评】本题考查了抛物线与x轴的交点，二次函数的性质，二次函数与几何变换，解决此题的关键在于能根据函数图象发现规律：m的值等于x＝6时的纵坐标．
二、填空题（每小题3分，共15分）
11．已知x＝1是方程x2+ax+3＝0的一个根，则a的值为　﹣4　．
【分析】一元二次方程的根就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
解：把x＝1代入方程x2+ax+3＝0得1+a+3＝0，即a＝﹣4．
故答案是：﹣4．
【点评】本题主要考查了方程的解的定义，把求未知系数的问题转化为方程求解的问题．
12．如图，AB是半圆O的直径，点C，D在半圆上，若∠D＝120°，则∠B的度数是 　60°　．

【分析】利用圆内接四边形的性质求解即可．
解：∵四边形ABCD是圆内接四边形，
∴∠D+∠B＝180°，
∵∠D＝120°，
∴∠B＝60°，
故答案为：60°．
【点评】本题考查圆内接四边形的性质，解题的关键是记住圆内接四边形的对角互补．
13．已知二次函数y＝x2﹣2x+m的部分图象如图所示，则关于x的一元二次方程x2﹣2x+m＝0的解为　x1＝﹣1，x2＝3　．

【分析】求得抛物线与x轴的交点坐标，交点的横坐标就是方程的解．
解：（3，0）关于x＝1的对称点是（﹣1，0）．
则一元二次方程x2﹣2x+m＝0的解为x1＝﹣1，x2＝3．
故答案是：x1＝﹣1，x2＝3．
【点评】本题考查了抛物线与x轴的交点，与x轴交点的横坐标就是令y＝0所得方程的解．
14．如图，在一块长22m，宽为14m的矩形空地内修建三条宽度相等的小路，其余部分种植花草．若花草的种植面积为240m2，则小路宽为 　2　m．

【分析】设小路宽为xm，则种植花草部分的面积等同于长（22﹣x）m，宽（14﹣x）m的矩形的面积，根据花草的种植面积为240m2，即可得出关于x的一元二次方程，解之取其符合题意的值即可得出结论．
解：设小路宽为xm，则种植花草部分的面积等同于长（22﹣x）m，宽（14﹣x）m的矩形的面积，
依题意得：（22﹣x）（14﹣x）＝240，
整理得：x2﹣36x+68＝0，
解得：x1＝2，x2＝34（不符合题意，舍去）．
故答案为：2．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
15．AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q．若AB＝2，则线段BQ的长为　　．

【分析】连接AQ，BQ，根据圆周角定理可得出∠QAB＝∠P＝45°，∠AQB＝90°，故△ABQ是等腰直角三角形，根据勾股定理即可得出结论．
解：连接AQ，BQ，
∵∠P＝45°，
∴∠QAB＝∠P＝45°，
∵AB为直径，
∴∠AQB＝90°，
∴△ABQ是等腰直角三角形．
∵AB＝2，
∴2BQ2＝4，
∴BQ＝．
故答案为：．

【点评】本题考查的是圆周角定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
三、解答题（共75分）
16．用适当的方法解方程：
（1）x2﹣x﹣20＝0；
（2）5x2﹣3x﹣＝x2﹣3x+．
【分析】（1）利用因式分解法把方程转化为x﹣5＝0或x+4＝0，然后解一次方程即可；
（2）先把方程化为一般式，再利用因式分解法把方程转化为2x﹣1＝0或2x+1＝0，然后解一次方程即可．
解：（1）x2﹣x﹣20＝0，
（x﹣5）（x+4）＝0，
x﹣5＝0或x+4＝0，
所以x1＝5，x2＝﹣4；
（2）5x2﹣3x﹣＝x2﹣3x+，
4x2﹣1＝0，
（2x﹣1）（2x+1）＝0，
2x﹣1＝0或2x+1＝0，
所以x1＝，x2＝﹣．
【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
17．已知：关于x的一元二次方程2x2﹣3x+k＝0有两个不相等的实数根．
（1）求k的取值范围；
（2）当k取最大整数值时，求该方程的解．
【分析】（1）由方程根的情况可得到关于k的不等式，可求得k的取值范围；
（2）根据k的取值范围可求k值，解方程即可．
解：（1）∵关于x的一元二次方程2x2﹣3x+k＝0有两个不相等的实数根，
∴Δ＝（﹣3）2﹣4×2k＞0，
解得k＜；
（2）∵k＜，
∴k的最大整数值为1，
∴原方程为2x2﹣3x+1＝0，
∴（2x﹣1）（x﹣1）＝0，
∴2x﹣1＝0，x﹣1＝0，
∴x1＝，x2＝1．
【点评】本题考查了根的判别式和一元二次方程的解法，熟知一元二次方程ax2+bx+c＝0（a≠0）中，当Δ＞0时，方程有两个不相等的两个实数根是解答此题的关键．
18．如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上．
（1）将△ABC向左平移6个单位长度得到△A1B1C1，请画出△A1B1C1；
（2）画出△A1B1C1关于点O的中心对称图形△A2B2C2；
（3）若将△ABC绕某一点旋转可得到△A2B2C2那么旋转中心的坐标为 　（3，0）　，旋转角度为 　180　°．

【分析】（1）利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可；
（2）利用中心对称变换的性质分别作出A1，B1，C1的对应点A2，B2，C2；
（3）两个三角形成中心对称，对应点连线的交点即为旋转中心．
解：（1）如图，△A1B1C1即为所求；
（2）如图，△A2B2C2即为所求；
（3）若将△ABC绕某一点旋转可得到△A2B2C2那么旋转中心Q的坐标为（3，0），旋转角度为180°，
故答案为：（3，0），180．

【点评】本题考查作图﹣旋转变换，平移变换等知识，解题的关键是掌握旋转变换的性质，平移变换的性质，属于中考常考题型．
19．已知抛物线y＝x2﹣2x，其顶点为A．
（1）写出这条抛物线的开口方向、顶点A的坐标，并说明它的变化情况；
（2）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”，试求抛物线y＝x2﹣2x的“不动点”的坐标．
【分析】（1）a＝1＞0，故该抛物线开口向上，顶点A的坐标为（1，﹣1）；
（2）设抛物线“不动点”坐标为（t，t），则t＝t2﹣4t，即可求解．
解：（1）y＝x2﹣2x＝（x﹣1）2﹣1，
∵a＝1＞0，
∴故该抛物线开口向上，
顶点A的坐标为（1，﹣1），
当x＞1，y随x的增大而增大，当x＜1，y随x增大而减小；
（2）设抛物线“不动点”坐标为（t，t），则t＝t2﹣2t，
解得：t＝0或3，
故“不动点”坐标为（0，0）或（3，3）．
【点评】本题为二次函数综合运用题，涉及到二次函数基本知识，新定义问题，通常按照题设顺序，逐次求解即可．
20．如图，⊙O是四边形ABCD的外接圆，对角线AC与BD相交于点E，且AE＝DE，连接AD、CB．
（1）求证：AB＝CD；
（2）在不添加任何辅助线的情况下，直接写出图中所有的全等三角形．

【分析】（1）根据圆周角定理得到：∠AOB＝∠DOC，则由圆心角、弧，弦的关系证得结论；
（2）根据全等三角形的判定定理解答．
【解答】（1）证明：如图，连接OA、OB、OC、OD，
∵AE＝DE，
∴∠ADB＝∠DAC，
∴∠AOB＝∠DOC，
∴AB＝CD；

（2）解：①在△ABD与△DCA中，
．
故△ABD≌△DCA（AAS）；
②在△ABE与△DCE中，
．
故△ABE≌△DCE（AAS）；
③由AB＝DC知，∠ACB＝∠DBC．
在△ABC与△DCB中，
．
故△ABC≌△DCB（AAS）．

【点评】考查了圆心角、弧，弦的关系，全等三角形的判定，全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．
21．中秋节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：
小王：该水果的进价是每千克22元；
小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低1元，每天的销售量将增加40千克．
根据他们的对话，解决下面所给问题：设降价x（x＞0）元，每天所获得的利润为w元．
（1）超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？
（2）这种水果的销售价定为多少时，可使每天销售利润最大？最大的利润是多少？
【分析】（1）设降低x元，超市每天可获得销售利润3640元，由题意列出一元二次方程，解之即可得出答案；
（2）设降低x元，根据题意得到y＝﹣40x2+480x+2560，根据二次函数的性质即可得到结论．
解：（1）设降低x元，超市每天可获得销售利润3640元，由题意得，
（38﹣x﹣22）（160+×120）＝3640，
整理得x2﹣12x+27＝0，
∴x＝3或x＝9．
∵要尽可能让顾客得到实惠，
∴x＝9，
∴售价为38﹣9＝29（元），
答：水果的销售价为每千克29元时，超市每天可获得销售利润3640元；
（2）设降低x元，由题得y＝（38﹣x﹣22）（160+×120），
∴y＝﹣40x2+480x+2560＝﹣40（x﹣6） 2+4000，
当x＝6时，y最大＝4000．
∴售价为38﹣6＝32（元），
答：水果的销售价为每千克32元时，超市每天一天获利最大为4000元．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
22．现要修建一条隧道，其截面为抛物线型，如图所示，线段OE表示水平的路面，以O为坐标原点，以OE所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系．根据设计要求：OE＝10m，该抛物线的顶点P到OE的距离为9m．
（1）求满足设计要求的抛物线的函数表达式；
（2）现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯．已知点A、B到OE的距离均为6m，求点A、B的坐标．

【分析】（1）设抛物线的解析式为y＝a（x﹣5）2+9，把（0，0）代入，可得a＝﹣，即可解决问题；
（2）把y＝6，代入抛物线的解析式，解方程可得结论．
解：（1）由题意抛物线的顶点P（5，9），
∴可以假设抛物线的解析式为y＝a（x﹣5）2+9，
把（0，0）代入，可得a＝﹣，
∴抛物线的解析式为y＝﹣（x﹣5）2+9；

（2）令y＝6，得﹣（x﹣5）2+9＝6，
解得x1＝+5，x2＝﹣+5，
∴A（5﹣，6），B（5+，6）．
【点评】本题考查二次函数的应用，待定系数法，一元二次方程等知识，解题的关键是熟练掌握待定系数法，属于中考常考题型．
23．【问题提出】
（1）如图1，将正方形纸片ABCD折叠，使边AB、AD都落在对角线AC上，展开得到折痕AE、AF，连接EF，则∠EAF的度数为 　45°　；
【问题解决】
（2）如图2，在正方形ABCD中，点E、F分别在边BC、CD上，保持∠EAF的度数不变，将△ADF绕着点A顺时针旋转90°，得到△ABG，请写出EF、DF、BE之间的数量关系，并说明理由；
（3）保持∠EAF的度数不变，将图3中的正方形纸片沿对角线BD剪开得到图4，请直接写出BM、DN、MN之变间的数量关系．


【分析】（1）由四边形ABCD是正方形得∠BAD＝90°，由折叠得∠CAE＝∠BAC，∠CAF＝∠DAC，所以∠EAF＝∠BAC+∠DAC＝45°；
（2）由四边形ABCD是正方形，得AD＝AB，∠D＝∠ABE＝∠BAD＝90°，由旋转得BG＝DF，AG＝AF，∠ABG＝∠D＝90°，∠BAG＝∠DAF，则点G、B、E在同一条直线上，再证明△EAG≌△EAF，则EG＝EF，所以BE+DF＝BE+BG＝EG＝EF；
（3）将△ADN绕点A顺时针旋转90°，得到△ABH，连接MH，则BH＝DN，先证明∠MBH＝∠ABD+∠ABH＝90°，则BM2+BH2＝MH2，再证明△MAH≌△MAN，得MH＝MN，则BM2+DN2＝MN2．
解：（1）如图1，∵四边形ABCD是正方形，
∴∠BAD＝90°，
由折叠得∠CAE＝∠BAE＝∠BAC，∠CAF＝∠DAF＝∠DAC，
∴∠EAF＝∠CAE+∠CAF＝∠BAC+∠DAC＝∠BAD＝45°，
故答案为：45°；
（2）BE+DF＝EF，理由如下：
如图2，∵四边形ABCD是正方形，
∴AD＝AB，∠D＝∠ABE＝∠BAD＝90°，
由旋转得BG＝DF，AG＝AF，∠ABG＝∠D＝90°，∠BAG＝∠DAF，
∴∠ABE+∠ABG＝180°，
∴点G、B、E在同一条直线上，
∵∠EAF＝45°，
∴∠EAG＝∠BAE+∠BAG＝∠BAE+∠DAF＝90°﹣∠EAF＝45°，
∴∠EAG＝∠EAF，
∵AE＝AE，
∴△EAG≌△EAF（SAS），
∴EG＝EF，
∵BE+DF＝BE+BG＝EG，
∴BE+DF＝EF；
（3）BM2+DN2＝MN2，证明如下：
如图4，将△ADN绕点A顺时针旋转90°，得到△ABH，连接MH，
∵AB＝AD，∠BAD＝90°，
∴∠ABD＝∠D＝45°，
由旋转得∠ABH＝∠D＝45°，BH＝DN，AH＝AN，∠BAH＝∠DAN，
∴∠MBH＝∠ABD+∠ABH＝90°，
∴BM2+BH2＝MH2，
∵∠MAN＝45°，
∴∠MAH＝∠BAM+∠BAH＝∠BAM+∠DAN＝90°﹣∠MAN＝45°，
∴∠MAH＝∠MAN，
∵AM＝AM，
∴△MAH≌△MAN（SAS），
∴MH＝MN，
∴BM2+DN2＝MN2．



【点评】此题考查正方形的性质，旋转的性质、等腰直角三角形的性质、全等三角形的判定与性质、勾股定理等知识，此题难度适中，正确地作出辅助线是解题的关键．