人教A版高一上南海区统考复习分段函数&函数图象(答案版)
展开
六、分段函数的计算题举例
(1)分段函数单调性求参问题
例1、已知函数是上的减函数,则实数的取值范围是______.
【详解】由题设在R上递减,结合一次函数和反比例函数性质,
所以,可得.故答案为:
(2)分段函数的作图及性质
例2、已知函数.
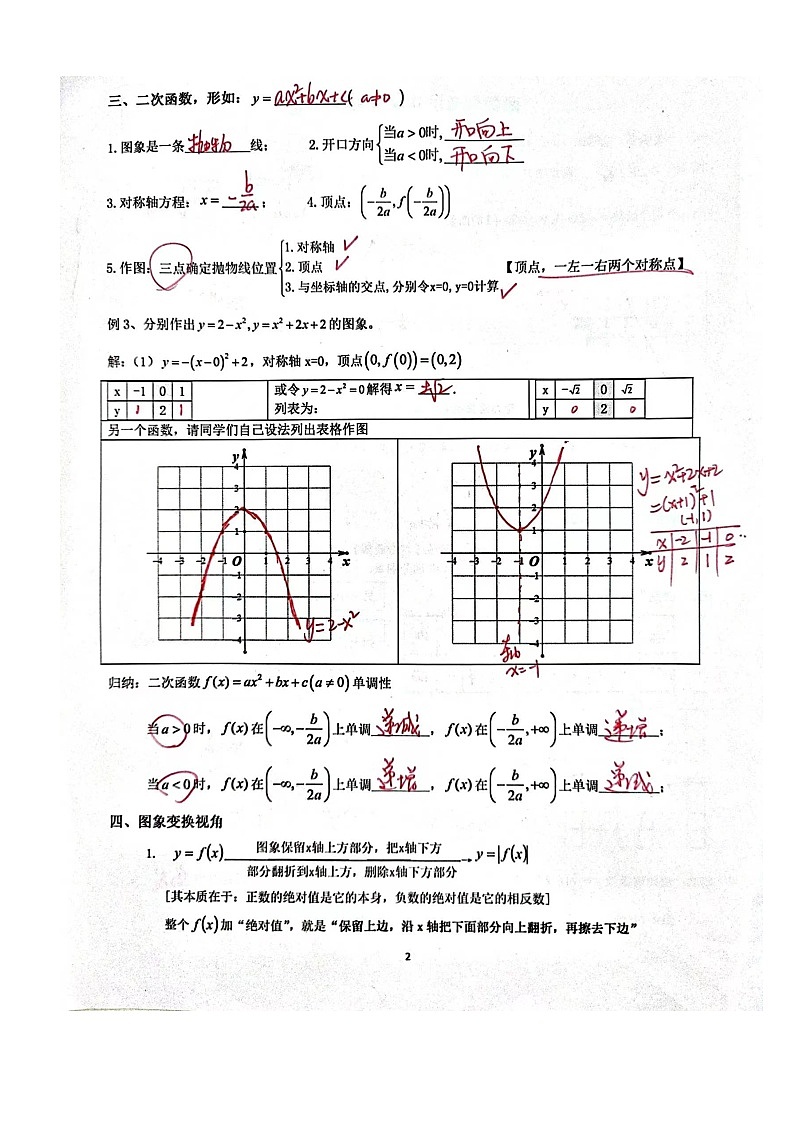
(1)画出函数的图象; (2)若,求其值域; (3)当时,求实数x的取值范围.
|
解:(1)时,函数为二次函数,当时,函数为一次函数,画出分段函数图象,注意一次函数与轴交点为空心;
(2)结合(1)中所画的函数图象,得到函数值域;
(3)分与两种情况,解不等式,求出实数x的取值范围.
(1)
(2)由(1)可知:当时,单调递减, 当时,单调递减,, 综上:函数的值域为; (3)当时,,解得:,与 求交集得:;当时,时,解得:,与取交集得:,综上:实数x的取值范围是. |
(3)分段函数的分类讨论计算问题
例3、已知函数 (1)求,,的值;
(2)若,求实数a的值; (3)若,求实数m的取值范围.
解:(1)由题可得,,
因为,所以;
(2)①当时,,解得,不合题意,舍去;
②当时,,即,解得或,
因为,,所以符合题意;
③当时,,解得,符合题意;
综合①②③知,当时,或;
(3)由,得或或,
解得或,故所求m的取值范围是.
习题
1、 已知函数是增函数,求实数a的取值范围。
解:由解得:
2、已知函数 ①求, ②若,求的值
【解】函数,①,.
②当时,,解得,成立;
当时,,解得或(舍);
当时,,解得(舍去).故的值为或1.
3、若定义运算a⊙b=则函数f(x)=x⊙(2-x)的值域是__________.
解:a⊙b=实质上是“取小”,画图象即得
f(x)=x⊙(2-x)==,
由图象可知:当x=1是
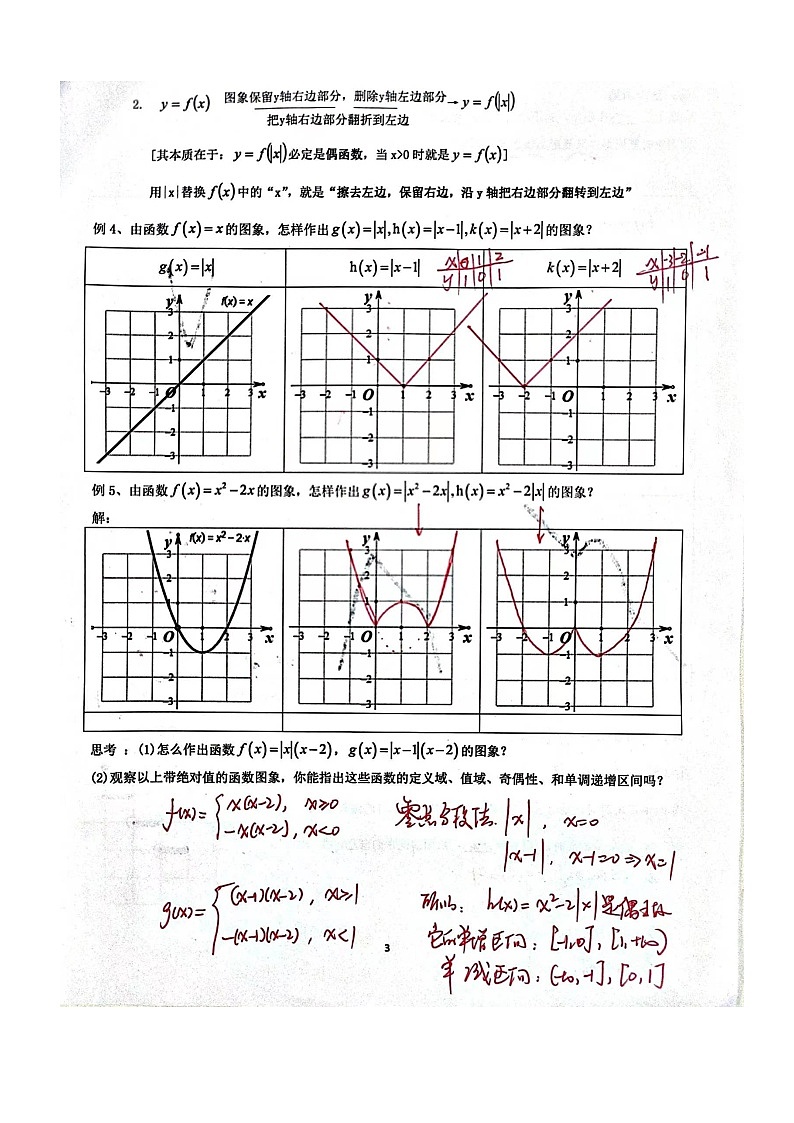
4、已知函数f(x)=-x2+2,g(x)=x,令φ(x)=min{f(x),g(x)}(即f(x)和g(x)中的较小者).
(1)分别用图象法和解析式表示φ(x);
(2)求函数φ(x)的定义域,值域.
解 (1)在同一个坐标系中画出函数f(x),g(x)的图象如图①.
由图①中函数取值的情况,结合函数φ(x)的定义,可得函数φ(x)的图象如图②.
令-x2+2=x得x=-2或x=1.
结合图②,得出φ(x)的解析式为φ(x)=
(2)由图②知,φ(x)的定义域为R,φ(1)=1,∴φ(x)的值域为(-∞,1].
5、(2020年南海区统考19)若函数f(x)=|x﹣2|.
(1)在给定的平面直角坐标系中画出函数f(x)图象;
(2)写出函数f(x)的值域、单调区间;
(3)在①,②x﹣3,③x+2这三个式子中任选出一个使其等于h(x),
求不等式f(x)>h(x)的解集.
解:(1)由f(x)=|x﹣2|=,图象如图所示;
(2)由图象可得函数的值域为[0,+∞),在(﹣∞,2)上为减函数,在[2,+∞)上为增函数;
(3)若选①,则|x﹣2|>x+2,即或,解得x>5或x<0,
即不等式的解集为(﹣∞,0)∪(5,+∞),
若选②,则|x﹣2|>x﹣3,即或,
解得x≥2或x<2,即不等式的解集为R,
若选③,|x﹣2|>x+2,即或,
解得x<2,即不等式的解集为(﹣∞,2).
(课本P102,T13:2020年南海区统考考过) |
解:(1)当0<t≤1时,2 (1分)
当1<t≤2时, 当t>2时,
所以
(2)画图象,如图:(其中图形,规范1分)
(3)当0<t≤1时,,由,解得
因为0<t≤1,所以,即
当时,直线y=at过点,这两点都在f(t)的图象上
当时,直线y=at与射线有一个交点
当1<t≤2时,直线y=a()逆时针旋转时与f(t)图象有两个交点,相切时有一个交点,且与射线无交点.此时,所以 ,
所以,解得或.
当时,,所以在(1,2]内.
当.时不在(1,2]内,
当a≤0或a时,直线y=at与f(t)的图象无交点,所以.
7、已知函数的最小值为.
(1)求的值; (2)若,,且,求的最小值.
解:(1)由题可得,然后根据函数的单调性进而即得;
(2)由题可得,然后根据基本不等式即得.
(1)由题意可得,
则在上单调递减,在上单调递增,故,即;
(2)由(1)可知,则,因为,
所以,因为,
所以,当且仅当时,等号成立,即的最小值为.
人教A版高一上数学 南海区统考复习分段函数&函数图象(学生版): 这是一份人教A版高一上数学 南海区统考复习分段函数&函数图象(学生版),共6页。学案主要包含了一次函数,形如,反比例函数,形如,二次函数,形如,图象变换视角,分段函数,分段函数的计算题举例等内容,欢迎下载使用。
高中人教B版 (2019)第四章 指数函数、对数函数与幂函数4.2 对数与对数函数4.2.3 对数函数的性质与图像学案设计: 这是一份高中人教B版 (2019)第四章 指数函数、对数函数与幂函数4.2 对数与对数函数4.2.3 对数函数的性质与图像学案设计,共11页。学案主要包含了课程标准等内容,欢迎下载使用。
高中数学第五章 三角函数5.4 三角函数的图象与性质学案设计: 这是一份高中数学第五章 三角函数5.4 三角函数的图象与性质学案设计,共13页。