人教A版高一上数学 南海区统考复习分段函数&函数图象（学生版）

这是一份人教A版高一上数学 南海区统考复习分段函数&函数图象（学生版），共6页。学案主要包含了一次函数，形如，反比例函数，形如，二次函数，形如，图象变换视角，分段函数，分段函数的计算题举例等内容，欢迎下载使用。
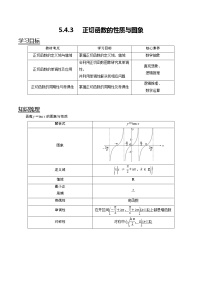
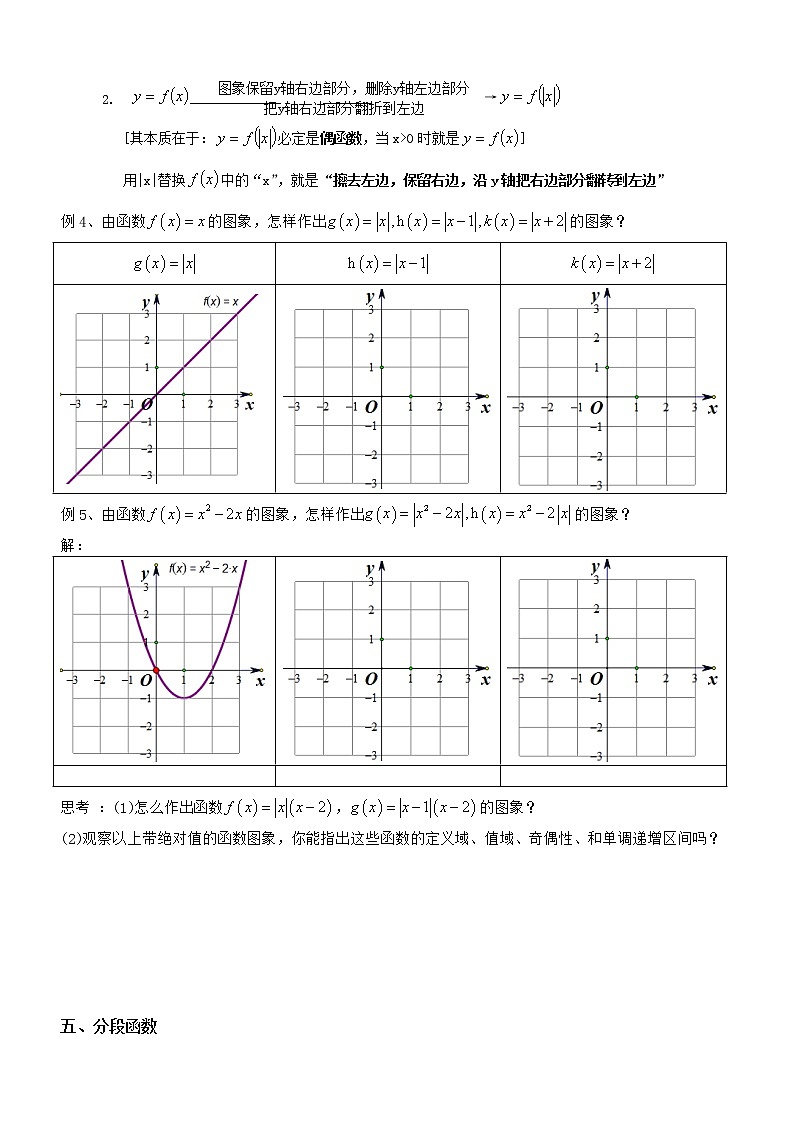
函数图象与分段函数一、一次函数，形如：图象是一条_______.    两点确定一条直线，只要“两点”就够都可以呀。例1：分别作函数的图象。注意：当k=0时，函数变为常数函数y=b，它的图象是一条__________的直线。归纳：一次函数单调性，当时，为单调____函数；当时，为单调____函数；二、反比例函数，形如：定义域是_____________；该函数是一个____函数【填奇或偶】，图象关于_______对称；图象是两支___________；由对称性，先作出x>0部分图象，再由对称性即可作出另一半图象例2、分别作出的图象，x…1234…100           归纳：反比例函数单调性：当时，在上都单调_________；当时，在上都单调_________；三、二次函数，形如：1.图象是一条__________线；     2.开口方向3.对称轴方程：；     4.顶点：5.作图：三点确定抛物线位置【顶点，一左一右两个对称点】例3、分别作出的图象。解：（1），对称轴x=0，顶点x-101y 2 或令解得.列表为：x-0y 2 另一个函数，请同学们自己设法列出表格作图归纳：二次函数单调性当时，在上单调_________，在上单调_________；当时，在上单调_________，在上单调_________；四、图象变换视角[其本质在于：正数的绝对值是它的本身，负数的绝对值是它的相反数]整个加“绝对值”，就是“保留上边，沿x轴把下面部分向上翻折，再擦去下边”[其本质在于：必定是偶函数，当x>0时就是]用|x|替换中的“x”，就是“擦去左边，保留右边，沿y轴把右边部分翻转到左边”例4、由函数的图象，怎样作出的图象？例5、由函数的图象，怎样作出的图象？解：   思考 ：(1)怎么作出函数，的图象？(2)观察以上带绝对值的函数图象，你能指出这些函数的定义域、值域、奇偶性、和单调递增区间吗？        五、分段函数实质上是_____个函数，只不过是不同的定义域范围有着不同的_____________。作图象时要记得“只要定义域之内的部分，擦去定义域之外的部分”。 例6、作下列分段函数的图象（如需列表，自己在草稿上列表）（段测题）函数有最大值，最小值吗？函数有最大值是多少？函数的值域是什么？例7、高斯函数表示函数值不超过x的最大整数，例如：当时，写出的解析式，并作出的函数图象。解：当时，；后面请同学们自己完成    六、分段函数的计算题举例（1）分段函数单调性求参问题例1、已知函数是上的减函数，则实数的取值范围是______.     （2）分段函数的作图及性质例2、已知函数.(1)画出函数的图象；(2)若，求其值域；(3)当时，求实数x的取值范围.  （3）分段函数的分类讨论计算问题例3、已知函数，(1)求，，的值；     (2)若，求实数a的值；    (3)若，求实数m的取值范围．   习题1、 已知函数是增函数，求实数a的取值范围。2、已知函数      ①求，      ②若，求的值 3、若定义运算a⊙b＝则函数f(x)＝x⊙(2－x)的值域是__________． 4、已知函数f(x)＝－x2＋2，g(x)＝x，令φ(x)＝min{f(x)，g(x)}(即f(x)和g(x)中的较小者).(1)分别用图象法和解析式表示φ(x)；(2)求函数φ(x)的定义域，值域． 5、（2020年南海区统考19）若函数f（x）＝|x﹣2|．（1）在给定的平面直角坐标系中画出函数f（x）图象；（2）写出函数f（x）的值域、单调区间；（3）在①，②x﹣3，③x+2这三个式子中任选出一个使其等于h（x），求不等式f（x）＞h（x）的解集．    （课本P102，T13：2020年南海区统考考过） 7、已知函数的最小值为.(1)求的值；(2)若，，且，求的最小值.