- 3.1.2 函数的表示方法 教案 教案 1 次下载
- 3.1.3 函数的单调性 教案 教案 1 次下载
- 3.2.2 一次函数模型 教案 教案 0 次下载
- 3.2.3 二次函数模型 教案 教案 0 次下载
- 3.2.3 函数的应用 教案 教案 0 次下载
中职数学人教版(中职)基础模块上册3.2 一次函数和二次函数教案
展开3.2.1 一次、二次问题
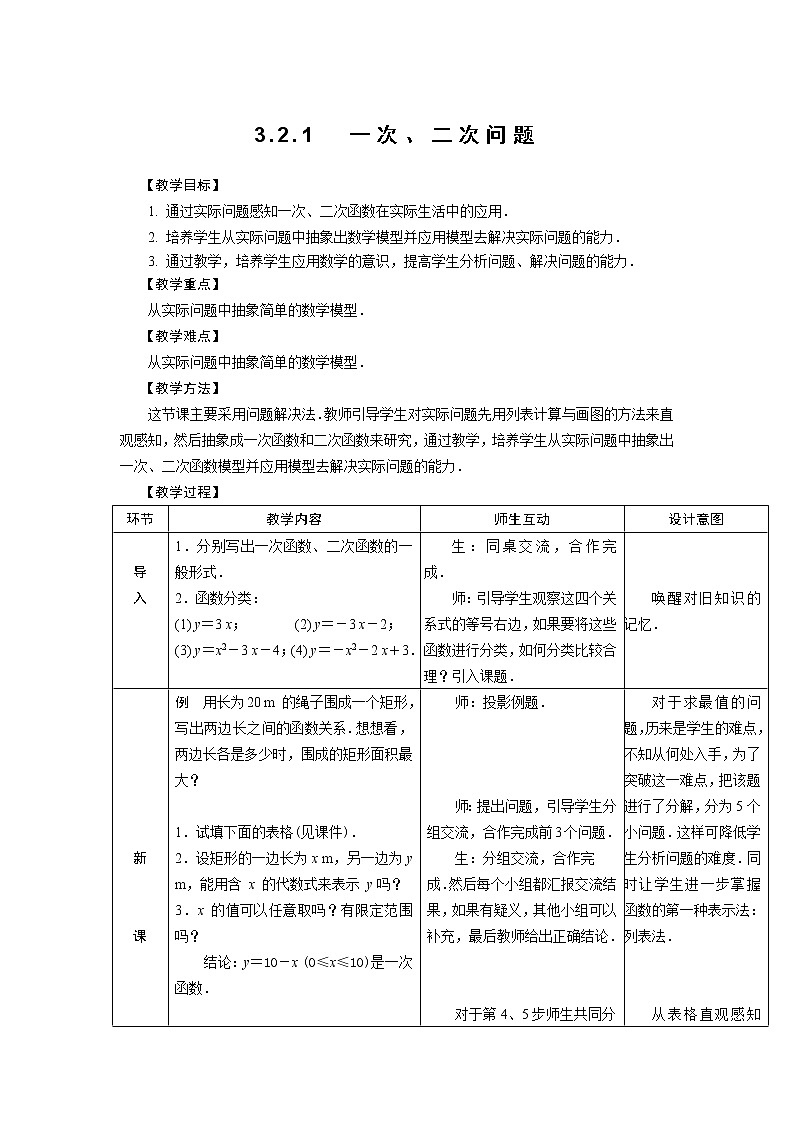
【教学目标】
1. 通过实际问题感知一次、二次函数在实际生活中的应用.
2. 培养学生从实际问题中抽象出数学模型并应用模型去解决实际问题的能力.
3. 通过教学,培养学生应用数学的意识,提高学生分析问题、解决问题的能力.
【教学重点】
从实际问题中抽象简单的数学模型.
【教学难点】
从实际问题中抽象简单的数学模型.
【教学方法】
这节课主要采用问题解决法.教师引导学生对实际问题先用列表计算与画图的方法来直观感知,然后抽象成一次函数和二次函数来研究,通过教学,培养学生从实际问题中抽象出一次、二次函数模型并应用模型去解决实际问题的能力.
【教学过程】
环节 | 教学内容 | 师生互动 | 设计意图 |
导 入 | 1.分别写出一次函数、二次函数的一般形式. 2.函数分类: (1) y=3 x; (2) y=-3 x-2; (3) y=x2-3 x-4;(4) y=-x2-2 x+3. | 生:同桌交流,合作完成. 师:引导学生观察这四个关系式的等号右边,如果要将这些函数进行分类,如何分类比较合理?引入课题. | 唤醒对旧知识的记忆. |
新
课
新
课
新
课 | 例 用长为20 m 的绳子围成一个矩形,写出两边长之间的函数关系.想想看,两边长各是多少时,围成的矩形面积最大?
1.试填下面的表格(见课件). 2.设矩形的一边长为 x m,另一边为 y m,能用含 x 的代数式来表示 y吗? 3.x 的值可以任意取吗?有限定范围吗? 结论:y=10-x (0≤x≤10)是一次函数.
4.又设矩形的面积为 S,我们发现S 是 x 的函数,试写出这个函数的关系式. 5.从表中得出 x(x 为整数)为多长时,矩形面积获得最大值?
6.作函数图象,从图象中求出当x为何值时,面积有最大值. 基本步骤:列表、描点、连线.
结论: 当矩形的一边小于5 m 时,函数值随边长增加而增加; 当矩形的一边等于5 m 时,矩形面积获得最大值; 当矩形的一边大于5 m 时,函数值随边长增加而减小. 7.用配方法分析,当x为何值时,面积有最大值. S=x(10-x) =-x2+10 x =-(x2-10 x) =-(x2-10 x+25-25) =-[(x-5)2-25] =-(x-5)2+25. 所以当 x=5时,矩形面积获得最大值. 结论: S=a(x+)2+. 当 x=- 时,函数有最值.
练习1 求自变量 x 为何值时,函数取得最大值或最小值? (1) f (x)=-x2+3; (2) f (x)=-x2-8; (3) f (x)=x2-5; (4) f (x)=-(x-5)2-3.
练习2 求自变量x为何值时,函数取得最大值或最小值. (1) f (x)=x2-2 x-3; (2) f (x)=-x2+4 x-8. | 师:投影例题.
师:提出问题,引导学生分组交流,合作完成前3个问题. 生:分组交流,合作完成.然后每个小组都汇报交流结果,如果有疑义,其他小组可以补充,最后教师给出正确结论.
对于第4、5步师生共同分析,教师首先引导学生从表格中找到当 x=5时,矩形面积最大是25.
学生依据上面的表格画出函数的图象.
教师首先引导学生关注图象的最高点,得出 x=5时矩形面积最大是25.
教师进一步引导学生观察图象,得出函数值的变化趋势.
师生共同解决. 教师引导学生关注配方法的几个关键地方.
教师引导学生回忆得出二次函数配方后的形式.
学生抢答.
学生自行解决,教师巡视并加以指导,同时有两名学生板演. | 对于求最值的问题,历来是学生的难点,不知从何处入手,为了突破这一难点,把该题进行了分解,分为5个小问题.这样可降低学生分析问题的难度.同时让学生进一步掌握函数的第一种表示法:列表法.
从表格直观感知面积的最值.
从图象直观感知面积的最值.同时让学生进一步掌握函数的第二种表示法:图象法.培养学生细心观察、归纳、分析的良好习惯和读图能力.
从解析式直观感知面积的最值.同时让学生进一步掌握函数的第三种表示法:解析法. 培养学生用多种方法分析问题、解决问题的能力.
形式中当 x=- 时,函数有最值的理解是难点,此处的设计目的是为了突破学生这一思维障碍.加深对配方法的理解.
通过练习1、2,让学生逐步掌握利用配方法来研究二次函数.同时进一步培养学生细心观察、分析问题的能力.
|
小 结 | 1.进一步熟悉用列表、画图或公式来表示某个函数关系. 2.用配方法求自变量 x 为何值时,函数取得最值. | 学生阅读课本畅谈本节课的收获,老师引导梳理,总结本节课的知识点. | 梳理总结,也可针对学生薄弱或易错处进行强调和总结. |
作 业 | 教材 P77,练习A 组第1题; 练习B 组第 1、2(选做)题. |
| 巩固拓展. |
中职数学人教版(中职)基础模块上册3.1 函数精品教案: 这是一份中职数学人教版(中职)基础模块上册3.1 函数精品教案,共6页。教案主要包含了一次函数图像和性质等内容,欢迎下载使用。
中职数学高教版(2021)拓展模块一 上册第3章 圆锥曲线3.2 双曲线3.2.1 双曲线的标准方程获奖教案: 这是一份中职数学高教版(2021)拓展模块一 上册第3章 圆锥曲线3.2 双曲线3.2.1 双曲线的标准方程获奖教案,共10页。教案主要包含了设计意图等内容,欢迎下载使用。
【中职专用】高中数学 人教版2021·基础模块上册 3.2.1一次函数模型(教案): 这是一份【中职专用】高中数学 人教版2021·基础模块上册 3.2.1一次函数模型(教案),共6页。教案主要包含了一次函数图像和性质等内容,欢迎下载使用。












