广西贺州市昭平县2022-2023学年八年级上学期期中数学试卷(含答案)

这是一份广西贺州市昭平县2022-2023学年八年级上学期期中数学试卷(含答案)，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年广西贺州市昭平县八年级第一学期期中数学试卷
一、选择题（本大题12小题，每小题3分，满分36分；在每小题给出的四个选项中，只有一项是符合题意的，请将符合题意的字母序号填在题号的括号内）
1．若点P（﹣3，b）在第二象限内，则b可以是（　　）
A．﹣2 B．﹣1 C．0 D．2
2．如图，点M是平面直角坐标系中的一点，MA⊥x轴，垂足为A，MB⊥y轴，垂足为B，且MA＝4，MB＝3，点M的坐标为（　　）

A．（4，3） B．（3，4） C．（﹣3，4） D．（﹣4，3）
3．一次函数y＝kx+1（k＞0）的图象一定经过第（　　）
A．一、二象限 B．一、二、三象限
C．一、二、四象限 D．一、四象限
4．已知函数y＝（m+3）x+2是一次函数，则m的取值范围是（　　）
A．m≠﹣3 B．m≠1 C．m≠0 D．m≠3
5．某市出租车计费办法如图所示．根据图象信息，下列说法错误的是（　　）

A．出租车起步价是10元
B．在3千米内只收起步价
C．超过3千米部分（x＞3）每千米收3元
D．超过3千米时（x＞3）所需费用y与x之间的函数关系式是y＝2x+4
6．下列各点不在一次函数y＝2x﹣3的图象上的是（　　）
A．（0，﹣3） B． C．（1，2） D．（2，1）
7．在平面直角坐标系中，把点（2，﹣1）向右平移1个单位后所得的点的坐标是（　　）
A．（2，0） B．（2，﹣2） C．（1，﹣1） D．（3，﹣1）
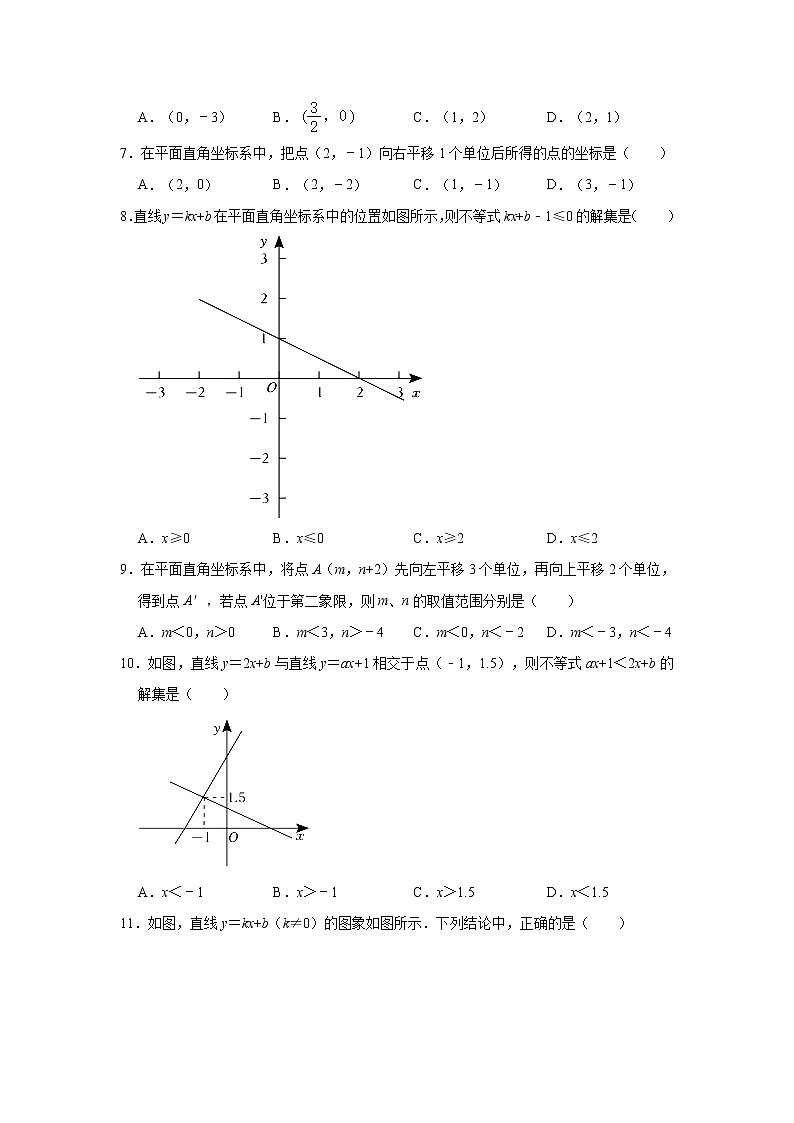
8．直线y＝kx+b在平面直角坐标系中的位置如图所示，则不等式kx+b﹣1≤0的解集是（　　）

A．x≥0 B．x≤0 C．x≥2 D．x≤2
9．在平面直角坐标系中，将点A（m，n+2）先向左平移3个单位，再向上平移2个单位，得到点A′，若点A'位于第二象限，则m、n的取值范围分别是（　　）
A．m＜0，n＞0 B．m＜3，n＞﹣4 C．m＜0，n＜﹣2 D．m＜﹣3，n＜﹣4
10．如图，直线y＝2x+b与直线y＝ax+1相交于点（﹣1，1.5），则不等式ax+1＜2x+b的解集是（　　）

A．x＜﹣1 B．x＞﹣1 C．x＞1.5 D．x＜1.5
11．如图，直线y＝kx+b（k≠0）的图象如图所示．下列结论中，正确的是（　　）

A．k＞0
B．方程kx+b＝0的解为x≠1
C．b＜0
D．若点A（1，m）、B（3，n）在该直线图象上，则m＞n
12．如图（1），在矩形ABCD中，动点P从点C出发，沿路线C→D→A做匀速运动，图（2）是此运动过程中，△PBC的面积S与点P运动的路程x之间的函数图象的一部分，则BC+CD的长为（　　）

A．5 B．6 C．7 D．12
二、填空题（本大题6小题，每小題3分，满分18分；请将答案直接写在题中的横线上）
13．若函数y＝x+k﹣2为正比例函数，则k的值为 　 　．
14．某工程队正在对一湿地公园进行绿化，中间休息了一段时间，已知绿化面积S（m2）与工作时间t（h）的函数关系的图象如图所示，则休息后工程队每小时绿化面积为 　 　m2．

15．如图，△ABC向右平移4个单位得到△A1B1C1，则点A1的坐标是 　 　．

16．如图，把直线y＝﹣2x向上平移后得到直线AB，直线AB经过点A（0，1），则直线AB的解析式是 　 　．

17．若点（m+1，2n﹣m）在x轴上，且到原点的距离为1，那么mn的值为 　 　．
18．如图，在△ABC中，AB＝2022，AC＝2019，AD为中线，则△ABD与△ACD的周长之差＝　 　．

三、解答题（本大题共8小题，满分66分；解答题应写出演算步骤或证明过程）
19．已知每千克化工原料的售价为120元，若x（元）表示购买m千克化工原料的总价钱．
（1）写出m与x的函数关系式；
（2）说出其中的变量与常量．
20．已知点P（x，y）满足3x﹣2y＝2，求P（2m+4，m﹣1）的坐标．
21．在平面直角坐标系中，点P的坐标为（a﹣7，3﹣2a），将点P向上平移4个单位，再向右平移5个单位后得到点Q．
（1）若点Q位于第一象限，求a的取值范围．
（2）在（1）的条件下，若a为整数，求出P、Q两点坐标．
22．如图，函数y＝2x和y＝ax+4的图象相交于点A（m，3）．
（1）求m，a的值；
（2）根据图象，直接写出不等式2x＞ax+4的解集．

23．如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AB＝13cm，BC＝12cm，AC＝5cm．
（1）求△ABC的面积；
（2）求CD的长．

24．Ⅰ号无人机从海拔10m处出发，以10m/min的速度匀速上升，Ⅱ号无人机从海拔30m处同时出发，以a（m/min）的速度匀速上升，经过tmin两架无人机位于同一海拔高度60m．无人机海拔高度y（m）与时间x（min）的关系如图．两架无人机都上升了20min．
（1）求t的值及Ⅱ号无人机海拔高度y（m）与时间x（min）的关系式；
（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高40米．

25．已知一次函数y＝kx+b（k≠0）的图象经过点（3，5）与（﹣4，﹣9）．
（1）求这个一次函数的解析式；
（2）判断点是否在这个一次函数的图象上；
（3）直接写出关于x的一元一次方程kx+b＝0的解．
26．为了抓住中秋商机，某商店计划购进A，B两种月饼，若购进A种月饼10盒，B种月饼5盒，需要600元；若购进A种月饼5盒，B种月饼3盒，需要330元．
（1）求购进A、B两种月饼每盒需要多少元？
（2）若该商店决定拿出2400元全部用来购进两种月饼，考虑市场需求，要求购进A种月饼的数量不少于B种月饼数量6倍，且不超过B种月饼数量的8倍．请你分别求出该商店共有几种进货方案？


参考答案
一、选择题（本大题12小题，每小题3分，满分36分；在每小题给出的四个选项中，只有一项是符合题意的，请将符合题意的字母序号填在题号的括号内）
1．若点P（﹣3，b）在第二象限内，则b可以是（　　）
A．﹣2 B．﹣1 C．0 D．2
【分析】根据点在第二象限内，横坐标小于零，纵坐标大于零即可判断．
解：∵点P（﹣3，b）在第二象限内，
∴b＞0，
∵﹣2＜0，﹣1＜0，0＝0，2＞0，
∴b可以为2，
故选：D．
【点评】本题考查了根据点的位置求点的坐标，解题关键在于能够熟记每个象限点的坐标特征．
2．如图，点M是平面直角坐标系中的一点，MA⊥x轴，垂足为A，MB⊥y轴，垂足为B，且MA＝4，MB＝3，点M的坐标为（　　）

A．（4，3） B．（3，4） C．（﹣3，4） D．（﹣4，3）
【分析】根据平面直角坐标系中点的坐标特征即可确定．
解：∵MA⊥x轴，垂足为A，MB⊥y轴，垂足为B，且MA＝4，MB＝3，
∴点M坐标为（﹣3，4），
故选：C．
【点评】本题考查了坐标与图形性质，熟练掌握平面直角坐标系中点的坐标特征是解题的关键．
3．一次函数y＝kx+1（k＞0）的图象一定经过第（　　）
A．一、二象限 B．一、二、三象限
C．一、二、四象限 D．一、四象限
【分析】根据b、k的符号确定函数的大致图象，即可求解．
解：当k＞0时，一次函数y＝kx+1（k≠0）的图象一定经过第一、二、三象限；
故选：B．
【点评】本题考查的是一次函数的性质，要求学生能根据k、b的符号，大致确定函数的图象，进而求解．
4．已知函数y＝（m+3）x+2是一次函数，则m的取值范围是（　　）
A．m≠﹣3 B．m≠1 C．m≠0 D．m≠3
【分析】根据一次函数的定义，可得m+3≠0，然后进行计算即可解答．
解：由题意得：
m+3≠0，
∴m≠﹣3，
故选：A．
【点评】本题考查了一次函数的定义，熟练掌握一次函数的定义是解题的关键．
5．某市出租车计费办法如图所示．根据图象信息，下列说法错误的是（　　）

A．出租车起步价是10元
B．在3千米内只收起步价
C．超过3千米部分（x＞3）每千米收3元
D．超过3千米时（x＞3）所需费用y与x之间的函数关系式是y＝2x+4
【分析】根据图象信息一一判断即可解决问题．
解：由图象可知，出租车的起步价是10元，在3千米内只收起步价，
设超过3千米的函数解析式为y＝kx+b，则，解得，
∴超过3千米时（x＞3）所需费用y与x之间的函数关系式是y＝2x+4，
超过3千米部分（x＞3）每千米收2元，
故A、B、D正确，C错误，
故选：C．
【点评】此题主要考查了一次函数的应用、学会待定系数法确定函数解析式，正确由图象得出正确信息是解题关键，属于中考常考题型，
6．下列各点不在一次函数y＝2x﹣3的图象上的是（　　）
A．（0，﹣3） B． C．（1，2） D．（2，1）
【分析】把选项中点的坐标分别代入函数解析式进行判断即可．
解：∵y＝2x﹣3，
∴当x＝0时，y＝0﹣3＝﹣3，故点（0，﹣3）在函数图象上，
当x＝时，y＝2×﹣3＝0，故点（，0）在函数图象上，
当x＝1时，y＝2×1﹣3＝﹣1≠2，故点（1，2）不在函数图象上，
当x＝2时，y＝2×2﹣3＝1，故点（2，1）在函数图象上，
故选：C．
【点评】本题主要考查一次函数图象上点的坐标特征，掌握函数图象上点的坐标满足函数解析式是解题的关键．
7．在平面直角坐标系中，把点（2，﹣1）向右平移1个单位后所得的点的坐标是（　　）
A．（2，0） B．（2，﹣2） C．（1，﹣1） D．（3，﹣1）
【分析】根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得答案．
解：平移后的坐标为（2+1，﹣1），即坐标为（3，﹣1），
故选：D．
【点评】此题主要考查了坐标与图形的变化﹣平移，关键是掌握平移规律．
8．直线y＝kx+b在平面直角坐标系中的位置如图所示，则不等式kx+b﹣1≤0的解集是（　　）

A．x≥0 B．x≤0 C．x≥2 D．x≤2
【分析】观察图象可得不等式的解集．
解：由不等式kx+b﹣1≤0得kx+b≤1．
观察图象，当x≥0时，y≤1，
即kx+b≤1．
所以不等式kx+b﹣1≤0的解集是x≥0．
故选：A．
【点评】本题主要考查了一次函数和一元一次不等式，掌握直线和y轴的交点的横坐标与不等式的解集的关系是解题的关键．
9．在平面直角坐标系中，将点A（m，n+2）先向左平移3个单位，再向上平移2个单位，得到点A′，若点A'位于第二象限，则m、n的取值范围分别是（　　）
A．m＜0，n＞0 B．m＜3，n＞﹣4 C．m＜0，n＜﹣2 D．m＜﹣3，n＜﹣4
【分析】根据第二象限点的特征，根据不等式组解决问题即可．
解：平移后的坐标为（m﹣3，n+4），
由题意，，
解得，
故选：B．
【点评】本题考查坐标与图形变化﹣平移，不等式组等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
10．如图，直线y＝2x+b与直线y＝ax+1相交于点（﹣1，1.5），则不等式ax+1＜2x+b的解集是（　　）

A．x＜﹣1 B．x＞﹣1 C．x＞1.5 D．x＜1.5
【分析】根据图象可以看出当x＞﹣1时，直线y＝2x+b在直线y＝ax+1的上方，即可得出答案．
解：由图象可知两直线交点是（﹣1，1.5），
当x＞﹣1时，直线y＝2x+b在直线y＝ax+1的上方，
即不等式ax+1＜2x+b的解集为：x＞﹣1，
故选：B．
【点评】本题考查的是一次函数与一元一次不等式，能利用数形结合求出不等式的解集是解答此题的关键．
11．如图，直线y＝kx+b（k≠0）的图象如图所示．下列结论中，正确的是（　　）

A．k＞0
B．方程kx+b＝0的解为x≠1
C．b＜0
D．若点A（1，m）、B（3，n）在该直线图象上，则m＞n
【分析】根据图象可得，该一次函数的图象过一、二、四象限，进而可得k、b的值与函数的增减性，即可判断A、C、D；直线y＝kx+b（k≠0）与x轴交点的横坐标的值是方程kx+b＝0的解，即可判断B．
解：∵一次函数y＝kx+b（k≠0）的图象过一、二、四象限，
∴k＜0，b＞0，
故A、C错误，不符合题意；
∵直线y＝kx+b（k≠0）与x轴的交点为（1，0），
∴方程kx+b＝0的解是x＝1，
故B错误，不符合题意；
∵k＜0，
∴y随x的增大而减小，
∵3＞1，
∴m＞n
故D正确，符合题意．
故选：D．
【点评】本题考查了一次函数与一元一次方程的关系：一次函数y＝kx+b与x轴交点的横坐标的值是方程kx+b＝0的解．也一次函数的图象与系数的关系，以及一次函数的性质．
12．如图（1），在矩形ABCD中，动点P从点C出发，沿路线C→D→A做匀速运动，图（2）是此运动过程中，△PBC的面积S与点P运动的路程x之间的函数图象的一部分，则BC+CD的长为（　　）

A．5 B．6 C．7 D．12
【分析】由图象2看出当点P到达点C时，即x＝3时，△BPC的面积最大，根据面积公式求出BC的长即可．
解：由图（2）知，当x＝3时，点P由点C到达点D，
∴CD＝3，
∴BC•CD＝6，
∴BC＝4，
∴BC+CD＝4＝3＝7，
故选：C．
【点评】本题主要考查了动点问题的函数图象．解题的关键是利用函数的图象读懂当即x＝3时，△PBC的面积为6．
二、填空题（本大题6小题，每小題3分，满分18分；请将答案直接写在题中的横线上）
13．若函数y＝x+k﹣2为正比例函数，则k的值为 　2　．
【分析】根据正比例函数的定义：y＝kx（k为常数且k≠0），判断即可．
解：∵函数y＝x+k﹣2是正比例函数，
∴k﹣2＝0，
∴k＝2，
故答案为：2．
【点评】本题考查了正比例函数的定义，熟练掌握正比例函数的定义是解题的关键．
14．某工程队正在对一湿地公园进行绿化，中间休息了一段时间，已知绿化面积S（m2）与工作时间t（h）的函数关系的图象如图所示，则休息后工程队每小时绿化面积为 　50　m2．

【分析】根据图象可得，休息后园林队2小时绿化面积为170﹣70＝100（m2），然后可得绿化速度．
解：根据图象可得，休息后园林队2小时绿化面积为170﹣70＝100（m2）．
每小时绿化面积为100÷2＝50（m2）．
故答案为：50．
【点评】此题主要考查了函数图象，关键是正确理解题意，从图象中找出正确信息．
15．如图，△ABC向右平移4个单位得到△A1B1C1，则点A1的坐标是 　（1，2）　．

【分析】直接利用平移中点的变化规律求解即可．
解：将△ABC向右平移4个单位，得到△A1B1C1，点A、B、C的对应点分别为A1、B1、C1，
∵A（﹣3，2），
∴点A1的坐标为（﹣3+4，2），即（1，2）．
故答案为：（1，2）．
【点评】本题考查了坐标系中点、图形的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
16．如图，把直线y＝﹣2x向上平移后得到直线AB，直线AB经过点A（0，1），则直线AB的解析式是 　y＝﹣2x+1　．

【分析】根据平移后k值不变，可设直线AB的解析式是y＝﹣2x+b，再由直线AB经过点A（0，1），可得出b＝1，继而得出AB的解析式．
解：设直线AB的解析式为y＝﹣2x+b，
将点A（0，1）代入得：b＝1，
∴AB的解析式为：y＝﹣2x+1．
【点评】本题考查一次函数图象的几何变换，属于基础题，关键在于掌握平移k值不变的知识点及待定系数法的应用．
17．若点（m+1，2n﹣m）在x轴上，且到原点的距离为1，那么mn的值为 　0或﹣2　．
【分析】根据题意得，2n﹣m＝0且|m+1|＝0，求出m和n的值即可得到答案．
解：由题意得，，
解得，或，
∴mn＝0或2．
故答案为：0或﹣2．
【点评】本题考查了平面直角坐标系中点的坐标特征，解题的关键是求出m和n的值．
18．如图，在△ABC中，AB＝2022，AC＝2019，AD为中线，则△ABD与△ACD的周长之差＝　3　．

【分析】根据三角形的周长的计算方法得到△ABD的周长和△ADC的周长的差就是AB与AC的差．
解：∵AD是△ABC中BC边上的中线，
∴BD＝DC＝BC，
∴△ABD与△ACD的周长之差
＝（AB+BD+AD）﹣（AC+DC+AD）
＝AB﹣AC
＝2022﹣2019
＝3．
则△ABD与△ACD的周长之差＝3．
故答案为3．
【点评】本题考查三角形的中线的定义：三角形一边的中点与此边所对顶点的连线叫做三角形的中线，同时考查了三角形周长的计算方法．
三、解答题（本大题共8小题，满分66分；解答题应写出演算步骤或证明过程）
19．已知每千克化工原料的售价为120元，若x（元）表示购买m千克化工原料的总价钱．
（1）写出m与x的函数关系式；
（2）说出其中的变量与常量．
【分析】（1）根据单价、购买的总重量和总钱数的关系列关系式即可；
（2）根据变量和常量的定义：在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量可直接得到答案．
解：（1）由题意得：120m＝x，
∴．
（2）变量：m，x，常量：120．
【点评】本题考查了函数关系式的求法与常量和变量的定义，常量就是在变化过程中不变的量，变量就是可以取到不同数值的量．
20．已知点P（x，y）满足3x﹣2y＝2，求P（2m+4，m﹣1）的坐标．
【分析】根据题意可得3（2m+4）﹣2（m﹣1）＝2，然后进行计算即可解答．
解：由题意得：
3（2m+4）﹣2（m﹣1）＝2，
解得：m＝﹣3，
当m＝﹣3时，2m+4＝﹣2，
m﹣1＝﹣4，
∴P的坐标为（﹣2，﹣4）．
【点评】本题考查了点的坐标，准确熟练地进行计算是解题的关键．
21．在平面直角坐标系中，点P的坐标为（a﹣7，3﹣2a），将点P向上平移4个单位，再向右平移5个单位后得到点Q．
（1）若点Q位于第一象限，求a的取值范围．
（2）在（1）的条件下，若a为整数，求出P、Q两点坐标．
【分析】（1）依据点P向上平移4个单位，再向右平移5个单位后得到点Q（a﹣2，7﹣2a），点Q位于第一象限，即可得出a的取值范围．
（2）依据a为整数，2＜a＜3.5，即可得到a＝3，进而得出P、Q两点坐标．
解：（1）∵点P的坐标为（a﹣7，3﹣2a），
∴将点P向上平移4个单位，再向右平移5个单位后得到点Q（a﹣2，7﹣2a），
∵点Q位于第一象限，
∴，
解得2＜a＜3.5．
（2）∵a为整数且2＜a＜3.5，
∴a＝3，
∴P（﹣4，﹣3），Q（1，1）．
【点评】本题考查了坐标与图形变化﹣平移，平移中点的变化规律是：左右移动改变点的横坐标，左减，右加；上下移动改变点的纵坐标，下减，上加．
22．如图，函数y＝2x和y＝ax+4的图象相交于点A（m，3）．
（1）求m，a的值；
（2）根据图象，直接写出不等式2x＞ax+4的解集．

【分析】（1）首先把A（m，3）代入y＝2x，求得m的值，然后利用待定系数法求出a的值，
（2）以交点为分界，结合图象写出不等式2x＞ax+4的解集即可．
解：（1）把（m，3）代入y＝2x得，2m＝3，
解得，
∴点A的坐标为（，3），
∵函数y＝ax+4的图象经过点A，
∴，
解得；
（2）由图象得，不等式2x＞ax+4的解集为．
【点评】此题主要考查了一次函数与一元一次不等式，关键是求出A点坐标．
23．如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，AB＝13cm，BC＝12cm，AC＝5cm．
（1）求△ABC的面积；
（2）求CD的长．

【分析】（1）利用三角形的面积列式计算即可得解；
（2）根据三角形的面积列出方程求解即可．
解：（1）△ABC的面积＝AC•BC＝×5×12＝30cm2；

（2）∵CD是AB边上的高，
∴△ABC的面积＝AB•CD＝30，
即×13•CD＝30，
解得CD＝．
【点评】本题考查了三角形的面积，主要是直角三角形的面积的求法，是基础题．
24．Ⅰ号无人机从海拔10m处出发，以10m/min的速度匀速上升，Ⅱ号无人机从海拔30m处同时出发，以a（m/min）的速度匀速上升，经过tmin两架无人机位于同一海拔高度60m．无人机海拔高度y（m）与时间x（min）的关系如图．两架无人机都上升了20min．
（1）求t的值及Ⅱ号无人机海拔高度y（m）与时间x（min）的关系式；
（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高40米．

【分析】（1）由题意得：t＝＝5；再用待定系数法求出函数表达式即可；
（2）由题意得：（10x+10）﹣（6x+30）＝40，即可求解．
解：（1）由题意得：t＝＝5，
设函数的表达式为y＝kx+b，
将（0，30）、（5，60）代入上式得，
解得，
故函数表达式为y＝6x+30（0≤x≤20）；
（2）由题意得：（10x+10）﹣（6x+30）＝40，
解得x＝15＜20，
故无人机上升15min，Ⅰ号无人机比Ⅱ号无人机高40米．
【点评】本题考查的是一次函数的应用，根据题意确定y和x的表达式是本题解题的关键．
25．已知一次函数y＝kx+b（k≠0）的图象经过点（3，5）与（﹣4，﹣9）．
（1）求这个一次函数的解析式；
（2）判断点是否在这个一次函数的图象上；
（3）直接写出关于x的一元一次方程kx+b＝0的解．
【分析】（1）待定系数法求解析式即可；
（2）将代入一次函数解析式求出y的值，即可判断；
（3）由（2）可知一次函数过点（，0），即可求出方程kx+b＝0的解．
解：（1）∵一次函数y＝kx+b（k≠0）的图象经过点（3，5）与（﹣4，﹣9），
可得，
解得，
∴这个一次函数的解析式为y＝2x﹣1；
（2）当时，，
∴点C（，0）在这个一次函数的图象上；
（3）由（2）可得一元一次方程kx+b＝0的解．
【点评】本题考查了一次函数与一元一次方程，待定系数法求解析式，熟练掌握一次函数图象上点的坐标特征是解题的关键．
26．为了抓住中秋商机，某商店计划购进A，B两种月饼，若购进A种月饼10盒，B种月饼5盒，需要600元；若购进A种月饼5盒，B种月饼3盒，需要330元．
（1）求购进A、B两种月饼每盒需要多少元？
（2）若该商店决定拿出2400元全部用来购进两种月饼，考虑市场需求，要求购进A种月饼的数量不少于B种月饼数量6倍，且不超过B种月饼数量的8倍．请你分别求出该商店共有几种进货方案？
【分析】（1）关系式为：A的单价×数量+B的单价×数量＝总费用；
（2）关系式为：A需要的钱数+B需要的钱数＝6000；购进A种纪念品的数量不少于B种纪念品数量的6倍，且不超过B种纪念品数量的8倍．
解：（1）购进A，B两种月饼每盒分别是x元，y元．
，
解得：．
答：购进A，B两种月饼每盒分别是30元，60元；
（2）设购买A种月饼为a盒，B种月饼为b盒．则
，
解得 8≤b≤10．
则b＝8，9，10；
则a对应为 64，62；60．
答：商店共有3种进货方案．
【点评】本题考查了一元一次不等式组、二元一次不等式组的应用．解决本题的关键是读懂题意，找到符合题意的相应的关系式是解决问题的关键，注意第二问应求得整数解．