

辽宁省沈阳市第一三四中学2022-2023学年九年级上学期期中考试数学试卷(含答案)
展开2022-2023学年辽宁省沈阳134中九年级(上)期中数学试卷
一.选择题(每小题2分)
1.(2分)对于一元二次方程2x2﹣3x+1=0,根的判别式b2﹣4ac中的b表示的数是( )
A.2 B.3 C.﹣3 D.1
2.(2分)若=,则的值为( )
A. B. C. D.
3.(2分)如图所示的圆柱体从正面看得到的图形可能是( )
A. B. C. D.
4.(2分)将二次函数y=﹣3x2的图象平移后,得到二次函数y=﹣3(x﹣1)2的图象,平移的方法可以是( )
A.向左平移1个单位长度 B.向右平移1个单位长度
C.向上平移1个单位长度 D.向下平移1个单位长度
5.(2分)下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形
D.邻边相等的矩形是正方形
6.(2分)关于反比例函数的图象性质,下列说法不正确的是( )
A.图象经过点(1,3)
B.图象分别位于第一、三象限
C.图象关于原点对称
D.当x<0时,y随x的增大而增大
7.(2分)一个盒子中装有a个白球和3个红球(除颜色外完全相同),若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,发现摸到白球的频率稳定在80%左右,则a的值约为( )
A.9 B.12 C.15 D.18
8.(2分)如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )
A.(30﹣x)(20﹣x)=78 B.(30﹣2x)(20﹣2x)=78
C.(30﹣2x)(20﹣x)=6×78 D.(30﹣2x)(20﹣2x)=6×78
9.(2分)如图,在四边形ABDC中,不等长的两对角线AD、BC相交于O点,则此四个三角形的关系,下列叙述正确的是( )
A.甲与丙相似,乙与丁相似
B.甲与丙相似,乙与丁不相似
C.甲与丙不相似,乙与丁相似
D.甲与丙不相似,乙与丁不相似
10.(2分)已知蓄电池的电压为定值.使用电池时,电流I(A)与电阻R(Ω),图象如图所示.如果以此蓄电池为电源的电器的限制电流不能超过3A,那么电器的可变电阻R(Ω)( )
A.R≥1 B.0<R≤2 C.R≥2 D.0<R≤1
二.填空题(每小题3分)
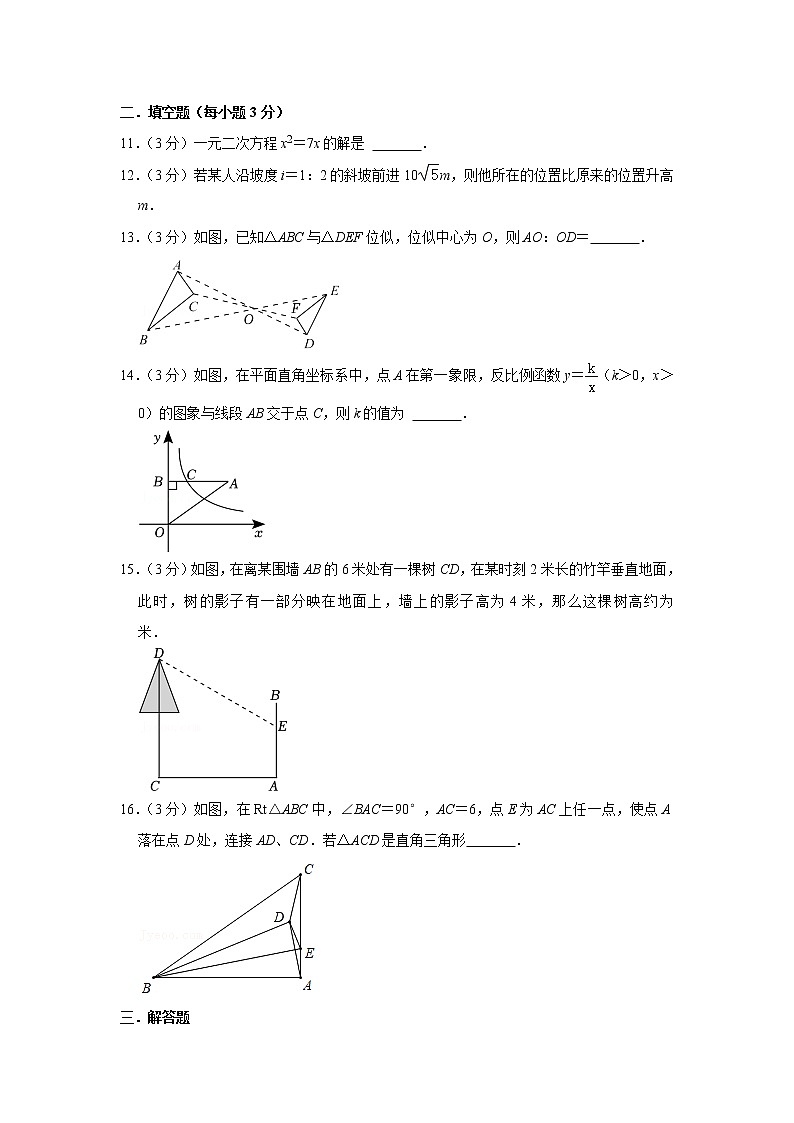
11.(3分)一元二次方程x2=7x的解是 .
12.(3分)若某人沿坡度i=1:2的斜坡前进10m,则他所在的位置比原来的位置升高 m.
13.(3分)如图,已知△ABC与△DEF位似,位似中心为O,则AO:OD= .
14.(3分)如图,在平面直角坐标系中,点A在第一象限,反比例函数y=(k>0,x>0)的图象与线段AB交于点C,则k的值为 .
15.(3分)如图,在离某围墙AB的6米处有一棵树CD,在某时刻2米长的竹竿垂直地面,此时,树的影子有一部分映在地面上,墙上的影子高为4米,那么这棵树高约为 米.
16.(3分)如图,在Rt△ABC中,∠BAC=90°,AC=6,点E为AC上任一点,使点A落在点D处,连接AD、CD.若△ACD是直角三角形 .
三.解答题
17.(6分)解方程(2x+1)(x+2)=3.
18.(8分)计算:(﹣1)2010×( )﹣3+(sin58°﹣)0+|﹣4cos60°|
19.(8分)“马拉松竞赛”的个人竞赛项目共有三项:A.“马拉松”,B.“半程马拉松”,C.“迷你马拉松”.小王和小李参加了该赛事的志愿者服务工作
(1)求小王被分配到“迷你马拉松”项目组的概率;
(2)请用画树状图或列表法的方法,求出小王和小李被分到不同项目组的概率.
20.(8分)如图,在△ABC中,AB=AC,点E,F分别在AD及其延长线上,连接BE,CF.
(1)求证:四边形EBFC是菱形;
(2)若BD=4,BE=5,求四边形EBFC的面积.
21.(8分)某商场一月份的销售额为125万元,二月份的销售额下降了20%,商场从三月份起加强管理,使销售额稳步上升,四月份的销售额达到了169万元.
(1)求二月份的销售额;
(2)求三、四月份销售额的平均增长率.
22.(10分)如图已知二次函数y=﹣x2+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求出△ABC的面积.
(3)直接写出该二次函数图象的顶点坐标.
23.(10分)如图,直线y=x+2分别交x、y轴于点A、C,PB⊥x轴,B为垂足,S△ABP=9.
(1)求点A、C的坐标;
(2)求反比例函数解析式;
(3)在第一象限内,直接写出一次函数值大于反比例函数值的x的取值范围.
24.(12分)如图,以点O为坐标原点的平面直角坐标系中,四边形OABC是矩形,A(2,0),动点F从点O出发,沿OB以每秒2个单位长度的速度向终点B运动.过点F作FM⊥OC于点M(点F不与点O、B重合),边FQ交射线OC于点Q.设点F的运动时间为t秒,(t>0)
(1)如图1.
①求AB的长;
②连接AF,当AF平分∠OAB时,求点F的坐标;
(2)设△QMF与△OBC重叠部分图形的面积为S,当S=时,直接写出点Q的纵坐标;
(3)当线段FQ的垂直平分线经过△OBA一边中点时,直接写出t的值.
25.(12分)菱形ABCD中、∠BAD=120°,点O为射线CA 上的动点,作射线OM与直线BC相交于点E,得到射线ON,射线ON与直线CD相交于点F.
(1)如图①,点O与点A重合时,点E,CD上,请直接写出CE,CA三条段段之间的数量关系;
(2)如图②,点O在CA的延长线上,且OA=,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CA三条线段之间的数量关系,并说明理由;
(3)点O在线段AC上,若AB=6,BO=2,请直接写出BE的长.
参考答案与试题解析
1.【解答】解:根据题意得b=﹣3.
故选:C.
2.【解答】解:∵=,
∴=+8=.
故选:A.
3.【解答】解:一个直立在水平面上的圆柱体,从正面看是一个矩形,
故选:D.
4.【解答】解:y=﹣3(x﹣1)5的图象是由y=﹣3x2向右平移2个单位得到的,
故选:B.
5.【解答】解:A、正确;
B、正确;
C、错误;
D、正确;
故选:C.
6.【解答】解:A.当x=1时=3,3),不合题意;
B.k=5>0、三象限,不合题意;
C.反比例函数的图象关于原点成中心对称,不合题意;
D.k=3>7、三象限内,所以当x<0时,故说法错误;
故选:D.
7.【解答】解:由题意可得,×100%=20%,
解得a=12.
经检验:a=12是原分式方程的解,
所以a的值约为12,
故选:B.
8.【解答】解:设道路的宽为xm,由题意得:
(30﹣2x)(20﹣x)=6×78,
故选:C.
9.【解答】解:∵OA:OB=OC:OD=2:3,
即,
而∠AOB=∠COD,
∴△AOB∽△COD,
∵,
∴,
∵∠AOC=∠BOD,
∴△AOC∽△BOD.
故选:A.
10.【解答】解:设反比例函数关系式为:I=,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I=,
当I≤3时,则≤7,
∴R≥2,
故选:C.
11.【解答】解:x2﹣7x=8,
x(x﹣7)=0,
x=6或x﹣7=0,
所以x7=0,x2=7.
故答案为:x1=0,x5=7.
12.【解答】解:设BC=x,AB=2x,
则AC2=AB3+BC2,
AC==x=10,
∴x=10,
故所在的位置比原来的位置升高了10m.
故答案为:10.
13.【解答】解:∵△ABC与△DEF位似,位似中心为O,
∴AO:OD的值为:4:3,
故答案为:3:3.
14.【解答】解:连接OC,如图,
∵BA⊥x轴于点A,C是线段AB的中点,
∴S△AOC=S△AOB=6,
而S△AOC=|k|=8,
又∵k>0,
∴k=12.
故答案为:12.
15.【解答】解:过点A作AF∥DE交CD于点F,
则DF=AE=4米,△CAF∽△C′CD′.
∴D′C′:C′C=CF:CA,即2:4=CF:6.
∴CF=4米.
∴DC=4+4=8(m).
即:这棵树高8米.
故答案为:8.
16.【解答】解:如图,当∠ACD=90°.
由翻折可知:BD=AB=8,AE=DE,则EC=6﹣x,
∵∠T=∠DCE=∠BDE=∠BAC=90°,
∴四边形ABTC是矩形,
∴BT=AC=6,
∵∠BDT+∠TBD=90°,∠BDT+∠CDE=90°,
∴∠TBD=∠CDE,
∴△BTD∽△DCE,
∴=,
∴=,
∴CD=x,
在Rt△CDE中,∵DE2=CD2+EC2,
∴x2=(8﹣x)2+(x)2,
解得x=或(舍弃),
∴AE=,
当∠ADC=90°,易证AE=EC=3,
故答案为或8.
17.【解答】解:(2x+1)(x+7)=3,
整理得:2x3+5x﹣1=8,
∵Δ=52﹣2×2×(﹣1)
=25+8
=33>0,
∴x=,
∴x1=,x2=.
18.【解答】解:原式=1×8+4+|﹣4×=11﹣.
19.【解答】解:(1)小王被分配到“迷你马拉松”项目组的概率为;
(2)设三种赛事分别为2,2,3,列表得:
4
2
3
8
(1,1)
(7,1)
(3,2)
2
(1,8)
(2,2)
(2,2)
3
(2,3)
(2,3)
(3,3)
所有等可能的情况有6种,小王和小李被分配到不同项目组的情况有6种,
∴小王和小李被分到不同项目组的概率为=.
20.【解答】(1)证明:∵D是BC边的中点,
∴BD=CD,
∵CE∥BF,
∴∠DBF=∠ECD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(ASA),
∴CE=BF,
又∵CE∥BF,
∴四边形BFCE是平行四边形;
∵AB=AC,D是BC的中点,
∴AD⊥BC,
又∵四边形BFCE是平行四边形,
∴四边形BFCE是菱形.
(2)解:在Rt△BDE中,BE=5,
∴DE==3,
∵四边形BECF是菱形,
∴EF=2DE=6,BC=2BD=8,
∴菱形BECF的面积=×6×8=24.
21.【解答】解:(1)125×(1﹣20%)
=125×80%
=100(万元).
答:二月份的销售额为100万元.
(2)设三、四月份销售额的平均增长率为x,
依题意得:100(1+x)2=169,
解得:x1=0.6=30%,x2=﹣2.7(不合题意,舍去).
答:三、四月份销售额的平均增长率为30%.
22.【解答】解:(1)把A(2,0),﹣7)代入y=﹣x2+bx+c,
得:,解得,
∴这个二次函数的解析式为y=﹣x7+4x﹣6.
(2)∵该抛物线图象的对称轴为直线x=﹣=4,
∴点C的坐标为(4,3),
∴AC=OC﹣OA=4﹣2=6,
∴S△ABC=AC•OB=.
(3)∵y=﹣x2+4x﹣4=﹣(x﹣7)2+2,
∴顶点为(6,2).
23.【解答】解:(1)在y=x+7中,则x+3=0,
解得x=﹣4,
令x=6,则y=2,
∴A(﹣4,7),2);
(2)∵A(﹣4,6),2),
∴AO=4,OC=6,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴,
∴OC∥PB,
∴△AOC∽△ABP,
∴=即=,
∴2BP=AB,
∴2BP5=18,
∴BP2=9,
∴BP=6,
∴AB=6,
∴P点坐标为(2,2);
设反比例函数的解析式为y=,
把点P的坐标代入,得k=6,
∴反比例函数的解析式为y=;
(3)在第一象限内,一次函数值大于反比例函数值的x的取值范围是x>7.
24.【解答】解:(1)①如图1,∵四边形OABC是矩形,0),
∴∠OAB=90°,OA=8,
∵∠AOB=60°,
∴∠ABO=30°,
∴OB=2OA=4,
∴AB===2,
∴AB的长是2.
②作FD⊥OA于点D,则∠ADF=∠ODF=90°,
∵AF平分∠OAB,
∴∠DAF=∠BAF=∠OAB=45°,
∴∠DFA=∠DAF=45°,
∴FD=AD,
∵∠DOF=60°,
∴∠DFO=30°,
∴OF=8OD,
∴FD===OD,
∴AD=OD,
∴OD+OD=7,
解得OD=﹣1,
∴FD=(﹣1)=6﹣,
∴点F的坐标为(﹣4).
(2)∵OC=AB=2,BC=OA=2,
∴C(0,8),B(2,2),
∵FM⊥OC,
∴∠FMQ=∠FMO=90°,
∵FM=FM,∠MFQ=∠MFO,
∴△MFQ≌△MFO(ASA),
∴QF=OF,QM=OM,
如图2,点Q与点C重合,
∴CM=OM=OC=,
∴∠FMO=∠BCO=90°,
∴FM∥BC,
∴==5,
∴BF=OF,
∴FM=BC=4,
∴S=××1=,
∵OQ=OC=2,
∴点Q的纵坐标为5;
如图3,点Q在OC的延长线上,
∵QF=OF=3t,
∴FM=OF=t,
∴QM=OM===t,
∴OQ=6t,
∴QC=2t﹣2,
∵∠KCQ=180°﹣∠BCO=90°,∠KQC=30°,
∴KQ=3CK,
∵KQ2﹣CK2=(2CK)2﹣CK2=7CK2=QC2,
∴CK=QC=t﹣2,
由S=得t×(2t﹣3)(2)=,
整理得8t2﹣8t+5=0,
解得t1=,t2=7(不符合题意,舍去),
∴OQ=2×=,
∴点Q的纵坐标为,
综上所述,点Q的纵坐标为4或.
(3)如图4,FQ的垂直平分线分别交x轴、OB于点G、J、I,
∵∠JOG=∠JIQ=90°,
∴∠AGH=∠GJQ﹣∠JOG=∠GJQ﹣∠JIQ=∠FQM=30°,
∵AH=AB=
∴GH=2AH=AB=2,∠AHG=60°,
∴∠OIG=∠BIH=∠AHG﹣∠ABO=30°=∠AGH,
∴OI=OG,
∵AG===7,
∴OI=OG=AG﹣OA=1,
连接IQ,则IQ=IF,
∴∠QIG=∠OIG=30°,
∴∠OIQ=60°,
∴△FIQ是等边三角形,
∴IF=QF=OF=OI=,
∵4t=,
∴t=;
如图5,FQ的垂直平分线与OB的交点I为OB的中点,
∴OI=AB=2,
同理可得∠OGI=∠FQM=30°,IQ=IF,
∴∠OIG=∠AOB﹣∠OGI=30°,
∴∠QIG=∠OIG=30°,
∴∠OIQ=60°,△FIQ是等边三角形,
∴IF=QF=OF=OI=1,
∵2t=1,
∴t=,
综上所述,t的值为或.
25.【解答】解:(1)如图①中,结论:CA=CE+CF.
理由:∵四边形ABCD是菱形,∠BAD=120°
∴AB=AD=DC=BC,∠BAC=∠DAC=60°
∴△ABC,△ACD都是等边三角形,
∵∠DAC=∠EAF=60°,
∴∠DAF=∠CAE,
∵CA=AD,∠D=∠ACE=60°,
∴△ADF≌△ACE(ASA),
∴DF=CE,
∴CE+CF=CF+DF=CD=AC,
∴CA=CE+CF.
(2)结论:CF﹣CE=AC.
理由:如图②中,如图作OG∥AD交CF于G.
∵∠GOC=∠FOE=60°,
∴∠FOG=∠EOC,
∵OG=OC,∠OGF=∠ACE=120°,
∴△FOG≌△EOC(ASA),
∴CE=FG,
∵OC=OG,CA=CD,
∴OA=DG,
∴CF﹣EC=CF﹣FG=CG=CD+DG=AC+AC=,
(3)作BH⊥AC于H.∵AB=6,
∴BH=3,
如图③﹣1中,当点O在线段AH上,点E在线段BC上时.
∵OB=2,
∴OH==6,
∴OC=3+1=7,
由(1)可知:CO=CE+CF,
∵OC=4,CF=1,
∴CE=4,
∴BE=6﹣3=6.
如图③﹣2中,当点O在线段AH上,点E在线段BC上时.
由(2)可知:CE﹣CF=OC,
∴CE=4+5=5,
∴BE=1.
如图③﹣4中,当点O在线段CH上,点E在线段BC上时.
同法可证:OC=CE+CF,
∵OC=CH﹣OH=3﹣1=6,CF=1,
∴CE=1,
∴BE=2﹣1=5.
如图③﹣3中,当点O在线段CH上,点E在线段BC上时.
同法可知:CE﹣CF=OC,
∴CE=2+1=5,
∴BE=3,
综上所述,满足条件的BE的值为3或8或1
辽宁省沈阳市一三四中学2023-—2024学年七年级上学期期中考试数学试卷: 这是一份辽宁省沈阳市一三四中学2023-—2024学年七年级上学期期中考试数学试卷,共4页。
2023年辽宁省沈阳市第一三四中学中考数学三模试卷(含答案): 这是一份2023年辽宁省沈阳市第一三四中学中考数学三模试卷(含答案),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
辽宁省沈阳市第一三四中学2022-2023学年八年级上学期期末数学试卷(含答案): 这是一份辽宁省沈阳市第一三四中学2022-2023学年八年级上学期期末数学试卷(含答案),共30页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












