

山东省日照市五莲县2022-2023学年八年级上学期期中考试数学试题(含答案)
展开2022-2023学年山东省日照市五莲县八年级第一学期期中数学试卷
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个是正请的,请将正确选项代号填入答题卡中)
1.自新冠肺炎疫情发生以来,全国人民共同抗疫,博才实验中学积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )
A.有症状早就医 B.防控疫情我们在一起
C.打喷嚏捂口鼻 D.勤洗手勤通风
2.一副三角板如图叠放在一起,则图中∠α的度数为( )
A.35° B.30° C.25° D.15°
3.已知等腰三角形的两边长分别为4cm、8cm,则该等腰三角形的周长是( )
A.12cm B.16cm C.16cm或20cm D.20cm
4.下列说法正确的是( )
A.三角形三条高交于三角形内一点
B.一个钝角三角形一定不是等腰三角形,也不是等边三角形
C.有两条边及其中一条边的对角对应相等的两个三角形全等
D.平面上两个全等的图形不一定关于某直线对称
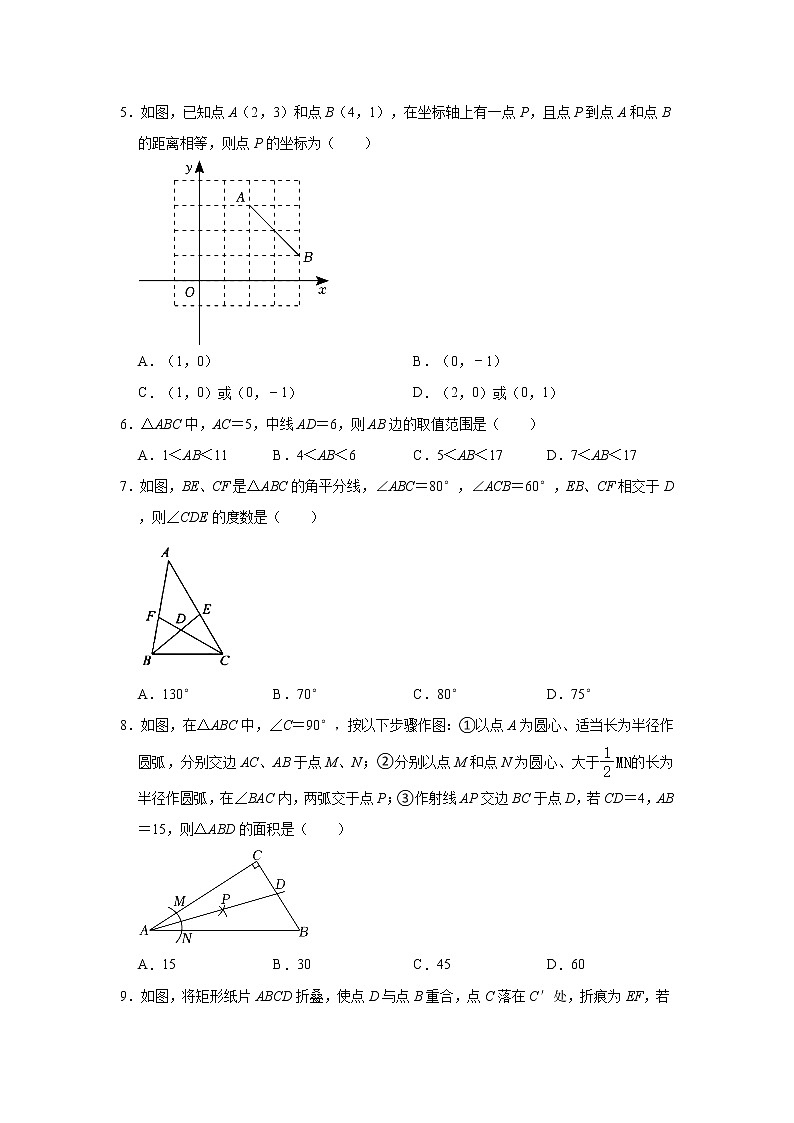
5.如图,已知点A(2,3)和点B(4,1),在坐标轴上有一点P,且点P到点A和点B的距离相等,则点P的坐标为( )
A.(1,0) B.(0,﹣1)
C.(1,0)或(0,﹣1) D.(2,0)或(0,1)
6.△ABC中,AC=5,中线AD=6,则AB边的取值范围是( )
A.1<AB<11 B.4<AB<6 C.5<AB<17 D.7<AB<17
7.如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,EB、CF相交于D,则∠CDE的度数是( )
A.130° B.70° C.80° D.75°
8.如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC、AB于点M、N;②分别以点M和点N为圆心、大于的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
9.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A.3 B.4 C.6 D.8
10.如图,△ABC是等边三角形,D为BA的中点,DE⊥AC,垂足为点E,EF∥AB,AE=1,下列结论错误的是( )
A.∠ADE=30° B.AD=2
C.△ABC的周长为10 D.△EFC的周长为9
11.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( )
A.15° B.22.5° C.30° D.45°
12.如图,已知△ABC和△CDE都是等边三角形,且A、C、E三点共线.AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
①AD=BE;②∠AOB=60°;③AP=BQ; ④△PCQ是等边三角形;⑤PQ∥AE.其中正确结论的有( )个.
A.5 B.4 C.3 D.2
二、填空题(本大题共4个小题;每小题4分,共16分,请把答案写在答题卡中的横线上)
13.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 ;其中边数最少的原多边形从一顶点出发,能作 条对角线.
14.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为 .
15.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为 .
16.△ABC在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(3,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 .
三、解答题(本大题共7小题,共68分.请把解答过程写在答题卡上,写在框外不得分.解答应写出文字说明、证明过程或演算步骤)
17.作图题:(不写作法,但必须保留作图痕迹)
如图:某地有两所大学和两条相交叉的公路,(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案.
18.如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=113°,求∠BCF的度数.
19.如图,已知AD∥BC一点E为CD上一点,AE、BE分别平分∠DAB、∠CBA,BE交AD的延长线于点F.
(1)求证:△ABE≌△AFE;
(2)求证:AD+BC=AB.
20.如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点△A1,B1,C1的坐标(直接写答案):A1 ;B1 ;C1 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.
21.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
22.已知如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC,交DE的延长线于点F,连接CF交AD于点G.试猜想AD和CF有什么关系?并证明你的猜想.
23.在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以acm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
(3)若∠C=70°,当∠CPQ的度数为多少时,△CPQ为等腰三角形?(请直接写出答案,不必写出过程).
参考答案
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个是正请的,请将正确选项代号填入答题卡中)
1.自新冠肺炎疫情发生以来,全国人民共同抗疫,博才实验中学积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )
A.有症状早就医 B.防控疫情我们在一起
C.打喷嚏捂口鼻 D.勤洗手勤通风
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形进行分析即可.
解:A、不是轴对称图形,不合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不合题意;
D、不是轴对称图形,不合题意.
故选:B.
【点评】此题主要考查了轴对称图形,正确掌握轴对称图形的定义是解题关键.轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合.
2.一副三角板如图叠放在一起,则图中∠α的度数为( )
A.35° B.30° C.25° D.15°
【分析】根据三角形的外角的性质列式计算即可.
解:∠α=60°﹣45°
=15°,
故选:D.
【点评】本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
3.已知等腰三角形的两边长分别为4cm、8cm,则该等腰三角形的周长是( )
A.12cm B.16cm C.16cm或20cm D.20cm
【分析】题中没有指明哪个是底哪个是腰,所以应该分两种情况进行分析.
解:当腰长为4cm时,4+4=8cm,不符合三角形三边关系,故舍去;
当腰长为8cm时,符合三边关系,其周长为8+8+4=20cm.
故该三角形的周长为20cm.
故选:D.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
4.下列说法正确的是( )
A.三角形三条高交于三角形内一点
B.一个钝角三角形一定不是等腰三角形,也不是等边三角形
C.有两条边及其中一条边的对角对应相等的两个三角形全等
D.平面上两个全等的图形不一定关于某直线对称
【分析】选项A根据三角形的高的定义判断即可;选项B根据等腰三角形的定义判断即可;选项C根据全等三角形的判定方法判断即可;选项D根据轴对称的性质判断即可.
解:A.锐角三角形的三条高交于三角形内一点,直角三角形的三条高相交于直角三角形的直角的顶点上,钝角三角形的三条高相交在钝角三角形的外部,故原题说法错误,故本选项不合题意;
B.一个钝角三角形不一定不是等腰三角形,故原题说法错误,故本选项不合题意;
C.有两条边及其中一条边的对角对应相等的两个三角形不一定全等,故原题说法错误,故本选项不合题意;
D.平面上两个全等的图形不一定关于某直线对称,说法正确,故本选项符合题意.
故选:D.
【点评】本题考查了轴对称的性质,全等三角形的判定方法以及三角形的高,掌握相关定义是解答本题的关键.
5.如图,已知点A(2,3)和点B(4,1),在坐标轴上有一点P,且点P到点A和点B的距离相等,则点P的坐标为( )
A.(1,0) B.(0,﹣1)
C.(1,0)或(0,﹣1) D.(2,0)或(0,1)
【分析】连接CP'交x轴于点P,点P与点P'即为所求的点,根据点的位置写出坐标即可得出选项.
解:如图,连接CP'交x轴于点P,
∵AP'=,
AP==BP,
∴点P与点P'即为所求的点,
即P(1,0)或P'(0,﹣1),
故选:C.
【点评】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
6.△ABC中,AC=5,中线AD=6,则AB边的取值范围是( )
A.1<AB<11 B.4<AB<6 C.5<AB<17 D.7<AB<17
【分析】延长AD到E使DE=AD,连接CE,通过SAS证明△ABD≌△ECD得出AB=EC,再根据三角形三边关系即可推出结果.
解:如图,延长AD到E使DE=AD,连接CE,
在△ABD与△ECD中,
,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵AE=AD=12,AC=5,
根据三角形三边关系得:12﹣5<EC<12+5,
即7<AB<17,
故选:D.
【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
7.如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,EB、CF相交于D,则∠CDE的度数是( )
A.130° B.70° C.80° D.75°
【分析】由BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,根据角平分线的定义,可求得∠EBC与∠FCB的度数,然后又三角形外角的性质,求得∠CDE的度数.
解:∵BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,
∴∠CBE=∠ABC=40°,∠FCB=∠ACB=30°,
∴∠CDE=∠CBE+∠FCB=70°.
故选:B.
【点评】此题考查了三角形内角和定理、三角形外角的性质以及角平分线的定义,注意掌握数形结合思想的应用.
8.如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC、AB于点M、N;②分别以点M和点N为圆心、大于的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
解:作DE⊥AB于E,
由基本作图可知,AP平分∠CAB
∵AP平分∠CAB,∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=30,
故选:B.
【点评】本题考查基本作图、角平分线的性质定理、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题.
9.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
A.3 B.4 C.6 D.8
【分析】由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.
解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,
∵∠ABE+∠EBF=∠C′BF+∠EBF=90°
∴∠ABE=∠C′BF
在△BAE和△BC′F中,
,
∴△BAE≌△BC′F(ASA),
∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,
△ABE和△BC′F的周长=2△ABE的周长=2×3=6.
故选:C.
【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,折叠前后图形的形状和大小不变,如本题中折叠前后角边相等.
10.如图,△ABC是等边三角形,D为BA的中点,DE⊥AC,垂足为点E,EF∥AB,AE=1,下列结论错误的是( )
A.∠ADE=30° B.AD=2
C.△ABC的周长为10 D.△EFC的周长为9
【分析】解直角三角形求出AD=2即可解决问题.
解:∵△ABC是等边三角形,
∴∠A=60°,AB=BC=AC,
∵DE⊥AC,
∴∠AED=90°,
∴∠ADE=30°
∵AE=1,
∴AD=2AE=2,故选项A,B正确,
∵AD=DB=2,
∴AB=BC=AC=4,
∴△ABC的周长为12,故选项C错误.
∵EF∥AB,
∴∠CEF=∠A=60°,∠EFC=∠B=60°,
∴△EFC是等边三角形,
∴△EFC的周长=3×(4﹣1)=9,故选项D正确,
故选:C.
【点评】本题考查等边三角形的判定和性质,解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
11.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( )
A.15° B.22.5° C.30° D.45°
【分析】过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可求出答案.
解:
过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°,
故选:C.
【点评】本题考查了轴对称﹣最短路线问题,等边三角形的性质,等腰三角形的性质,平行线分线段成比例定理等知识点的应用.
12.如图,已知△ABC和△CDE都是等边三角形,且A、C、E三点共线.AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
①AD=BE;②∠AOB=60°;③AP=BQ; ④△PCQ是等边三角形;⑤PQ∥AE.其中正确结论的有( )个.
A.5 B.4 C.3 D.2
【分析】结合等边三角形的性质、全等三角形的判定与性质依次对各个结论分析即可作出判断.
解:①∵△ABC和△CDE为等边三角形,
∴AC=BC,CD=CE,∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,①正确;
②∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵△DCE是等边三角形,
∴∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,②正确;
④∵∠DCP=60°=∠ECQ,
∴在△CDP和△CEQ中,
∠ADC=∠BEC,CD=CE,∠DCP=∠ECQ,
∴△CDP≌△CEQ(ASA).
∴CP=CQ,
∴∠CPQ=∠CQP=60°,△PCQ是等边三角形,④正确;
⑤∵∠CPQ=∠CQP=60°,
∴∠QPC=∠BCA,
∴PQ∥AE,⑤正确;
③同④得:△ACP≌△BCQ(ASA),
∴AP=BQ,③正确;
故选:A.
【点评】本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.
二、填空题(本大题共4个小题;每小题4分,共16分,请把答案写在答题卡中的横线上)
13.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 15或16或17 ;其中边数最少的原多边形从一顶点出发,能作 12 条对角线.
【分析】先求出新多边形的边数,再根据截去一个角后的多边形与原多边形的边数相等,多1,少1三种情况进行讨论;根据n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线解答即可.
解:设新多边形的边数为n,则(n﹣2)⋅180°=2520°,
解得n=16,
①若截去一个角后边数增加1,则原多边形边数为15;
②若截去一个角后边数不变,则原多边形边数为16;
③若截去一个角后边数减少1,则原多边形边数为17;
所以多边形的边数可以为15,16或17.
从十五边形的一顶点出发,能作的对角线的条数为:
n﹣3=15﹣3=12(条).
故答案为:15或16或17,12.
【点评】本题考查了多边形的内角和定理、多边形的对角线,解题的关键在于截去一个角后的多边形与原多边形的边数相等,多1,少1,有这么三种情况.
14.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为 12米 .
【分析】先判断出机器人所走过的路线是正多边形,然后用多边形的外角和除以每一个外角的度数求出多边形的边数,再根据周长公式列式进行计算即可得解.
解:根据题意得,机器人所走过的路线是正多边形,
∵每一次都是左转30°,
∴多边形的边数=360°÷30°=12,
周长=12×1=12米.
故答案为:12米.
【点评】本题考查了多边形的内角与外角,判断出走过的路线是正多边形是解题的关键.
15.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为 120° .
【分析】根据半角三角形的定义得出β的度数,再由三角形内角和定理求出另一个内角即可.
解:∵α=20°,
∴β=2α=40°,
∴最大内角的度数=180°﹣20°﹣40°=120°.
故答案为:120°.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
16.△ABC在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(3,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 (4,﹣1)或(﹣1,3)或(﹣1,﹣1). .
【分析】画出图形,即可直接解答.
解:如图:
故答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1).
【点评】本题考查的是全等三角形的判定,根据题意画出图形是解答此题的关键.
三、解答题(本大题共7小题,共68分.请把解答过程写在答题卡上,写在框外不得分.解答应写出文字说明、证明过程或演算步骤)
17.作图题:(不写作法,但必须保留作图痕迹)
如图:某地有两所大学和两条相交叉的公路,(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案.
【分析】先连接MN,根据线段垂直平分线的性质作出线段MN的垂直平分线DE,再作出∠AOB的平分线OF,DE与OF相交于P点,则点P即为所求.
解:如图所示:
(1)连接MN,分别以M、N为圆心,以大于MN为半径画圆,两圆相交于DE,连接DE,则DE即为线段MN的垂直平分线;
(2)以O为圆心,以任意长为半径画圆,分别交OA、OB于G、H,再分别以G、H为圆心,以大于GH为半径画圆,两圆相交于F,连接OF,则OF即为∠AOB的平分线(或∠AOB的外角平分线);
(3)DE与OF相交于点P,则点P即为所求.
【点评】本题考查的是线段的垂直平分线及角平分线的作法及性质,熟知此知识是解答此题的关键.
18.如图,在△ABC中,CD是AB边上高,BE为角平分线,若∠BFC=113°,求∠BCF的度数.
【分析】根据三角形的外角的性质求出∠ABE,根据角平分线的定义求出∠CBF,根据三角形内角和定理计算即可.
解:∵CD是AB边上高,
∴∠BDF=90°,
∠ABE=∠BFC﹣∠BDF=113°﹣90°=23°,
∵BE为角平分线,
∴∠CBF=∠ABE=23°,
∴∠BCF=180°﹣∠BFC﹣∠CBF=44°.
【点评】本题考查的是三角形内角和定理的应用、三角形的外角的性质,掌握三角形内角和等于180°是解题的关键.
19.如图,已知AD∥BC一点E为CD上一点,AE、BE分别平分∠DAB、∠CBA,BE交AD的延长线于点F.
(1)求证:△ABE≌△AFE;
(2)求证:AD+BC=AB.
【分析】(1)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据两直线平行,内错角相等可得∠2=∠F,然后求出∠1=∠F,再利用“角角边”证明△ABE和△AFE全等即可;
(2)根据全等三角形对应边相等可得BE=FE,然后利用“角边角”证明△BCE和△FDE全等,根据全等三角形对应边相等可得BC=DF,然后根据AD+BC整理即可得证.
【解答】(1)证明:如图,∵AE、BE分别平分∠DAB、∠CBA,
∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠2=∠F,∠1=∠F,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS);
(2)证明:∵△ABE≌△AFE,
∴BE=EF,
在△BCE和△FDE中,
,
∴△BCE≌△FDE(ASA),
∴BC=DF,
∴AD+BC=AD+DF=AF=AB,
即AD+BC=AB.
【点评】本题考查了全等三角形的判定与性质,平行线的性质,熟练掌握三角形全等的判定方法是解题的关键.
20.如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点△A1,B1,C1的坐标(直接写答案):A1 (3,2) ;B1 (4,﹣3) ;C1 (1,﹣1) ;
(3)△A1B1C1的面积为 6.5 ;
(4)在y轴上画出点P,使PB+PC最小.
【分析】(1)根据关于y轴对称点的性质得出各对应点位置进而得出答案;
(2)利用(1)中作画图形,进而得出各点坐标;
(3)利用△ABC所在矩形面积减去△ABC周围三角形面积进而求出即可;
(4)利用轴对称求最短路径的方法得出答案.
解:(1)如图所示:△A1B1C1,即为所求;
(2)A1(3,2);B1(4,﹣3);C1(1,﹣1);
故答案为:(3,2);(4,﹣3);(1,﹣1);
(3)△A1B1C1的面积为:3×5﹣×2×3﹣×1×5﹣×2×3=6.5;
(4)如图所示:P点即为所求.
【点评】此题主要考查了轴对称变换以及三角形面积求法等知识,正确利用轴对称图形的性质得出是解题关键.
21.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
【分析】(1)根据线段垂直平分线性质得出AD=BD,CE=AE,求出△ADE的周长=BC,即可得出答案;
(2)由∠BAC=130°,即可得∠B+∠C=50°,又由DA=DB,EA=EC,即可求得∠DAE的度数.
解:(1)在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6;
(2)∵∠BAC=130°,
∴∠B+∠C=50°,
∵DA=DB,EA=EC,
∴∠BAD=∠B,∠EAC=∠C,
∴∠BAD+∠EAC=50°,
∴∠DAE=∠BAC﹣(∠BAD+∠EAC)=130°﹣50°=80°.
【点评】本题考查了线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段的两个端点的距离相等.
22.已知如图,△ABC中,∠ACB=90°,AC=BC,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC,交DE的延长线于点F,连接CF交AD于点G.试猜想AD和CF有什么关系?并证明你的猜想.
【分析】先证出CD=DB,BF=DB,得出BF=CD,再证出∠CBF=∠ACD,由BC=AC,即可证出Rt△CBF≌Rt△ACD(SAS),得到AD=CF,∠BCF=∠CAD,从而证出∠AGC=90°,得出AD⊥CF.
解:AD=CF,AD⊥CF.
证明:∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵DE⊥AB,∴∠BDE=∠CBA=45°,
∵BF∥AC,∴∠DBF=180°﹣900=900,
∴△DBF为等腰直角三角形,BF=BD,
∵D为BC的中点,∴BF=BD=CD.
在△ACD和△CBF中
∴△ACD≌△CBF(SAS)
∴AD=CF,
∴∠CAD=∠BCF,
∵∠ACD=90°,即∠ACG+∠BCF=90°,
∴∠ACG+∠CAG=90°,∴∠AGC=90°,
∴AD⊥CF.
【点评】本题考查了等腰直角三角形的性质和全等三角形的判定与性质;证明三角形全等是关键.
23.在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以acm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
(3)若∠C=70°,当∠CPQ的度数为多少时,△CPQ为等腰三角形?(请直接写出答案,不必写出过程).
【分析】(1)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)分两种情况;①当∠BPD=90°时,由∠B=60°,得到∠BDP=30°,求得2BP=BD=10,求出x=2.5;②当∠BDP=90°时,根据三角形的内角和得到∠BPD=30°,求出x=10;即可得到当P出发2.5秒或10秒后,△BPD为直角三角形;
(3)分点P在边BC上或点P在边BC的延长线上,△CPQ为等腰三角形,根据等腰三角形的性质和三角形的内角和即可得到结论.
解:(1)∵AB=AC,
∴∠B=∠C,
∵AB=20cm,D是AB的中点,
∴BD=10cm,
∵点Q的速度与点P的速度不同,
∴BP≠CQ,
要使△BPD和△CQP全等,
则BP=CP=8cm CQ=BD=10cm,
∴x=秒,
∴a==cm/s;
(2)①当∠BPD=90°时,
∵∠B=60°,∴∠BDP=30°,
∴2BP=BD=10,
∴BP=5,
即2x=5,
∴x=2.5;
②当∠BDP=90°时,
∵∠B=60°,
∴∠BPD=30°,
∴BP=2BD=20,
即2x=20,
∴x=10
∴当P出发2.5秒或10秒后,△BPD为直角三角形;
(3)点P在边BC上,△CPQ为等腰三角形,
①当PQ=CQ,∵∠C=70°,
∴∠CPQ=∠C=70°,
②当PQ=PC,∵∠C=70°,
∴∠PQC=∠C=70°,
∴∠CPQ=180°﹣2×70°=40°,
③当PC=CQ,∵∠C=70°,
∴∠CPQ=∠CQP==55°,
点P在边BC的延长线上,△CPQ为等腰三角形,
∵∠ACB=70°,∴∠ACP=110°,
∵PC=CQ,
∴∠CPQ=∠CQP==35°,
综上所述:当△CPQ为等腰三角形时,∠CPQ的度数为35°,40°,55°,70°.
【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质和判定,三角形的内角和,直角三角形的性质,熟练掌握全等三角形的判定是解题的关键.
2022-2023学年山东省日照市五莲县八年级下学期期中数学试题及答案: 这是一份2022-2023学年山东省日照市五莲县八年级下学期期中数学试题及答案,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
山东省日照市五莲县2023-2024学年八年级上学期期末数学试题(含答案): 这是一份山东省日照市五莲县2023-2024学年八年级上学期期末数学试题(含答案),共10页。试卷主要包含了本试题分第Ⅰ卷和第Ⅱ卷两部分,在草稿纸、试卷上答题均无效,下列式子的变形正确的是,设是实数,定义一种新运算等内容,欢迎下载使用。
山东省日照市五莲县2022-2023学年七年级下学期6月期末数学试题: 这是一份山东省日照市五莲县2022-2023学年七年级下学期6月期末数学试题,共6页。












