初中数学北师大版八年级上册5 三角形的内角和定理获奖ppt课件

这是一份初中数学北师大版八年级上册5 三角形的内角和定理获奖ppt课件，共16页。PPT课件主要包含了教学目标，随堂练习，小组讨论，∠BDC27°，∠BFD118°，自主探索，课堂小结等内容，欢迎下载使用。

北师大版八年级《数学》上册
7.5.2三角形内角和定理
1.掌握三角形外角的两条性质；2.进一步熟悉和掌握证明的步骤、格式、方法、技巧．3.灵活运用三角形的外角和两条性质解决相关问题。4.进一步培养学生的逻辑思维能力和推理能力，培养学生的几何意识。5.通过在数学活动中进行教学，使学生能自主地“做数学”，特别是培养有条理的想象和探索能力，从而做到强化基础，激发学习兴趣．
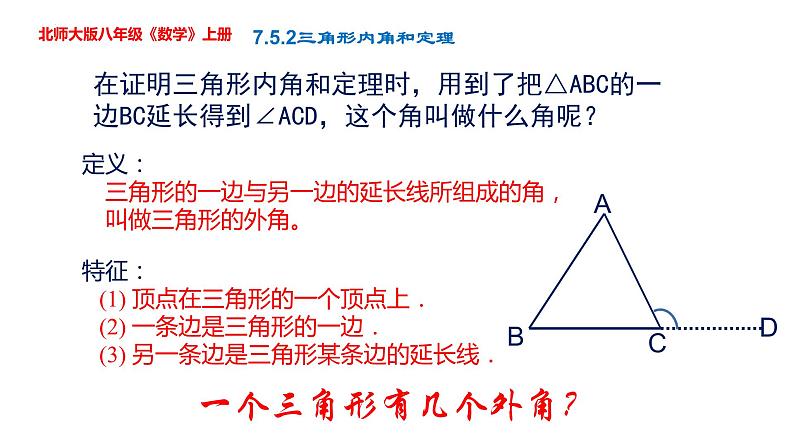
在证明三角形内角和定理时，用到了把△ABC的一边BC延长得到∠ACD，这个角叫做什么角呢？
定义： 三角形的一边与另一边的延长线所组成的角， 叫做三角形的外角。
特征： (1) 顶点在三角形的一个顶点上． (2) 一条边是三角形的一边． (3) 另一条边是三角形某条边的延长线．
一个三角形有几个外角？
7.5.2三角形内角和定理
证明：三角形的一个外角等于和它不相邻的两个内角的和．
证明：∵ ∠4 +∠2+ ∠3=180° （三角形内角和定理） 即∠2+ ∠3= 180°-∠4 又∵ ∠1+ ∠4= 180°(1平角= 180°) 即∠1 = 180°-∠4 ∴ ∠ 1= ∠2+ ∠3 (等量代换)
已知：如图，∠1是△ABC的一个外角.求证： ∠1= ∠2+ ∠3
证明：三角形的一个外角大于任何一个和它不相邻的内角．
已知：如图，∠1是△ABC的一个外角.求证： ∠1> ∠2, ∠1> ∠3
证明: ∵ ∠1 =∠2+ ∠3 （三角形的一个外角等于和它不相邻的两内角和） ∴ ∠1>∠2, ∠1>∠3
在这里,我们通过三角形的内角和定理直接推导出两个新定理．像这样，由一个基本事实或定理直接推出的定理，叫做这个基本事实或定理的推论( crllary )．推论可以当做定理使用.
定理 三角形的一个外角等于和它不相邻的两个内角的和.
定理 三角形的一个外角大于任何一个和它不相邻的内角.
例 已知:如图7—18，在△ABC中，∠B=∠C，AD平分外角∠EAC.求证:AD// BC.分析:要证明AD // BC，只需证明“同位角相等”或“内错角相等”或“同旁内角互补”.
证明:∵EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角的和)，∠B=∠C(已知)，∴∠C=∠EAC（等式的性质)∵AD平分∠EAC(已知)，∴∠DAC=∠EAC(角平分线的定义)∴∠DAC=∠C(等量代换).∴AD/ BC （内错角相等,两直线平行).
例 已知:如图，P是△ABC内一点，连接PB，PC求证:∠BPC>∠A.
证明:如图，延长BP，交AC于点D.∵∠BPC是△PDC的一个外角(外角的定义),∴∠BPC>∠PDC (三角形的一个外角大于任何一个和它不相邻的内角).∵∠PDC是△ABD的一个外角(外角的定义),∴∠PDC>∠A (三角形的一个外角大于任何一个和它不相邻的内角).∴∠BPC>∠A.
你还有其他的证明方法吗?与同伴进行交流.
1．如图，在△ABC中，∠A=45°，外角∠DCA=100°.求∠B和∠ACB的度数.
证明:∵∠DCA是△ABC的一个外角(已知),∴∠DCA=∠A+∠B (三角形的一个外角等于与它不相邻的两个内角之和).∵∠A=45°，∠DCA=100°(已知),∴∠ACB=∠DC-∠A=55°
证明：∵ ∠1 +∠BAF=180°(1平角= 180°) ∠2 +∠CBD=180° ∠3 +∠ACE=180°又∵ ∠1+ ∠2 + ∠3= 180° (三角形内角和定理)∴ ∠1+ ∠2 + ∠3 +∠BAF +∠CBD +∠ACE=3× 180°∴ ∠BAF +∠CBD +∠ACE=540 ° - 180°= 360°
2.已知：∠BAF，∠CBD，∠ACE是△ABC的三个外角． 求证：∠BAF+∠CBD+∠ACE=360°.
7.5.1三角形内角和定理
3.已知:如图，D是△ABC的边BC上的一点，∠DAC=∠B.求证：∠ADC=∠BAC.
证明：在△ABC和△ADC中，∠B +∠C+∠BAC=180°(三角形内角和定理)∠DAC +∠C+∠ADC=180°(同上） ∵ ∠DAC=∠B (已知）∴∠ADC=∠BAC
4.如图，求证:(1)∠BDC>∠A;(2)∠BDC=∠B+∠C+∠A.
证明：（1）连接AD并延长至E，如图。∠1=∠BAD+∠B（三角形外角定理）∠2=∠CAD+∠C∴∠1>∠BAD，∠2>∠CAD∴∠1+∠2>∠BAD+∠CAD（2）由（1）可知∠1=∠BAD+∠B。∠2=∠CAD+∠C（已证）∠1+∠2=∠BDC∴∠BDC=∠B+∠C+∠A
5.已知：D是直线AB上一点，E是直线AC上一点，直线BE与直线CD相交于F，∠BAC=62°,若 ∠ACD=35°,∠ABE=20°.求（1）∠BDC度数； （2）∠BFD度数．
6.已知：如图,在三角形ABC中,AD平分外角∠EAC,∠B=∠C.求证：AD∥BC
提示：利用外角定理和角平分线性质找角的相等关系
本节课学习了什么知识？
三角形的一个外角等于和它不相邻的两个内角的和
三角形的一个外角大于任何一个和它不相邻的内角