






数学必修 第一册1.1.1 集合及其表示方法图文ppt课件
展开1.1.1 集合及其表示方法
课前预习 课中探究 课堂评价
探究点一 列举法表示集合探究点二 用描述法表示集合探究点三 用区间表示集合探究点四 与方程解集有关的集合问题
能用符号语言刻画集合,能正确使用区间符号表示某些集合.
知识点一 集合的表示法
1.列举法:把集合中的元素 出来(相邻元素之间用逗号分隔),并写在大括号内,以此来表示集合的方法称为列举法. 2.描述法:一般地,如果属于集合A的任意一个元素x都具有性质p(x),而不属于集合A的元素都不具有这个性质,则性质p(x)称为集合A的一个特征性质.此时,集合A可以用它的特征性质p(x)表示为 ,这种表示集合的方法,称为特征性质描述法,简称为描述法. 集合{x|p(x)}中所有在另一个集合I中的元素组成的集合,可以表示为 .
【诊断分析】 判断正误.(请在括号中打“√”或“×”)(1)方程(x-1)(x+2)=0的实数根组成的集合为{-2,1}.( )(2)由直线y=2x+4上的横坐标和纵坐标都是自然数的点组成的集合为{x,y|y=2x+4,x∈N}.( )(3)集合{(1,2)}中的元素是1和2.( )
[解析] (1)正确.解方程得x=-2或x=1,用列举法表示其组成的集合为{-2,1}.
[解析] (2)直线上的点是点集,不是数集,因此用描述法表示为{(x,y)|y=2x+4,x∈N}.
[解析] (3)所给集合的元素是点集,所以元素应当为(1,2).
知识点二 区间及其表示
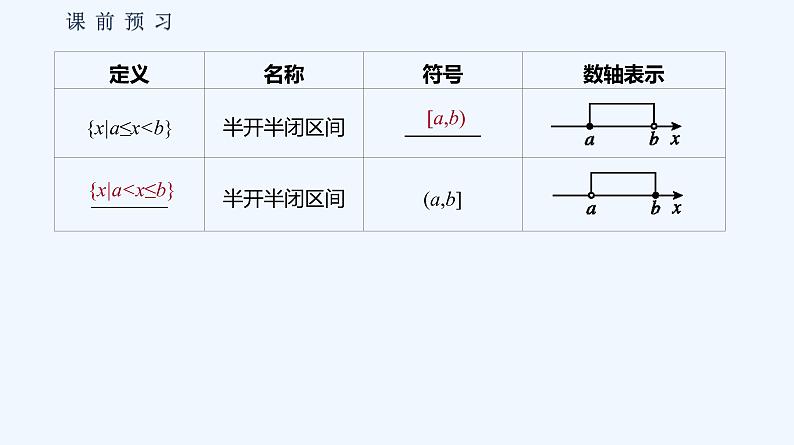
1.已知a,b是两个实数,且a
【诊断分析】 在集合{x|a≤x≤b}中,当a=b时,集合为{a},那么在区间[a,b]中,a,b是否可以相等?
解:无论是闭区间还是开区间,区间中的两个端点都不能相等,这是集合与区间的不同之处.
例1 用列举法表示下列集合,并指出是有限集还是无限集.(1)绝对值小于3的整数组成的集合; (2)方程(x-2)2+|y+1|=0的解组成的集合;(3)被3除余2的正整数组成的集合.
探究点一 列举法表示集合
变式 用列举法表示下列集合,并判断是有限集还是无限集.(1)从正方形ABCD的四个顶点中任取三个为顶点作三角形,由这些三角形组成的集合;(2)方程(x-2)2(x+1)=0的根组成的集合;(3)一次函数y=2x与y=x+2的图像的交点组成的集合.
[素养小结]列举法表示集合的步骤及注意事项:(1)列举法表示集合要分清元素的属性,元素与元素之间用“,”隔开.(2)列元素时要做到不重复、不遗漏.(3)元素个数较少的有限集或元素间存在明显规律的无限集可用列举法表示.但具有一定规律的无限集,如{1,2,3,4,…},就要考虑元素间的规律性,不能写成{2,1,4,3,…}.列举法在表示无限集时若用到字母,则需要在集合后注明字母范围.
例2 用描述法表示下列集合,并指出是有限集还是无限集.(1)所有三角形组成的集合;(2)满足不等式5x+2>3x-4的实数x组成的集合;(3)平面直角坐标系中第四象限内的点组成的集合.
探究点二 用描述法表示集合
解:(1)所求集合为{x|x是三角形}.该集合是无限集.(2)由不等式5x+2>3x-4,解得x>-3,则所求集合为{x|x>-3}.该集合是无限集.(3)设点P(x,y)在第四象限,则x>0,y<0,所以平面直角坐标系中第四象限内的点组成的集合是{(x,y)|x>0且y<0}.该集合是无限集.
[素养小结]描述法表示集合的步骤及注意事项:(1)确定集合中元素的特征.(2)给出其满足的性质.(3)根据描述法的形式写出其满足的集合.(4)用描述法表示集合时,要注意表示形式的规范,在通常情况下,集合中竖线左侧元素的所属范围为实数集时可以省略不写.例如,方程x2+2x=0的实数解组成的集合可表示为{x∈R|x2+2x=0},也可写成{x|x2+2x=0}.
例3 用区间表示下列集合:(1){x|x≥3};(2){x|-1
解:(1)[3,+∞). (2)(-1,2].(3)(-∞,5).
变式 (1)若[2a+1,3a-1]为一个确定区间,则实数a的取值范围为 .
[素养小结]解决区间问题应注意的五点:(1)区间的左端点a必须小于右端点b,有时我们将b-a称为区间长度.对于只有一个元素的集合,我们仍然用集合来表示,如当a=b时,用{a}表示.(2)注意开区间(a,b)与点(a,b)在具体情景中的区别.(3)用数轴来表示区间时,要特别注意实心点与空心点的区别.(4)对于一个不等式的所有解组成的集合,我们既可以用集合形式来表示,也可以用区间形式来表示.(5)要注意区间表示实数集的几条原则:数集是连续的、左小、右大、开或闭不能混淆、用“+∞”或“-∞”作为区间端点时要用开区间符号.
例4 [2021·牡丹江三中高一期中] 已知集合A={x∈R|ax2-3x+2=0},其中a为常数,且a∈R.(1)若A是空集,求实数a的取值范围;(2)若A中只有一个元素,求a的值;(3)若A中至多只有一个元素,求实数a的取值范围.
探究点四 与方程解集有关的集合问题
1. 集合{x|0≤x<2}可用区间表示为( )A.(0,2)B.(0,2]C.[0,2)D.[0,2]
[解析] 集合A为半开半闭区间,可表示为[0,2).
2. 集合{(x,y)|y=2x-1} 表示( )A.方程y=2x-1B.点(x,y)C.平面直角坐标系中所有点组成的集合D.函数y=2x-1的图像上所有点组成的集合
[解析] (x,y)表示坐标平面上的点,且点(x,y)在函数y=2x-1的图像上.故选D.
5. 下列说法正确的是 .(填序号) ①集合{x∈N|x(x2-4)=0}与集合{0,-2,2}表示同一集合;②方程(x-a)(x+a)=0的所有实数根组成的集合可记为{-a,a};③全体偶数组成的集合为{x|x=2k,x∈Z}; ④集合{(x,y)|y=x}表示一条过原点的直线.
[解析] 由x(x2-4)=0得x=0或x=±2,因此集合{x∈N|x(x2-4)=0}={0,2},与集合{0,-2,2}不是同一个集合,故①错误;当a=0时,方程(x-a)(x+a)=0的根为x=0,方程(x-a)(x+a)=0的所有实数根组成的集合为{0},不能表示为{-a,a},故②错误;全体偶数组成的集合为{x|x=2k,k∈Z},故③错误;集合{(x,y)|y=x}表示直线y=x上的所有点,即集合{(x,y)|y=x}表示一条过原点的直线,故④正确.故填④.
元素的分析法:集合离不开元素,分析元素是解决集合问题的核心,元素分析法就是抓住元素进行分析.
例1 (1)给出以下5组集合:①M={(-5,3)},N={-5,3};②M={1,-3},N={3,-1};③M=∅,N={0};④M={x|x2-3x+2=0},N={y|y2-3y+2=0}.其中是相等集合的有( ) A.1组B.2组C.3组D.4组
[解析] 对于①,M={(-5,3)}中有一个元素,是点(-5,3),N={-5,3}中有两个元素-5,3;对于②,M={1,-3},N={3,-1},集合M和集合N中的元素不同;对于③,M=∅,N={0},M是空集,N中有一个元素0;对于④,M={x|x2-3x+2=0},N={y|y2-3y+2=0},M和N中都有两个元素1,2,所以M=N.故选A.
(2)已知集合A={x|x2+px+q=x},B={x|(x-1)2+p(x-1)+q=x+3},当A={2}时,集合B=( )A.{1} B.{1,2}C.{2,5} D.{1,5}
[解析] 由A={x|x2+px+q=x}={2}知,22+2p+q=2,且Δ=(p-1)2-4q=0,解得p=-3,q=4,则(x-1)2+p(x-1)+q=x+3可化为(x-1)2-3(x-1)+4=x+3,即(x-1)(x-5)=0,解得x=1或x=5,所以集合B={1,5}.
高中数学人教B版 (2019)必修 第一册1.1.1 集合及其表示方法教课ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册1.1.1 集合及其表示方法教课ppt课件,共30页。PPT课件主要包含了学习目标,探究点一集合的概念等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第一册第一章 集合与常用逻辑用语1.1 集合1.1.1 集合及其表示方法图文ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册第一章 集合与常用逻辑用语1.1 集合1.1.1 集合及其表示方法图文ppt课件,文件包含111《集合及其表示方法》第2课时课件PPTpptx、111《集合及其表示方法》第2课时教案docx等2份课件配套教学资源,其中PPT共37页, 欢迎下载使用。
数学必修 第一册1.1.1 集合及其表示方法课前预习ppt课件: 这是一份数学必修 第一册1.1.1 集合及其表示方法课前预习ppt课件,文件包含111《集合及其表示方法》第1课时课件PPTpptx、111《集合及其表示方法》第1课时教案docx等2份课件配套教学资源,其中PPT共30页, 欢迎下载使用。













