

高中人教A版 (2019)7.3* 复数的三角表示教案
展开板书设计
教学研讨
虽然本节内容为选学内容,不作考试要求,但是若能掌握复数的三角函数式,对于解决一些复数的相关问题会有一定的帮助,所以对本节内容建议教师还是加以重视,尤其是对学习需求层次比较高的学生来说,学会本节内容还是很有必要的.教学时需要注意一些含有正弦或余弦的复数代数形式,将它们转化为三角形式时要利用诱导公式,如,有
;
;
.
遇到这样的情况,若适当拓展加以练习是否会更好?
教学环节
教学内容
师生互动
设计意图
复习引入
1.复数的代数形式:.
2.复数的几何意义.
3.复数的模.
4.角的概念,
教师使用多媒体展示问题。
学生思考回答.
教师适时小结,引入新课.
复习回顾,为新知识的学习做好准备工作.
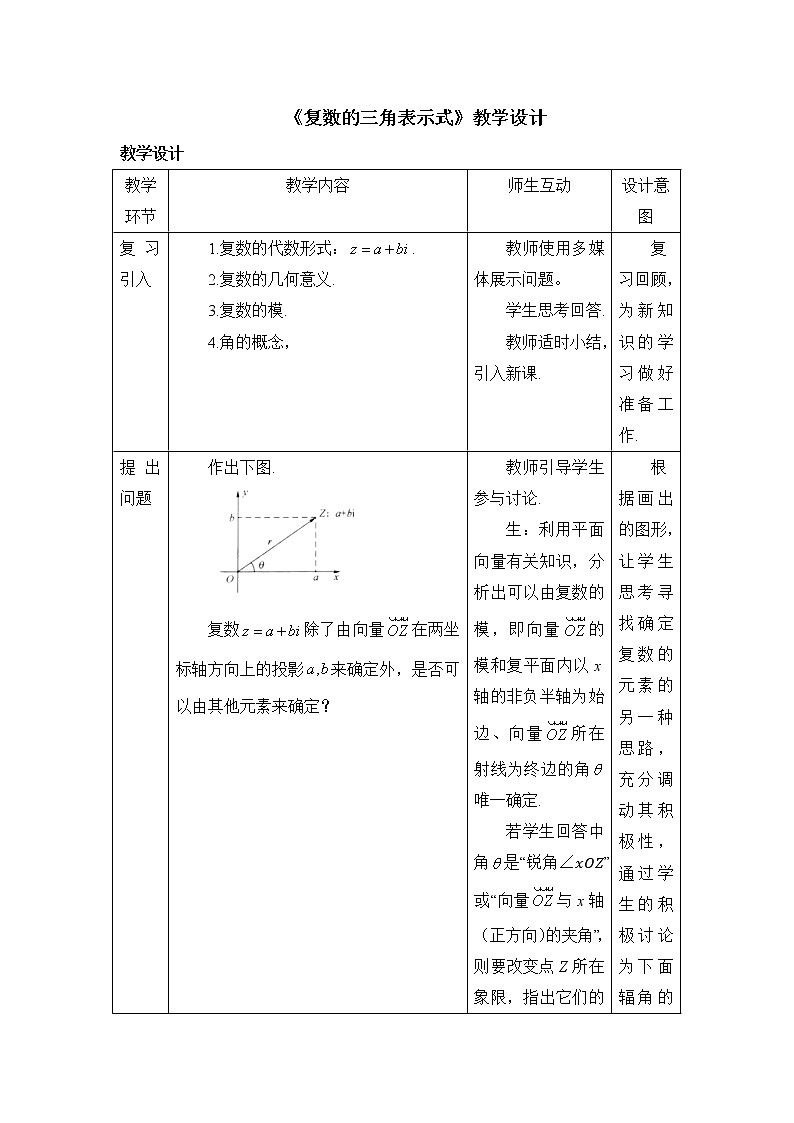
提出问题
作出下图.
复数除了由向量在两坐标轴方向上的投影来确定外,是否可以由其他元素来确定?
教师引导学生参与讨论.
生:利用平面向量有关知识,分析出可以由复数的模,即向量的模和复平面内以x轴的非负半轴为始边、向量所在射线为终边的角唯一确定.
若学生回答中角是“锐角∠???”或“向量与x轴(正方向)的夹角”,则要改变点Z所在象限,指出它们的不完善性,从而避免学生对辐角产生误解.
根据画出的图形,让学生思考寻找确定复数的元素的另一种思路,充分调动其积极性,通过学生的积极讨论为下面辐角的学习打下基础.
探究新知
1.复数的三角形式.
提出问题:有序实数对唯一确定个复数,如何用r和表示出所确定的这个复数呢?
复数三角表示式的相关概念:一般地,任何一个复数都可以表示成的形式.其中,r是复数z的模;是以x轴的非负半轴为始边,向量所在射线(射线OZ)为终边的角,叫做复数的辐角.叫做复数的三角表示式.简称三角形式.
任一非零复数的辐角都有无限多个值,这些值相差的整数倍.
2.复数辐角主值的定义.
问题一:任一非零复数的辐角适合于的有几个?
问题二:两个非零复数相等的充分必要条件是它们的模与辐角分别相等吗?是它们的模与辐角主值相等吗?
3.复数0的辐角.
复数与复平面的原点O、零向量对应.由于零向量的方向是任意的,所以复数0的辐角也是任意的,其辐角主值是内的任意角.
学生继续阅读教材回答.
师:由前述图象,得出复数的实部,虚部,所以该复数为,即,此形式叫做复数的三角形式.
教师强调复数三角形式的三个特点:“一正二角三符号”.
教师提出辐角的个数问题.
学生利用三角函数的知识作出回答.
学生阅读教材回答.
教师得出结论.
辐角主值的定义及符号表示:
定义:规定在
范围内的辐角的值为辐角的主值通常记为.
学生阅读教材回答.
师:由复数辐角和辐角主值的定义,得出结论:两个非零复数相等的充分必要条件是它们的模相等,辐角的主值也相等.
师:复数0的辐角是怎样的呢?
学生思考讨论,得出结论.
通过提出问题,引导学生阅读教材,明确复数的三角形式及相关概念.
通过两个问题的思考,使学生明确复数辐角主值与辐角的区别,并掌握两个非零复数相等的充要条件体现了逻辑推理和数学抽象的核心素养.
应用举例
例1 (1)复数的一个辐角是( )
A.60-∘.
B.
C.
D.
(2)复数的辐角主值是( )
A.30-∘.
B.150°
C.
D.330°
解:(1)A(2)D
例2 画出下列复数所对应的向量,并把这些复数表示成三角形式:
(1);(2).
解:(1)复数,所对应的向量如图所示,
则
因为与对应的点在第一象限,所以,
于是.
(2)复数所对应的向量如图所示,
则,.
因为复数对应的点在第四象限,所以,
于是
.
例3 分别指出下列复数的模和一个辐角,画出它们对应的向量,并把这些复数表示成代数形式:
(1);
(2)...
解:(1)复数的模,一个辐角,对应的向量如图所示.
所以.
(2)复数
的模,一个辐角,对应的向量如图所示.
所以
.
学生思考运算回答.
教师指导总结.
判断复数的三角形式与求解复数的辐角主值,要严格按照复数的三角表示式,对于不是以复数的三角形式表示的式子,要根据复数三角形式的定义将其转化,再进一步判断.
教师让学生自行解答,找代表上台板书,全班核对.
教师强调:正确画出图形是顺利解题的关键.
针对第(2)题,教师可提问:如果辐角θ不取主值的话,该题的答案又如何呢?让学生分小组讨论,给出自已的答案(答案有无数种,只要符合条件即可).
学生自己练习,之后教师提问:
(1)在坐标轴上的复数能用三角形式表示吗?
(2)你能总结出复数的代数形式和三角形式之间的互化的步骤吗?
通过让学生对本节课所涉及的实例进行分析和解答,使学生熟悉复数三角形式的有关概念,并进步熟练掌握复数的代数形式与三角形式的互化.
巩固训练
教材第86页练习第1,2,3题.
先让学生独立思考、逐个回答,再请其他学生评价,最后教师讲解、点评.
培养解题能力,巩固所学知识.
归纳小结
1.复数三角形式的表示式.
2.复数的辐角主值与辐角.
3.复数代数形式与三角形式的互化.
小组合作总结,选出代表发表自己的收获感言.
关注与培养学生数学抽象这方面的素养.
布置作业
1.教材第89页习题7.3第1,2题.
2.教材第89页习题7.3第5题(选做题).
学生独立完成.
通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
7.3.1复数的三角表示式
一、复习引入
二、提出问题
三、探究新知
1.复数的三角形式
一般地,任何一个复数都可以表示成的形式其中,r是复数z的模;是以x轴的非负半轴为始边,向量所在射线(射线OZ)为终边的角,叫做复数的辐角叫做复数的三角表示式简称三角形式
2.复数辐角主值的定义
规定在范围内的辐角的值为辐角的主值
3.复数0的辐角
四、应用举例
例1
例2
例3
五、巩固训练
六、归纳小结
七、布置作业
高中数学人教A版 (2019)必修 第二册7.3* 复数的三角表示教案: 这是一份高中数学人教A版 (2019)必修 第二册7.3* 复数的三角表示教案,共2页。
数学必修 第二册7.3* 复数的三角表示教学设计: 这是一份数学必修 第二册7.3* 复数的三角表示教学设计,共2页。
高中7.3* 复数的三角表示教学设计: 这是一份高中7.3* 复数的三角表示教学设计,共13页。教案主要包含了本节内容分析,学情整体分析,教学活动准备,教学活动设计等内容,欢迎下载使用。













