2023泸州泸县四中高二上学期期中考试数学（理）试题含答案

这是一份2023泸州泸县四中高二上学期期中考试数学（理）试题含答案，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
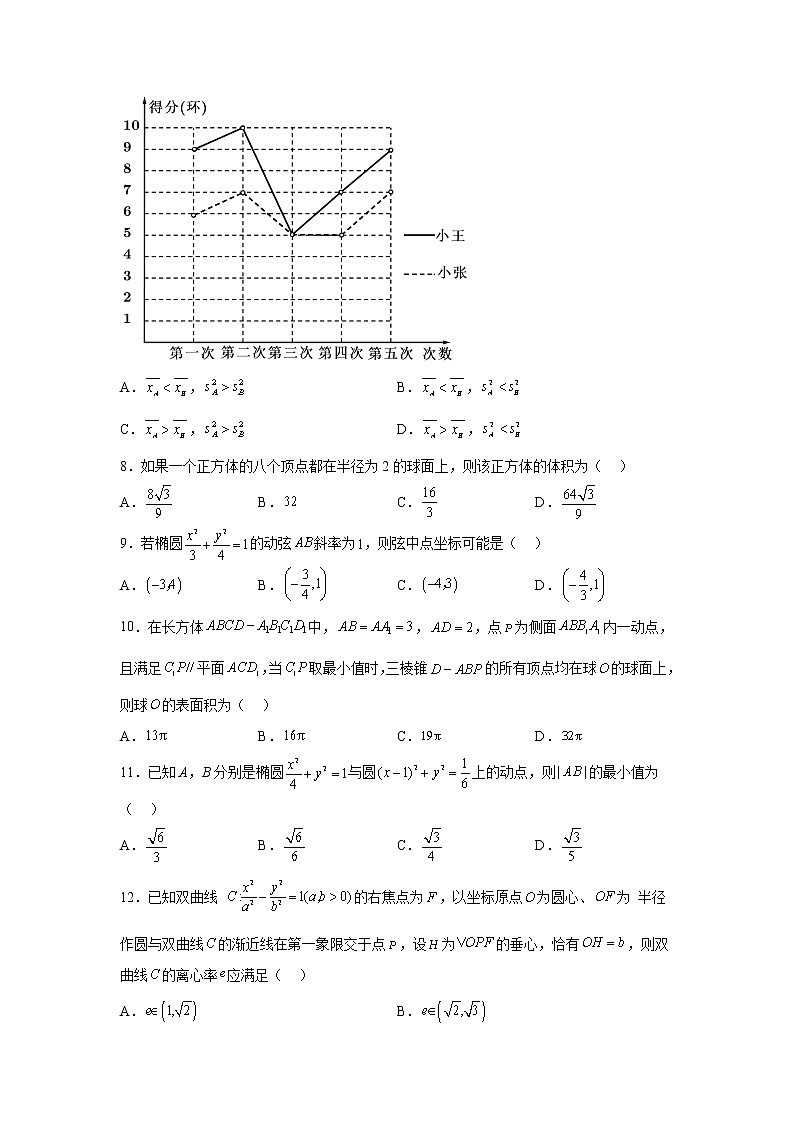
泸县四中2022-2023学年高二上期中考试理科数学考试时间：120分钟     满分：150分  第I卷  选择题（60分）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。1．为了解名学生的学习情况，现采用系统抽样的方法，从中抽取容量为的样本，则分段的间隔为（    ）A． B． C． D．2．某社区义工队有24名成员，他们年龄的茎叶图如图所示，先把他们按年龄从小到大编号为1至24号，再用系统抽样方法抽出6人组成一个工作小组．则这个小组中年龄不超过55岁的人数为（    ）A．1 B．2 C．3 D．43．设满足约束条件，则的最小值为（    ）A． B． C． D．4．下列命题中，真命题是（    ）A． B．C．的充要条件是 D．是的充分条件5．若，则下列结论正确的是（    ）A． B． C． D．6．直线被圆所截得的弦长是（    ）A． B． C． D．7．小王与小张二人参加某射击比赛，二人在选拔赛的五次测试的得分情况如图所示.设小王与小张这五次射击成绩的平均数分别为和，方差分别为和，则（    ）A．， B．，C．， D．，8．如果一个正方体的八个顶点都在半径为2的球面上，则该正方体的体积为（    ）A． B． C． D．9．若椭圆​的动弦​斜率为​，则弦中点坐标可能是（    ）A．​ B． C．​ D．​10．在长方体中，，，点为侧面内一动点，且满足平面，当取最小值时，三棱锥的所有顶点均在球的球面上，则球的表面积为（    ）A． B． C． D．11．已知A，B分别是椭圆与圆上的动点，则的最小值为（    ）A． B． C． D．12．已知双曲线 的右焦点为，以坐标原点为圆心、为 半径作圆与双曲线的渐近线在第一象限交于点，设为的垂心，恰有，则双曲线的离心率应满足（    ）A． B．C． D．第II卷   非选择题（90分）二、填空题(5分每题，共20分)13．三进制数化为六进制数为，则_______．14．若 ​与​相外切， 则实数​____________.15．已知直线与曲线有两个不同的交点，则实数的取值范围是________.16．已知，，且，则的最小值是_______.三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答17．（10分）求下列不等式的解集：(1)；                    (2).  18．（12分）已知圆C：，直线l：．(1)求证：直线l与圆C恒相交；(2)当时，过圆C上点作圆的切线交直线l于点P，Q为圆C上的动点，求的取值范围．   19．（12分）已知长轴长为的椭圆的一个焦点为．(1)求椭圆C的方程；(2)若斜率为l的直线交椭圆于，两点，且，求直线的方程． 20．（12分）如图，在直角梯形中，为的中点，沿将折起，使得点到点的位置，且为的中点，为边上的动点（与点不重合）.(1)证明：平面平面；(2)已知二面角的余弦值为，试确定点位置，并说明理由.      21．（12分）设双曲线 ​的上焦点为，过​且平行于​轴的弦其长为．(1)求双曲线​的标准方程及实轴长；(2)直线与双曲线​交于​两点，且满足，求实数​的值．  22．（12分）设椭圆 ​的右焦点为​，右顶点为​，上顶点为​. 已知椭圆 的短轴长为​，且有​.(1)求椭圆的方程;(2)设 ​为该椭圆上两动点，​分别为​在​轴上的射影，而直线​、​的斜率分别为、​，满足​，其中​为原点. 记​和​的面积之和为​，求​的最大值    泸县四中2022-2023学年高二上期中考试理科数学参考答案与评分标准1．A  2．B  3．C  4．D  5．C  6．D  7．C  8．D  9．B  10．A   11．B  12．B13．9     14．11   15．        16．17．（1）由，得解得或...................3分所以不等式的解集为或；..................5分（2）由，可得，..................6分等价于，解得，..................9分所以不等式的解集为．..................10分18．（1）∵直线l的方程可化为m(x＋2y－7)＋2x＋y－8＝0，故l恒过点A(3，2)．........3分∵(3－2)2＋(2－3)2＝2＜4，即点A在圆C内，..................4分∴直线l与圆C恒相交．..................5分（2）圆心是,圆半径为2,因此过的切线方程为x＝0．又当m＝1时，l：x＋y＝5，∴联立，得交点P（0，5），..................8分∴，圆半径为2，  ∴．..................12分19．（1）由题意，，， ∴， ∴椭圆的方程为．..................4分（2）设直线的方程为，点，联立方程组化简，得，，即，  ..................7分      且，，.................8分∴.................10分解得，符合题意，..................11分∴直线的方程为或...................12分20．（1）因为平面，所以平面.所以∵所以平面.因为平面，所以.因为，所以.因为平面，所以平面.因为平面，所以平面平面...................4分（2）过作于.因为，所以.由（1）知平面，所以平面.过作于，连接.因为平面平面，所以.因为平面，所以平面.因为平面平面，所以，所以是二面角的平面角...................8分因为，则.在Rt中，设，则由RtRt，得，所以.则.因为二面角的余弦值为，即，则，解得.此时为的中点..................12分21．（1）解: 双曲线的上焦点的坐标为，取，代入，得，，，故的标准方程为，双曲线的实轴长也为．..................6分（2）解：联立 ，可得，且，② ，将① 式、② 式代入， 有， 且满足．..................12分22．（1）由题设知 ​，设椭圆半焦距为​，则，，，，又,则​，又​，可得​，则椭圆的方程为​...................4分（2）联立 ​，得，..................5分可得 ​，，..................6分而的面积​，..................8分同理，的面积为​，故​，而 ​..................9分​令 ​，则​，..................11分故当 ​，即​或​时，​取到最大值​..................12分