

2020-2021学年宁夏中卫市沙坡头区中宁三中八年级(下)期末数学试卷
展开
这是一份2020-2021学年宁夏中卫市沙坡头区中宁三中八年级(下)期末数学试卷,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.(3分)若a>b,则下列关系式不成立的是( )
A.a﹣5>b﹣5B.6a>6bC.﹣a>﹣bD.a﹣b>0
2.(3分)若一个等腰三角形的两边长分别为2,4,则第三边的长为( )
A.2B.3C.4D.2或4
3.(3分)下面图形中,是中心对称图形的是( )
A.B.
C.D.
4.(3分)在代数式32a,a+b2,-x+14-x,12xy+x2y,4abπ,x2yx中,分式有( )
A.2个B.3个C.4个D.5个
5.(3分)下列各式由左边到右边的变形中,是分解因式的是( )
A.a(x﹣y)=ax﹣ayB.x2﹣4x+3=x(x﹣4)+3
C.a2﹣b2=(a+b)(a﹣b)D.a2+1=a(a+1a)
6.(3分)下列计算正确的是( )
A.1+1a=2aB.1a-b-1b-a=0
C.a÷b•1b=aD.-a-ba+b=-1
7.(3分)如图,在Rt△ABC中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得△A′B′O,那么点A′的坐标为( )
A.(3,1)B.(1,3)C.(﹣1,3)D.(3,﹣1)
8.(3分)若不等式组x+a≥05-3x>x-3有解,则a的取值范围是( )
A.a≤﹣2B.a≥﹣2C.a<﹣2D.a>﹣2
二、填空题(本题共计8小题,每题3分,共计24分)
9.(3分)当x= 时,分式2x+13x-4无意义.
10.(3分)因式分解:a2﹣4b2= .
11.(3分)如图所示,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件 . (只需填一个你认为正确的条件即可)
12.(3分)a与2b互为相反数,则a2+4ab+4b2= .
13.(3分)一个多边形的内角和等于1260°,则这个多边形是 边形.
14.(3分)如图,在△ABC中,AC=5cm,线段AB的垂直平分线交AC于点N,△BCN的周长是8cm,则BC= .
15.(3分)不等式组1<12x﹣2≤2的所有整数解的和为 .
16.(3分)如图,一次函数y=kx+b的图象经过点A(﹣1,2),则不等式kx+b<2的解集为 .
三、解答题(本题共计10小题,共计72分)
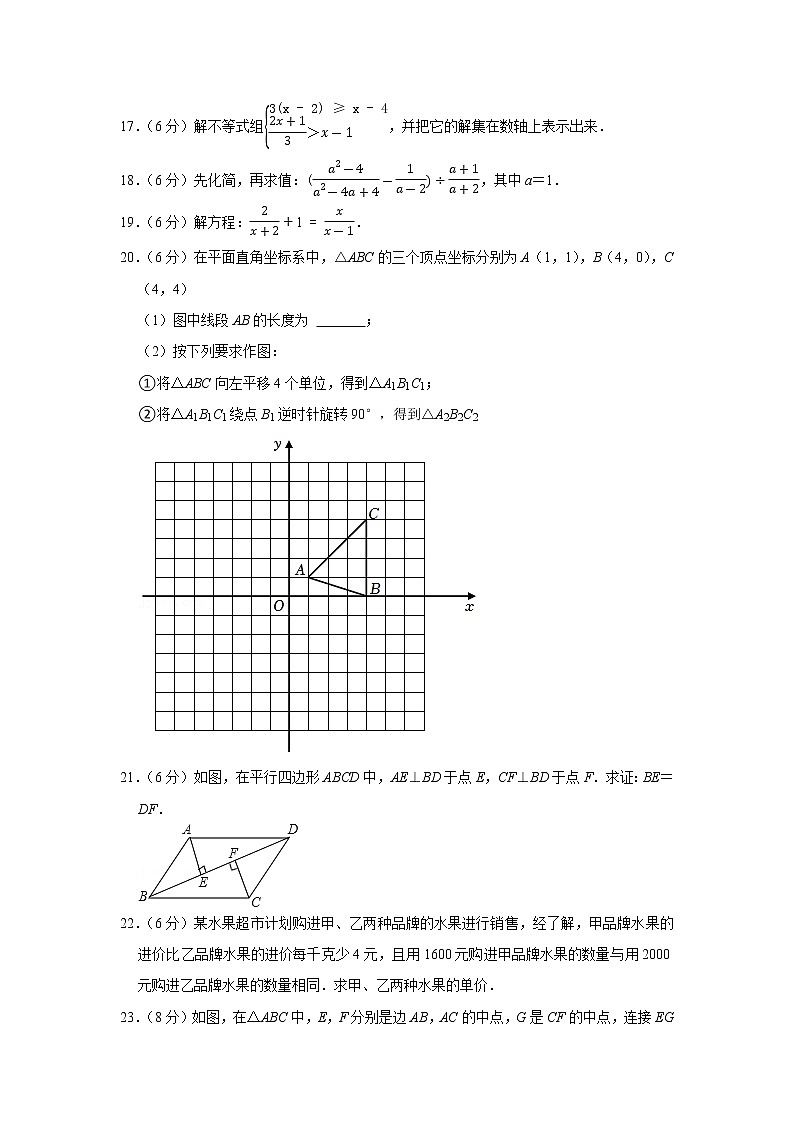
17.(6分)解不等式组3(x-2)≥x-42x+13>x-1,并把它的解集在数轴上表示出来.
18.(6分)先化简,再求值:(a2-4a2-4a+4-1a-2)÷a+1a+2,其中a=1.
19.(6分)解方程:2x+2+1=xx-1.
20.(6分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4)
(1)图中线段AB的长度为 ;
(2)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2
21.(6分)如图,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F.求证:BE=DF.
22.(6分)某水果超市计划购进甲、乙两种品牌的水果进行销售,经了解,甲品牌水果的进价比乙品牌水果的进价每千克少4元,且用1600元购进甲品牌水果的数量与用2000元购进乙品牌水果的数量相同.求甲、乙两种水果的单价.
23.(8分)如图,在△ABC中,E,F分别是边AB,AC的中点,G是CF的中点,连接EG并延长,交BC的延长线于点D,求证:BC=2CD.
24.(8分)已知:如图,平行四边形ABCD的对角线AC与BD相交于点O,E是BC的中点,连接OE并延长使EF=OE,连接BF、CF.
求证:(1)OB=CF;
(2)四边形OFCD是平行四边形.
25.(10分)现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分别直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
26.(10分)如图,在四边形ABCD中,AD∥BC,AD=15米,CD=24米,BC=46米,∠D=150°,点P在BC上由点C向点B出发,速度为每秒4米;点Q在边AD上,同时由点A向点D运动,速度为每秒1米,当点P运动到B点时,P、Q同时停止运动,连接PQ,设运动时间为t秒.
(1)当t为何值时PQ∥CD?
(2)设四边形PCDQ的面积为S,求S与t之间的函数关系式;
(3)是否存在某一时刻t,使点D在线段PC的垂直平分线上?并求出此刻t的值.
2020-2021学年宁夏中卫市沙坡头区中宁三中八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本题共计8小题,每题3分,共计24分)
1.(3分)若a>b,则下列关系式不成立的是( )
A.a﹣5>b﹣5B.6a>6bC.﹣a>﹣bD.a﹣b>0
【解答】解:A、若a>b,则a﹣5>b﹣5,原变形成立,故本选项不符合题意;
B、若a>b,则6a>6b,原变形成立,故本选项不符合题意;
C、若a>b,则﹣a<﹣b,原变形不成立,故本选项符合题意;
D、若a>b,则a+2>b+2,原变形成立,故本选项不符合题意;
故选:C.
2.(3分)若一个等腰三角形的两边长分别为2,4,则第三边的长为( )
A.2B.3C.4D.2或4
【解答】解:①4是腰长时,三角形的三边分别为4、4、2,
能组成三角形,
所以,第三边为4;
②4是底边时,三角形的三边分别为2、2、4,
∵2+2=4,
∴不能组成三角形,
综上所述,第三边为4.
故选:C.
3.(3分)下面图形中,是中心对称图形的是( )
A.B.
C.D.
【解答】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意;
D.不是中心对称图形,故本选项不符合题意.
故选:C.
4.(3分)在代数式32a,a+b2,-x+14-x,12xy+x2y,4abπ,x2yx中,分式有( )
A.2个B.3个C.4个D.5个
【解答】解:在32a,a+b2,-x+14-x,12xy+x2y,4abπ,x2yx中,分式有32a,-x+14-x,x2yx这3个,
故选:B.
5.(3分)下列各式由左边到右边的变形中,是分解因式的是( )
A.a(x﹣y)=ax﹣ayB.x2﹣4x+3=x(x﹣4)+3
C.a2﹣b2=(a+b)(a﹣b)D.a2+1=a(a+1a)
【解答】解:A、a(x﹣y)=ax﹣ay,是整式乘法运算,故此选项错误;
B、x2﹣4x+3=x(x﹣4)+3,不符合分解因式的定义,故此选项错误;
C、a2﹣b2=(a+b)(a﹣b),是分解因式,符合题意;
D、a2+1=a(a+1a),不符合分解因式的定义,故此选项错误;
故选:C.
6.(3分)下列计算正确的是( )
A.1+1a=2aB.1a-b-1b-a=0
C.a÷b•1b=aD.-a-ba+b=-1
【解答】解:(A)原式=a+1a,故A错误.
(B)原式=1a-b+1a-b=2a-b,故B错误.
(C)原式=a×1b•1b=ab2,故C错误.
故选:D.
7.(3分)如图,在Rt△ABC中,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得△A′B′O,那么点A′的坐标为( )
A.(3,1)B.(1,3)C.(﹣1,3)D.(3,﹣1)
【解答】解:∵OA=2,AB=1,
∴OB=OA2-AB2=3,由图知A点的坐标为(3,1),根据旋转中心O,旋转方向顺时针,旋转角度90°,画图,从而得A′点坐标为(﹣1,3).
故选:C.
8.(3分)若不等式组x+a≥05-3x>x-3有解,则a的取值范围是( )
A.a≤﹣2B.a≥﹣2C.a<﹣2D.a>﹣2
【解答】解:x+a≥0①5-3x>x-3②,
解不等式①,得x≥﹣a,
解不等式②,得x<2,
∵不等式组x+a≥05-3x>x-3有解,
∴﹣a<2,
解得:a>﹣2,
故选:D.
二、填空题(本题共计8小题,每题3分,共计24分)
9.(3分)当x= 43 时,分式2x+13x-4无意义.
【解答】解:分式无意义,则3x﹣4=0,
∴x=43.
10.(3分)因式分解:a2﹣4b2= (a+2b)(a﹣2b) .
【解答】解:原式=a2﹣(2b)2=(a+2b)(a﹣2b).
故答案是:(a+2b)(a﹣2b).
11.(3分)如图所示,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件 AD=BC(或AB∥CD) . (只需填一个你认为正确的条件即可)
【解答】解:根据平行四边形的判定方法,知
需要增加的条件是AD=BC或AB∥CD或∠A=∠C或∠B=∠D.
故答案为AD=BC(或AB∥CD).
12.(3分)a与2b互为相反数,则a2+4ab+4b2= 0 .
【解答】解:由a与2b互为相反数,得到a+2b=0,
则原式=(a+2b)2=0.
故答案为:0.
13.(3分)一个多边形的内角和等于1260°,则这个多边形是 九 边形.
【解答】解:根据题意,得
(n﹣2)•180=1260,
解得n=9.
14.(3分)如图,在△ABC中,AC=5cm,线段AB的垂直平分线交AC于点N,△BCN的周长是8cm,则BC= 3cm .
【解答】解:∵MN是线段AB的垂直平分线,
∴NA=NB,
∴AC=NA+NC=NB+NC=5,
∵△BCN的周长是8,
∴NB+NC+BC=8,
∴BC=8﹣5=3(cm),
故答案为:3cm.
15.(3分)不等式组1<12x﹣2≤2的所有整数解的和为 15 .
【解答】解:由题意可得12x-2>1①12x-2≤2②,
解不等式①,得:x>6,
解不等式②,得:x≤8,
则不等式组的解集为6<x≤8,
所以不等式组的所有整数解的和为7+8=15,
故答案为:15.
16.(3分)如图,一次函数y=kx+b的图象经过点A(﹣1,2),则不等式kx+b<2的解集为 x>﹣1 .
【解答】解:∵次函数y=kx+b的图象经过第一、二、四象限,
∴y随x的增大而减小,
∵点A(﹣1,2)在直线y=kx+b上,
∴当x=﹣1时,y=kx+b=2,
∴当x>﹣1时,kx+b<2,
即不等式kx+b<2的解集为x>﹣1.
故答案为x>﹣1.
三、解答题(本题共计10小题,共计72分)
17.(6分)解不等式组3(x-2)≥x-42x+13>x-1,并把它的解集在数轴上表示出来.
【解答】解:∵解不等式3(x﹣2)≥x﹣4得:x≥1,
解不等式2x+13>x﹣1得:x<4,
∴不等式组的解集是1≤x<4,
在数轴上表示不等式组的解集是:.
18.(6分)先化简,再求值:(a2-4a2-4a+4-1a-2)÷a+1a+2,其中a=1.
【解答】解:原式=[(a+2)(a-2)(a-2)2-1a-2]÷a+1a+2
=(a+2a-2-1a-2)÷a+1a+2
=a+1a-2•a+2a+1
=a+2a-2,
当a=1时,原式=1+21-2=-3.
19.(6分)解方程:2x+2+1=xx-1.
【解答】解:2x+2+1=xx-1,
方程两边同时乘以(x+2)(x﹣1),得
2(x﹣1)+(x+2)(x﹣1)=x(x+2),
∴x=4,
经检验x=4是方程的解;
∴方程的解为x=4;
20.(6分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4)
(1)图中线段AB的长度为 10 ;
(2)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2
【解答】解:(1)∵A(1,1),B(4,0),
∴AB=(1-4)2+(1-0)2=10;
故答案为:10;
(2)①如图所示,△A1B1C1即为所求.
②如图所示,△A2B2C2即为所求.
21.(6分)如图,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F.求证:BE=DF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中
∠ABE=∠CDF∠AEB=∠CFDAB=DC,
∴△ABE≌△CDF(AAS),
∴BE=DF.
22.(6分)某水果超市计划购进甲、乙两种品牌的水果进行销售,经了解,甲品牌水果的进价比乙品牌水果的进价每千克少4元,且用1600元购进甲品牌水果的数量与用2000元购进乙品牌水果的数量相同.求甲、乙两种水果的单价.
【解答】解:设甲种品牌的水果的单价为x元/千克,则乙种品牌的水果的单价为(x+4)元/千克.
根据题意得:1600x=2000x+4,
解得x=16,
经检验,x=16是分式方程的解.
则乙种品牌的水果的单价为16+4=20(元/千克).
答:甲种品牌的水果的单价为16元/千克,乙种品牌的水果的单价为20元/千克.
23.(8分)如图,在△ABC中,E,F分别是边AB,AC的中点,G是CF的中点,连接EG并延长,交BC的延长线于点D,求证:BC=2CD.
【解答】证明:∵E,F分别是边AB,AC的中点,
∴EF是△ABC的中位线.
∴EF∥BC,BC=2EF,
∴∠DCG=∠EFG.
∵G是CF的中点,
∴GC=GF,
在△GCD和△GFE中,
∠DCG=∠EFGGC=GF∠CGD=∠FGE,
∴△GCD≌△GFE(ASA),
∴EF=CD,
∴BC=2CD.
24.(8分)已知:如图,平行四边形ABCD的对角线AC与BD相交于点O,E是BC的中点,连接OE并延长使EF=OE,连接BF、CF.
求证:(1)OB=CF;
(2)四边形OFCD是平行四边形.
【解答】证明:(1)∵E是BC中点,
∴BE=CE,
∵EF=OE,
∴四边形OBFC是平行四边形,
∴OB=CF;
(2)∵四边形ABCD是平行四边形,
∴BO=DO,
∵BE=CE,
∴OE∥CD,
即OF∥CD,
∵四边形OBFC是平行四边形,
∴OB∥CF,
∴OD∥CF,
∴四边形OFCD是平行四边形.
方法二:∵四边形ABCD是平行四边形,
∴O为BD中点,
∵E是BC的中点,
∴OE为△BCD的中位线,
∴OE∥CD,OE=12CD,
∵EF=OE,
∴OE=12OF,
∴OF=CD且OF∥CD,
∴四边形OFCD是平行四边形.
25.(10分)现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分别直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
【解答】解:(1)由题意可得,
y甲=22+15(x﹣1)=15x+7,
y乙=16x+3;
(2)x>1时,令y甲<y乙,
即15x+7<16x+3
解得:x>4,
令y甲=y乙,
即15x+7=16x+3,
解得:x=4,
令y甲>y乙,
即15x+7>16x+3,
解得:x<4,
综上可知:当1<x<4时,选乙快递公司省钱;当x=4时,选甲、乙两家快递公司快递费一样多;当x>4时,选甲快递公司省钱.
26.(10分)如图,在四边形ABCD中,AD∥BC,AD=15米,CD=24米,BC=46米,∠D=150°,点P在BC上由点C向点B出发,速度为每秒4米;点Q在边AD上,同时由点A向点D运动,速度为每秒1米,当点P运动到B点时,P、Q同时停止运动,连接PQ,设运动时间为t秒.
(1)当t为何值时PQ∥CD?
(2)设四边形PCDQ的面积为S,求S与t之间的函数关系式;
(3)是否存在某一时刻t,使点D在线段PC的垂直平分线上?并求出此刻t的值.
【解答】解:(1)∵PQ∥CD,AD∥BC,
∴四边形PCDQ是平行四边形,
∴QD=PC,
∴15﹣t=4t,
∴t=3;
(2)存在,
如图,过点D作DH⊥BC于H,
∵AD∥BC,
∴∠ADC+∠C=180°,
∴∠C=30°,
∴DH=12CD=12(米),
∴S=12×DH×(QD+PC)=6(15﹣t+4t)=90+18t;
(3)∵DH⊥BC,DC=24米,DH=12米,
∴CH=DC2-DH2=576-144=123(米),
∵点D在线段PC的垂直平分线上,
∴CP=2CH=243(米),
∴t=2434=63(秒).
:43:25;
相关试卷
这是一份宁夏_中卫市中宁县2024年九年级中考第三次联考数学试卷,共4页。
这是一份2022-2023学年宁夏中卫市中宁县八年级(下)期末数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份宁夏回族自治区中卫市中宁县2022-2023学年八年级下学期期末质量监测数学试卷,共6页。








