中考数学压轴题--二次函数--专题06 费马点求最小值

中考数学压轴题--二次函数

第6节  费马点求最小值

          内容导航

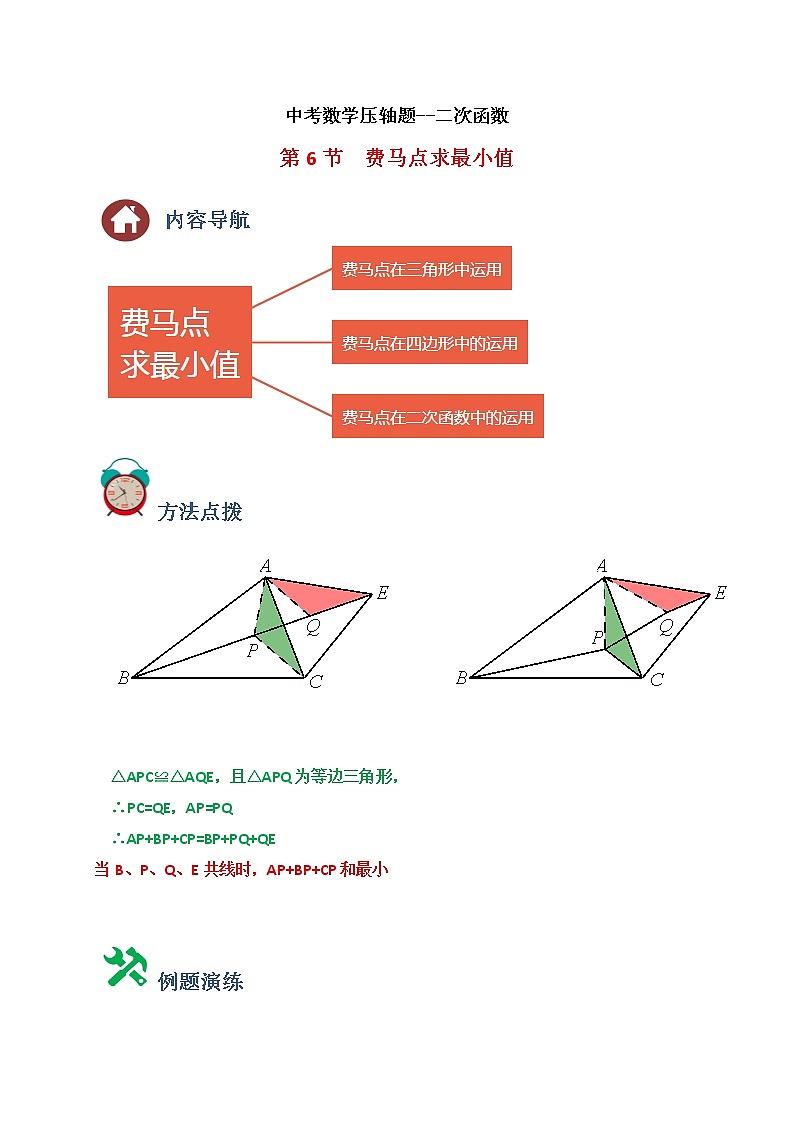
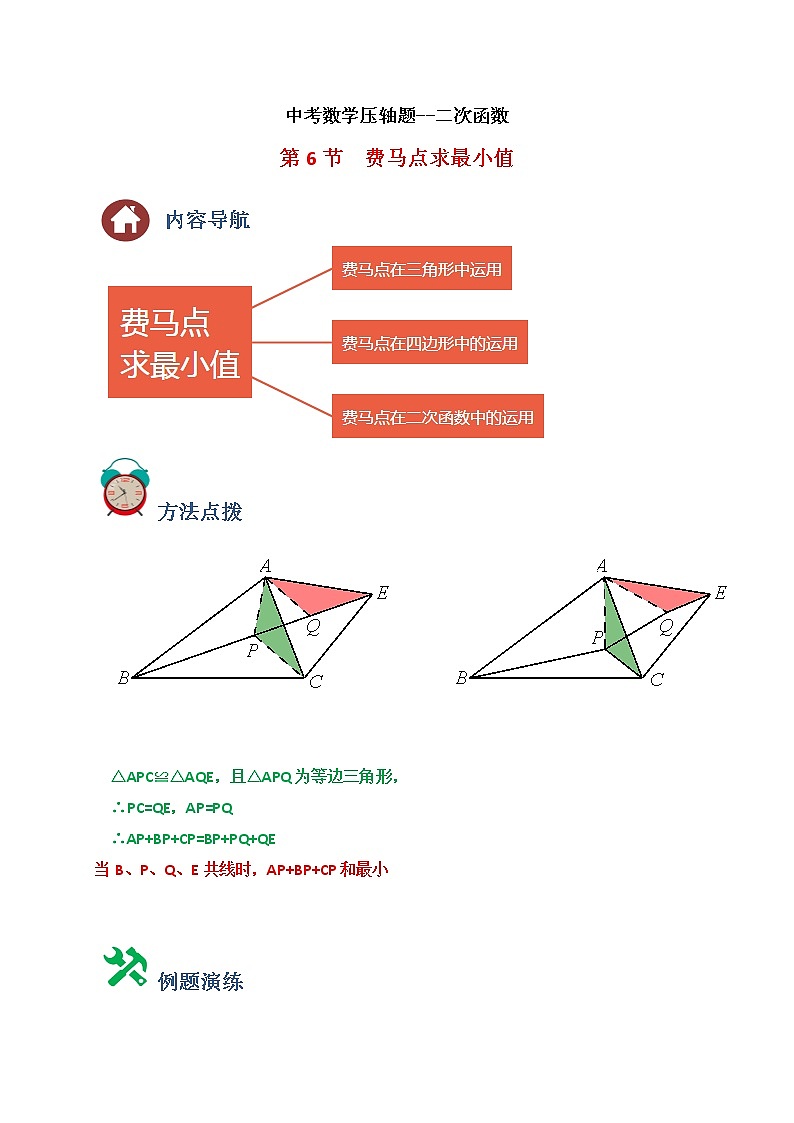
方法点拨

△APC≌△AQE，且△APQ为等边三角形，

∴PC=QE，AP=PQ

∴AP+BP+CP=BP+PQ+QE
当B、P、Q、E共线时，AP+BP+CP和最小

       例题演练

题组1：费马点在三角形中运用

例1．如图，在△ABC中，P为平面内一点，连结PA，PB，PC，分别以PC和AC为一边向右作等边三角形△PCM和△ACD．

【探究】求证：PM＝PC，MD＝PA

【应用】若BC＝a，AC＝b，∠ACB＝60°，则PA+PB+PC的最小值是　   　（用a，b表示）

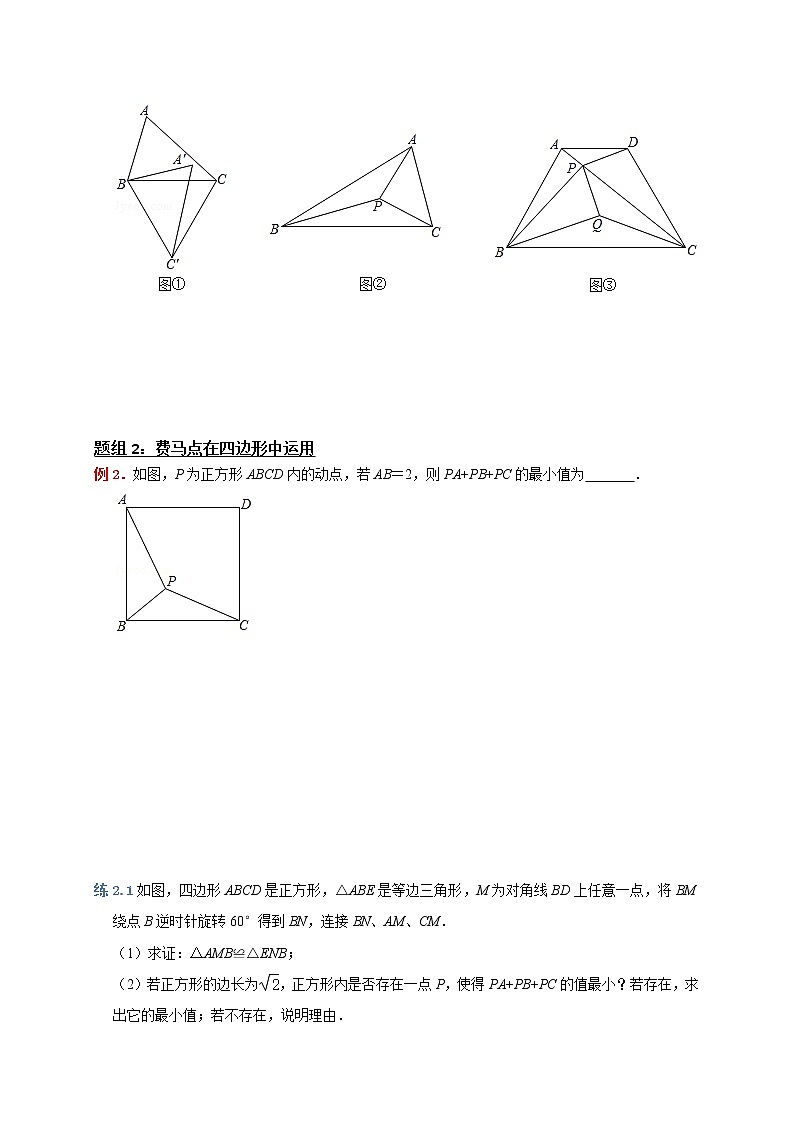
练1.1问题提出

（1）如图①，在△ABC中，BC＝2，将△ABC绕点B顺时针旋转60°得到△A′B′C′，则CC′＝　   　；

问题探究

（2）如图②，在△ABC中，AB＝BC＝3，∠ABC＝30°，点P为△ABC内一点，连接PA、PB、PC，求PA+PB+PC的最小值，并说明理由；

问题解决

（3）如图③，在四边形ABCD中，AD∥BC，AB＝6，AD＝4，∠ABC＝∠BCD＝60°．在四边形ABCD内部有一点，满足∠APD＝120°，连接BP、CP，点Q为△BPC内的任意一点，是否存在一点P和一点Q，使得PQ+BQ+CQ有最小值？若存在，请求出这个最小值；若不存在，请说明理由．

题组2：费马点在四边形中运用

例2．如图，P为正方形ABCD内的动点，若AB＝2，则PA+PB+PC的最小值为　   　．

练2.1如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD上任意一点，将BM绕点B逆时针旋转60°得到BN，连接BN、AM、CM．

（1）求证：△AMB≌△ENB；

（2）若正方形的边长为，正方形内是否存在一点P，使得PA+PB+PC的值最小？若存在，求出它的最小值；若不存在，说明理由．

例3．如图，在平面直角坐标系xOy中，点B的坐标为（0，2），点D在x轴的正半轴上，∠ODB＝30°，OE为△BOD的中线，过B、E两点的抛物线与x轴相交于A、F两点（A在F的左侧）．

（1）求抛物线的解析式；

（2）等边△OMN的顶点M、N在线段AE上，求AE及AM的长；

（3）点P为△ABO内的一个动点，设m＝PA+PB+PO，请直接写出m的最小值，以及m取得最小值时，线段AP的长．

练3.1如图，抛物线y＝ax2+bx+过点A（1，0），B（5，0），与y轴相交于点C．

（1）求抛物线的解析式；

（2）定义：平面上的任一点到二次函数图象上与它横坐标相同的点的距离，称为点到二次函数图象的垂直距离．如：点O到二次函数图象的垂直距离是线段OC的长．已知点E为抛物线对称轴上的一点，且在x轴上方，点F为平面内一点，当以A，B，E，F为顶点的四边形是边长为4的菱形时，请求出点F到二次函数图象的垂直距离．

（3）在（2）中，当点F到二次函数图象的垂直距离最小时，在以A，B，E，F为顶点的菱形内部是否存在点Q，使得AQ，BQ，FQ之和最小，若存在，请求出最小值；若不存在，请说明理由．