河南省郑州市第二初级中学2022-2023学年九年级上学期期中考试数学试卷（含答案）

2022-2023学年河南省郑州二中九年级（上）期中数学试卷

一、选择题。（30分）

1．（3分）一个几何体如图所示，它的左视图是（　　）

A． B． C． D．

2．（3分）方程x2﹣3x+1＝0的根的情况是（　　）

A．有两个相等实数根 B．有两个不相等实数根 

C．没有实数根 D．无法判断

3．（3分）如图是超市的两个摇奖转盘，只有当两个转盘指针同时指在偶数上时才能获一等奖，则摇奖人中一等奖的概率是（　　）

A． B． C． D．

4．（3分）下列命题中正确的是（　　）

A．有一组邻边相等的四边形是菱形 

B．有一个角是直角的平行四边形是矩形 

C．对角线垂直的平行四边形是正方形 

D．一组对边平行的四边形是平行四边形

5．（3分）如图，AB∥CD∥EF，AF与BE相交于点G，GD＝1，DF＝5（　　）

A．3：5 B．1：3 C．5：3 D．2：3

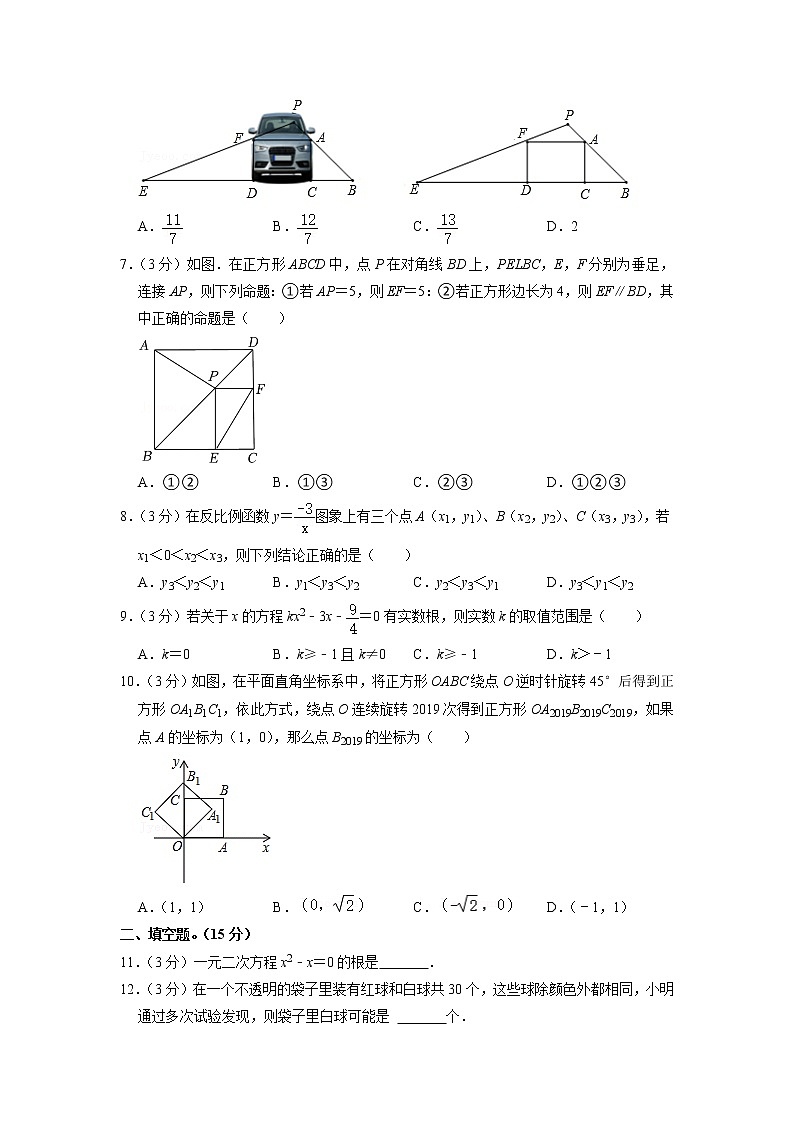
6．（3分）如图，EB为驾驶员的盲区，驾驶员的眼睛点P处与地面BE的距离为1.6米，且满足3FD＝2FA，若盲区EB的长度是6米（　　）米．

A． B． C． D．2

7．（3分）如图．在正方形ABCD中，点P在对角线BD上，PELBC，E，F分别为垂足，连接AP，则下列命题：①若AP＝5，则EF＝5：②若正方形边长为4，则EF∥BD，其中正确的命题是（　　）

A．①② B．①③ C．②③ D．①②③

8．（3分）在反比例函数y＝图象上有三个点A（x1，y1）、B（x2，y2）、C（x3，y3），若x1＜0＜x2＜x3，则下列结论正确的是（　　）

A．y3＜y2＜y1 B．y1＜y3＜y2 C．y2＜y3＜y1 D．y3＜y1＜y2

9．（3分）若关于x的方程kx2﹣3x﹣＝0有实数根，则实数k的取值范围是（　　）

A．k＝0 B．k≥﹣1且k≠0 C．k≥﹣1 D．k＞﹣1

10．（3分）如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2019次得到正方形OA2019B2019C2019，如果点A的坐标为（1，0），那么点B2019的坐标为（　　）

A．（1，1） B． C． D．（﹣1，1）

二、填空题。（15分）

11．（3分）一元二次方程x2﹣x＝0的根是　   　．

12．（3分）在一个不透明的袋子里装有红球和白球共30个，这些球除颜色外都相同，小明通过多次试验发现，则袋子里白球可能是 　   　个．

13．（3分）如图，乐器上的一根弦AB＝80cm，两个端点A，支撑点C是靠近点B的黄金分割点，则支撑点C到端点B的距离是 　   　．

14．（3分）如图，Rt△ABC中，∠ACB＝90°，BC＝12，D是AB边的中点（点P不与B、C重合），若以D、C、P为顶点的三角形与△ABC相似，则线段PC＝　   　．

15．（3分）如图，矩形ABCD中，AB＝2，点E在边BC上，把△DEC沿DE翻折后，则CE的长为　   　．

三、解答题。

16．（8分）用适当的方法解下列方程：

（1）x2﹣2x＝4；

（2）2x（x﹣3）＝3﹣x．

17．（9分）某小区为了促进生活垃圾的分类处理，将生活垃圾分为厨余、可回收和其他三类，分别记为a，b，c，“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱，分别记为A，B

（1）若小明将一袋分好类的生活垃圾随机投入一类垃圾箱，请画树状图或列表求垃圾投放正确的概率；

（2）为调查居民生活垃圾分类投放情况，现随机抽取了该小区三类垃圾箱中总共100吨生活垃圾，数据统计如下表（单位：吨）：

试估计该小区居民“厨余垃圾”投放正确的概率约是多少．

18．（10分）如图，AD是等腰△ABC底边BC上的高，点O是AC中点，使AE∥BC，连接AE．

（1）求证：四边形ADCE是矩形；

（2）①若AB＝17，BC＝16，则四边形ADCE的面积＝　   　．

②若AB＝10，则BC＝　   　时，四边形ADCE是正方形．

19．（10分）如图，AB⊥BD，CD⊥BD，CD＝4，BD＝14，以P，C，D为顶点的三角形与△ABP相似时

20．（10分）某天小明和小亮去某影视基地游玩，当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上（如图）．已知小明的眼睛离地面1.6米，小明到凉亭的距离为2米，凉亭离城楼底部的距离为38米

21．（8分）如图，已知直线与双曲线，B两点，且点A的横坐标为4．

（1）求k值；

（2）直接写出当x取何值时，一次函数的值小于反比例函数的值．

22．（8分）西瓜经营户以2元/千克的价格购入一批小型西瓜，以3元/千克的价格出售，每天可以售出200千克，该经营户决定降价销售，经调查发现，每天可多售出40千克，该经销户想每天盈利224元

23．（12分）如图1，在Rt△ABC中，∠B＝90°，BC＝2，点D，AC的中点，连接DE．将△CDE绕点C逆时针方向旋转

（1）问题发现

①当α＝0°时，＝　   　；

②当α＝180°时，＝　   　；

（2）拓展探究

试判断当0°＜α＜360°时，的大小有无变化？请仅就图2的情形给出证明；

（3）问题解决

当△CDE绕点C逆时针旋转至A，B，E三点在同一条直线上时，求线段BD的长．

参考答案与试题解析

1．【解答】解：从左面看该几何体，所得到的图形如下：

故选：B．

2．【解答】解：∵a＝1，b＝﹣3，

∴Δ＝b2﹣4ac＝（﹣3）8﹣4×1×3＝5＞0，

所以方程有两个不相等的实数根．

故选：B．

3．【解答】解：方法一：由图可得，

摇奖人中一等奖的概率是：＝＝＝，

故选：B．

方法二：

在第二个扇形统计图中，4对应的圆心角是240°，4出现一次，

树状图如下所示：

由图可知，一共有6种可能性，故摇奖人中一等奖的概率是＝，

故选：B．

4．【解答】解：A、一组邻边相等的平行四边形是菱形；

B、正确；

C、对角线垂直的平行四边形是菱形；

D、两组对边平行的四边形才是平行四边形．

故选：B．

5．【解答】解：∵AB∥CD∥EF，

∴＝＝＝．

故选：A．

6．【解答】解：如图，过点P作PM⊥BE，交AF于点N，

设FA＝x米，由3FD＝2FA得x＝MN，

∵四边形ACDF是矩形，

∴AF∥CD，

∴△PAF∽△PBE，

∴＝，

即＝，

∴PN＝x，

∵PN+MN＝PM，

∴x+，

解得，x＝，

故选：B．

7．【解答】解：延长EP交AD于Q，

∵四边形ABCD为正方形，

∴AD＝CD，∠ADC＝∠C＝90°，∠BDC＝45°，

∵PF⊥CD，

∴∠DPF＝45°，

∴DF＝PF，

∵PE⊥BC，

∴PQ⊥AD，四边形CEPF为矩形，

∴∠AQP＝90°，EC＝PF＝DF，

∴∠AQP＝∠C，AQ＝FC，

∴DF＝QP，

∴CE＝QP，

在△AQP和△FCE中，

，

∴△AQP≌△FCE（SAS），

∴AP＝EF，

若AP＝5，则EF＝5；

当AP⊥BD时，AP有最小值，

∵AB＝AD＝2，

∴BD＝＝＝4，

∴AP＝BD＝2，

∵EF＝AP，

∴EF的最小值为2，故②错误；

若AP⊥BD，则∠PAQ＝45°，

∵△AQP≌△FCE，

∴∠EFC＝∠PAQ＝45°，

∵∠BDC＝45°，

∴∠EFC＝∠BDC，

∴EF∥BD，故③正确；

故选：B．

8．【解答】解：∵A（x1，y1）在反比例函数y＝图象图象上，x1＜0，

∴y8＞0，

对于反比例函数y＝，在第四象限，

∵7＜x2＜x3，

∴y6＜y3＜0，

∴y3＜y3＜y1

故选：C．

9．【解答】解：当k＝0时，方程化为﹣3x﹣，解得x＝﹣；

当k≠0时，Δ＝（﹣3）5﹣4k•（﹣）≥0，

所以k的范围为k≥﹣1．

故选：C．

10．【解答】解：∵四边形OABC是正方形，且OA＝1，

∴B（1，6），

连接OB，

由勾股定理得：OB＝，

由旋转得：OB＝OB1＝OB3＝OB3＝…＝，

∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA5B1C1，

相当于将线段OB绕点O逆时针旋转45°，依次得到∠AOB＝∠BOB5＝∠B1OB2＝…＝45°，

∴B2（0，），B8（﹣1，1），B3（﹣，0），…，

发现是4次一循环，所以2019÷8＝252…余3，

∴点B2019的坐标为（﹣，0）

故选：C．

11．【解答】解：方程变形得：x（x﹣1）＝0，

可得x＝7或x﹣1＝0，

解得：x3＝0，x2＝8．

故答案为：x1＝0，x6＝1．

12．【解答】解：由题意可得，

30×0.3＝2（个），

即袋子中白球的个数最有可能是9个，

故答案为：9．

13．【解答】解：∵点C是靠近点B的黄金分割点，

∴AC＝80×＝（40，

∴BC＝AB﹣AC＝（120﹣40）cm，

故答案为：（120﹣40）cm．

14．【解答】解：∵Rt△ABC中，∠ACB＝90°，BC＝12，

∴AB＝15，

∵D是AB边的中点，

∴CD＝BD＝AB＝6.5，

∵以D、C、P为顶点的三角形与△ABC相似，

∴∠DPC＝90°或∠CDP＝90°，

（1）若∠DPC＝90°，则DP∥AC，

∴＝＝，

∴BP＝BC＝2，

则PC＝6；

（2）若∠CDP＝90°，则△CDP∽△BCA，

∴＝，

即＝，

∴PC＝．

综上所述：PC＝6或．

故答案为：6或．

15．【解答】解：如图1中，当C′A＝C′B时．

易知HC′＝FC′＝1，在Rt△DHC′中＝，

由△DHC′∽△C′FE，可得：＝，

∴＝，

∴EF＝，

∵四边形DHFC是矩形，

∴CF＝DH＝，

∴CE＝﹣＝．

如图6中，当AB＝AC′时，此时四边形CEC′D是正方形．

当AB＝BC'＝2时，因为翻折C'D＝CD＝2、C'，而BD＝2根号5，所以这种情况不成立．

综上所述，满足条件的CE的值为2或．

16．【解答】解：（1）∵x2﹣2x＝8，

∴x2﹣2x+8＝4+1，即（x﹣6）2＝5，

则x﹣8＝±，

∴x1＝7+，x2＝4﹣；

（2）∵2x（x﹣2）＝3﹣x，

∴2x（x﹣3）+（x﹣3）＝0，

∴（x﹣5）（2x+1）＝7，

则x﹣3＝0或3x+1＝0，

解得x2＝3，x2＝﹣．

17．【解答】解：（1）如图所示：

小明将一袋分好类的生活垃圾随机投入一类垃圾箱；共有9种情况，

其中投放正确的有3种情况，

∴P（垃圾投放正确）＝＝；

（2）∵＝，

∴估计该小区“厨余垃圾”投放正确的概率约为．

18．【解答】（1）证明：∵点O是AC中点，

∴AO＝OC，

∵AE∥BC，

∴∠AEO＝∠ODC，∠EAO＝∠OCD，

∴△AOE≌△COD（AAS），

∴OE＝OD，

∴四边形ADCE是平行四边形，

∵AD是等腰△ABC底边BC上的高，

∴∠ADC＝90°，

∴四边形ADCE是矩形；

（2）①∵AD是等腰△ABC底边BC上的高，BC＝16，

∴BD＝CD＝8，AB＝AC＝17，

由勾股定理得：AD＝＝15，

∴四边形ADCE的面积是AD×DC＝15×8＝120．

②当AB＝10，BC＝10时，理由如下：

∵AB＝AC＝10，BC＝10，

∴AD＝＝DC，

∵AD⊥BC，

∴四边形ADCE是正方形；

故答案为：120；10．

19．【解答】解：设DP＝x，则BP＝BD﹣x＝14﹣x，

∵AB⊥BD于B，CD⊥BD于D，

∴∠B＝∠D＝90°，

∴当＝时，△ABP∽△CDP，即＝，

解得x＝

BP＝14﹣＝8.6；

当＝时，△ABP∽△PDC，即＝，

整理得x5﹣14x+24＝0，

解得x1＝3，x2＝12，

BP＝14﹣2＝12，BP＝14﹣12＝6，

∴当BP为8.4或8或12时，以C、D、B、A为顶点的三角形相似．

故答案为：8.4或7或12．

20．【解答】解：过点A作AM⊥EF于点M，交CD于点N，

由题意得：AN＝2米，CN＝1.2﹣1.6＝4.3（米），

∵CN∥EM，

∴△ACN∽△AEM，

∴，

∴，

∴EM＝6，

∵AB＝MF＝3.7米，

∴城楼的高度为：6+7.6﹣1.8＝5.9（米）．

21．【解答】解：（1）由x＝4，得y＝2；

（2）由图象可得在两个交点的左边，一次函数的值小于反比例函数的值，

∴x＜﹣8或0＜x＜4．

22．【解答】解：设应将每千克小型西瓜的售价降x元，则每天的销售量为（200+400x）千克，

根据题意得：（3﹣2﹣x）（200+400x）＝224，

整理得：50x5﹣25x+3＝0，

解得：x2＝0.2，x7＝0.3．

∵为了促销减少库存，

∴x＝3.3．

答：应将每千克小型西瓜的售价降0.3元．

23．【解答】解：（1）①当α＝0°时，

∵Rt△ABC中，∠B＝90°，

∴AC＝＝＝2，

∵点D、E分别是边BC，

∴CE＝AE＝AC＝BC＝8，

∴＝；

故答案为：；

②如图6﹣1中，

当α＝180°时，

可得AB∥DE，

∵，

∴＝．

故答案为：；

（2）如图2，

当0°＜α＜360°时，的大小没有变化，

∵∠ECD＝∠ACB，

∴∠ECA＝∠DCB，

又∵＝，

∴△ECA∽△DCB，

∴＝，

（3）①如图3﹣5中，当点E在AB的延长线上时，

在Rt△BCE中，CE＝，

∴BE＝＝＝3，

∴AE＝AB+BE＝5，

∵＝，

∴BD＝＝，

②如图7﹣2中，当点E在线段AB上时，

在Rt△BCE中，CE＝，

∴BE＝＝＝1，

∴AE＝4﹣5＝3，

∵＝，

∴BD＝，

综上所述，满足条件的BD的长为或．