湖南省邵阳市武冈市2022-2023学年高二上学期期中考试数学试题

展开

这是一份湖南省邵阳市武冈市2022-2023学年高二上学期期中考试数学试题，共6页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。
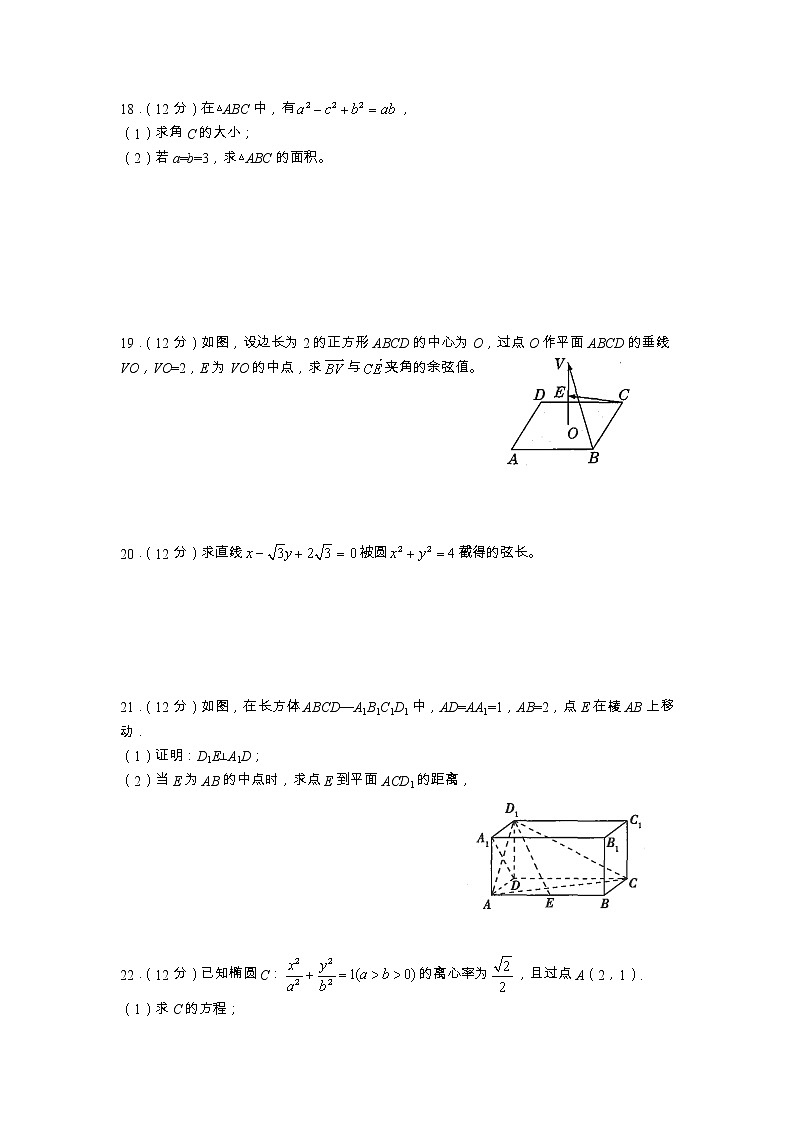
2022年下学期期中考试试卷高二数学本试卷分为问卷和答卷。考试时量为120分钟，满分150分。请将答案写在答题卡上。一、单项选择题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的）1．下列几何体中是四棱锥的是A． B． C． D．2．随机抛掷一枚质地均匀的骰子，则其向上一面的点数为偶数的概率为A． B． C． D．3．已知函数，则f(4)的值为A．2 B．4 C．8 D．244．某商场将彩电的售价选按进价提高40%，然后“八折优惠”，结果每台彩电利润为360元，那么彩电的进价是A．2000元 B．2500元 C．3000元 D．3500元5．已知=（－1，2，1）， =（3，x，1），且⊥ ，那么||等于A． B． C． D．56．已知A为抛物线C：上一点，点A到C的焦点的距离为12，到y轴的距离为9，则p=A．2 B．3 C．6 D．97．已知双曲线的一个焦点在直线上，则双曲线的渐近线方程为A． B． C． D．8．已知菱形ABCD中，∠ABC= 60°，沿对角线AC折叠之后，使得平面BAC⊥平面DAC，则二面角B—CD—A的余弦值为A．2 B．C． D．二、多项选择题（本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分）9．已知空间三点A（－1，0，1），B（－1，2，2），C（－3，0，4），则下列说法正确的是A． B． C． D．10．已知正数a，b满足a+2b=2ab，则下列说法一定正确的是A．a+2b≥4 B．a+b≥4 C．ab≥8 D．a2+4b2≥811．已知曲线C：，则下列说法正确的是A．若m>n>0，则C是焦点在x轴上的椭圆B．若m=2n（n>0），则C是椭圆，且离心率为C．若mn<0，则C是双曲线，其渐近线方程为D．若m=－2n，则C是双曲线，其离心率为或12．如图，四棱锥P—ABCD的底面为正方形，PD⊥底面ABCD，PD=AD=1，设平面PAD与平面PBC的交线为l，Q为l上的点，下列说法正确的为 A．l//AD B．l⊥平面PDCC．四棱锥Q—ABD的体积随Q点的移动而改变D．直线PB与平面QCD所成角的正弦值的最大值为三、填空题（本题共4小题，每小题5分，共20分）13．复数i(1+i)的实部为___________．14．已知双曲线的左焦点是（－2，0），则a的值为___________．15．斜率为的直线过抛物线C：的焦点，且与C交于A、B两点，则|AB|=_____．16．已知，则tanx=______________．四、解答题（本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤）17．（10分）已知二次方程有一正根和一负根，求实数m的取值范围。 18．（12分）在△ABC中，有，（1）求角C的大小；（2）若a=b=3，求△ABC的面积。 19．（12分）如图，设边长为2的正方形ABCD的中心为O，过点O作平面ABCD的垂线VO，VO=2，E为VO的中点，求与夹角的余弦值。 20．（12分）求直线被圆截得的弦长。 21．（12分）如图，在长方体ABCD—A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．（1）证明：D1E⊥A1D；（2）当E为AB的中点时，求点E到平面ACD1的距离， 22．（12分）已知椭圆C：的离心率为，且过点A（2，1）.（1）求C的方程；（2）点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足，证明：存在定点Q，使得|DQ|为定值。
2022年下学期期中考试试卷高二数学参考答案及评分标准一、单选题1—5 CDCCB 6—8 CAD二、多选题9、AC 10、AD 11、ACD 12、ABD三、填空题13、－1 14、1 15、 16、2四、解答题17、 18、（1）60° （2）19、20、221、以D为坐标原点，DA、DC、DD1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，设AE=x，则A1（1，0，1），D1（0，0，1），E（1，0，0），C（0，2，0），则（2分）（1）证明：因为，所以.所以.（4分）（2）因为E为AB的中点，所以E（1，1，0），则，=（－1，2，0），=（－1，0，1）.（6分）设平面ACD1的法向量为n=(a, b, c)，则即得取c=2，则n=（2，1，2）. （9分）所以点E到平面ACD1的距离