2022-2023学年江苏省盐城市盐都区八年级（上）期中数学试卷（含解析）

这是一份2022-2023学年江苏省盐城市盐都区八年级（上）期中数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本题共8小题，共24分）
下列图案中，是轴对称图形的是( )
A. B.
C. D.
下列各组数中，是勾股数的是( )
A. 0.3，0.4，0.5B. 3，4，7
C. 5，12，13D. 8，15，16
三角形的三边长为(b+c)2=a2+2bc，则这个三角形是( )
A. 等边三角形B. 钝角三角形C. 直角三角形D. 锐角三角形
工人常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使CM=CN，过角尺顶点C作射线OC，由此作法便可得△NOC≌△MOC，其依据是( )
A. SSS
B. SAS
C. ASA
D. AAS
等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边为( )
A. 7cmB. 3cmC. 7cm或3cmD. 8cm
如图，A，B，C表示三个居民小区，为丰富居民们的文化生活，现准备建一个文化广场，使它到三个小区的距离相等，则文化广场应建在( )
A. AC，BC两边高线的交点处B. AC，BC两边中线的交点处
C. AC，BC两边垂直平分线的交点处D. ∠A，∠B两内角平分线的交点处
下列说法正确的是( )
A. 9的平方根3B. 16=±4
C. -9没有立方根D. 平方根等于本身的数只有0
如图，在3×3的网格中，每个网格线的交点称为格点．已知图中A、B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有( )
A. 4个B. 6个C. 8个D. 10个
二、填空题（本题共8小题，共24分）
-27的立方根是______．
等腰三角形的一个内角为100°，则它的底角为______．
已知x，y满足|x+1|+y-2=0，则x+y=______．
如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若BC=12，则△AEF的周长为______．
若一个正数的两个平方根分别为m+1与3m-1，则m=______．
观察下列勾股数组：①3，4，5；②5，12，13；③7，24，25；④9，40，41；….若a，144，145是其中的一组勾股数，则根据你发现的规律，a=______.(提示：5=32+12，13=52+12，…)
如图，在四边形ABCD中，∠ACD=∠BAD=90°，AB=AD，CD=4，AC=12，四边形ABCD的面积为______．
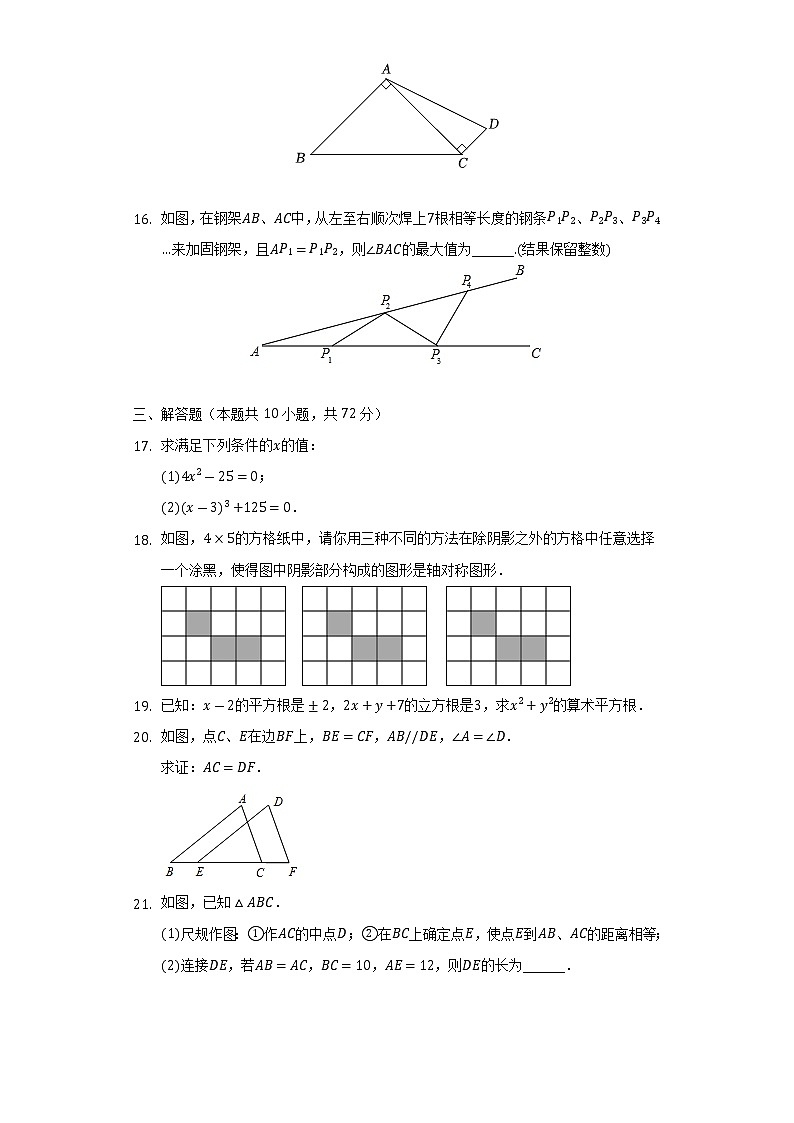
如图，在钢架AB、AC中，从左至右顺次焊上7根相等长度的钢条P1P2、P2P3、P3P4…来加固钢架，且AP1=P1P2，则∠BAC的最大值为______.(结果保留整数)
三、解答题（本题共10小题，共72分）
求满足下列条件的x的值：
(1)4x2-25=0；
(2)(x-3)3+125=0．
如图，4×5的方格纸中，请你用三种不同的方法在除阴影之外的方格中任意选择一个涂黑，使得图中阴影部分构成的图形是轴对称图形．
已知：x-2的平方根是±2，2x+y+7的立方根是3，求x2+y2的算术平方根．
如图，点C、E在边BF上，BE=CF，AB//DE，∠A=∠D．
求证：AC=DF．
如图，已知△ABC．
(1)尺规作图：①作AC的中点D；②在BC上确定点E，使点E到AB、AC的距离相等；
(2)连接DE，若AB=AC，BC=10，AE=12，则DE的长为______．
一架长2.5米的梯子AB如图所示斜靠在一面墙上，这时梯足B离墙底C(∠C=90°)的距离BC为0.7米．
(1)求此时梯顶A距地面的高度AC；
(2)如果梯顶A下滑0.9米，那么梯足B在水平方向，向右滑动了多少米？
如图所示，四边形ABCD中，∠A=90°，AB=AD=4，CD=2，BC=6.求∠ADC的度数．
有一块直角三角形的绿地，量得两直角边长分别为5m，12m.现在要将绿地扩充成等腰三角形绿地，且扩允部分是以12m为直角边的直角三角形，求扩充部分三角形绿地的面积．(如图备用)
定义：点P是△ABC所在平面内任意一点(不与A、B、C重合)，若点P与A、B、C中的某两点的连线夹角是直角，则称点P是△ABC的一个直角点．
(1)如图1，点P是△ABC内一点，满足∠A=60°，∠ABP=10°，∠ACP=20°，试说明点P是△ABC的一个直角点；
(2)如图2，△ABC的顶点都在格点上，AB=AC，D是BC的中点，点P是直线AD上△ABC的直角点，请在图中标出所有符合条件的点P；
(3)如图3，在△ABC中，∠ACB=90°，AC=6，BC=8，点D是AB的中点，点P是射线CD上△ABC的直角点，求CP的长．
【材料阅读】
材料1：我们知道，等边三角形的三边相等．那么等腰直角三角形的三边有何特殊关系呢？我们可以作如下探讨：如图1，在△ABC中，∠ACB=90°，AC=BC，此时我们称△ABC是等腰直角三角形．如果设AC=BC=a，那么由勾股定理得：AB2=a2+a2=2a2，所以AB=2a2=2a.因此，我们得出结论：等腰直角三角形的斜边长等于直角边的2倍．
材料2：如图2，点P是等边△ABC外一点，且满足∠BPC=60°，连接PA，PB，PC，线段PA、PB、PC之间有何等量关系呢？经过探究，小聪同学给出了他的正确思路：
如图3，在PC上截取CQ=PB，连接AQ.因为△ABC是等边三角形，所以AB=AC，∠BAC=60°，由AB=AC，PB=CQ，可证得△ABP≌△ACQ，所以AP=AQ，∠BAP=∠CAQ，故∠PAQ=∠BAC=60°.由可知△APQ是等边三角形，所以PQ=PA.因此最终得出线段PA、PB、PC之间的等量关系是______．
【材料理解】
请结合对材料2的阅读理解，完善以上证明思路．
【材料运用】
请运用上述材料的结论和方法，解决下列问题：如图4，点P是等腰直角三角形ABC外一点(其中∠BAC=90°，AB=AC)，且满足∠BPC=90°，连接PA，PB，PC，试判断线段PA、PB、PC之间的等量关系，并证明你的结论．
【解决问题】
如图5所示，将一只等腰直角三角尺的直角顶点C放置在直线l上并固定，点D是直线l上的一动点，连接AD，BD，已知当AD与BD之和最小时，AD=m，CD=n，则此时BD的长为______.(用含m，n的代数式表示)
答案和解析
1.【答案】A
【解析】解：B，C，D选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
A选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：A．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】C
【解析】解：A、0.3，0.4，0.5，都不是正整数，不是勾股数，故选项不符合题意；
B、32+42≠72，不能构成直角三角形，不是勾股数，故选项不符合题意；
C、52+122=132，能构成直角三角形，都是整数，是勾股数，故选项符合题意；
D、38+152≠162，故不是勾股数，故选项不符合题意．
故选：C．
欲判断是否为勾股数，必须根据勾股数是正整数，同时还需验证两小边的平方和是否等于最长边的平方．
此题主要考查了勾股数，关键是掌握勾股数的定义，及勾股定理的逆定理：已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．
3.【答案】C
【解析】解：因为三角形的三边长为(b+c)2=a2+2bc，
可得：b2+c2=a2，
所以这个三角形是直角三角形，
故选：C．
展开等式后，利用勾股定理的逆定理解答即可．
此题考查了勾股定理的逆定理的应用，熟练掌握因式分解的方法是解本题的关键．
4.【答案】A
【解析】解：由作得OM=ON，CM=CN，
∵OC=OC，
∴△NOC≌△MOC(SSS)．
故选：A．
利用作法得到OM=ON，CM=CN，加上OC为公共边，则根据“SSS”可判断△NOC≌△MOC．
本题考查了作图-复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．
5.【答案】B
【解析】
【分析】
本题考查等腰三角形的性质，三角形的三边关系，涉及分类讨论的思想方法．
已知的边可能是腰，也可能是底边，应分两种情况进行讨论．
【解答】
解：当腰长是3cm时，则另两边是3cm，7cm.而3+390°，则11.25°