第24章 解直角三角形真题训练卷 - 九年级数学上册单元复习辅导突破（华师大版）

这是一份第24章 解直角三角形真题训练卷 - 九年级数学上册单元复习辅导突破（华师大版），文件包含第24章解直角三角形真题训练卷原卷版doc、第24章解直角三角形真题训练卷解析版doc等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
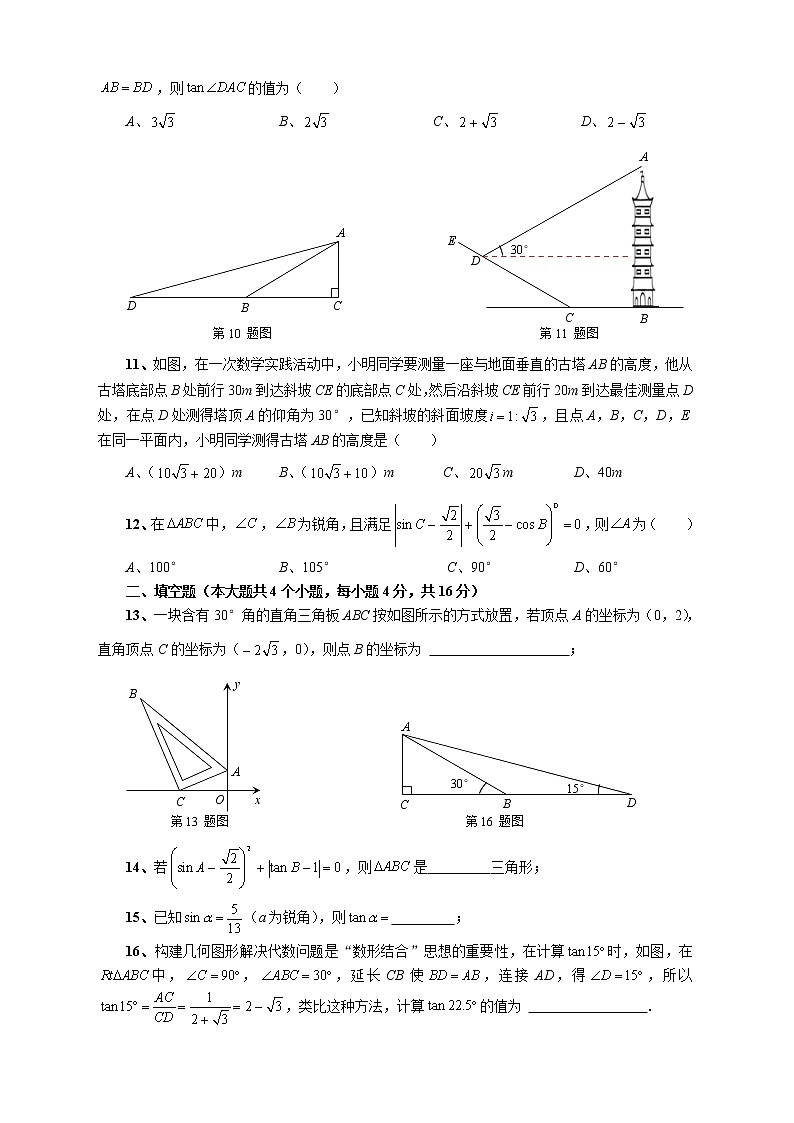
华东师大版九年级上册第24章《解直角三角形》真题训练卷一、选择题（本大题共12个小题，每小题4分，共48分.以下每小题都给出了A、B、C、D四个选项，其中只有一个是符合题目要求的。）1、在中，若各边长都扩大为原来的3倍，则锐角A的正切值（　　）A、扩大为原来的3倍 B、缩小为原来的 C、不变 D、以上都不对2、如图，在中，，，，D是AC的中点，则BD的长为（　　）A、5.5cm B、5cm C、6cm D、6.5cm3、已知中，，，则的值为（　　）A、 B、 C、 D、4、在中，，，，则AB的值为（　　）A、8 B、9 C、10 D、125、已知在中，，若，则等于（　 　）A、 B、 C、 D、16、在中，，则的形状是（　　）A、锐角三角形 B、直角三角形 C、钝角三角形     D、不确定7、如图，在6×6的正方形网格中，的顶点都在小正方形的顶点上，则的值是（　　）A、 B、 C、 D、8、如图，在中，直线MN垂直平分AB交AB于M，交BC于N，且，，则BC的长为（　　）A、6 B、 C、 D、99、等腰三角形底边与底边上的高的比是，则它的顶角为（　　）A、30° B、45° C、60° D、120°10、如图，在中，，，点D是CB延长线上的一点，且，则的值为（　　）A、 B、 C、 D、11、如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔AB的高度，他从古塔底部点B处前行30m到达斜坡CE的底部点C处，然后沿斜坡CE前行20m到达最佳测量点D处，在点D处测得塔顶A的仰角为30°，已知斜坡的斜面坡度，且点A，B，C，D，E在同一平面内，小明同学测得古塔AB的高度是（　　）A、（）m B、（）m       C、m         D、40m12、在中，，为锐角，且满足，则为（　　）A、100° B、105° C、90° D、60°二、填空题（本大题共4个小题，每小题4分，共16分）13、一块含有30°角的直角三角板ABC按如图所示的方式放置，若顶点A的坐标为（0，2），直角顶点C的坐标为（，0），则点B的坐标为 　                　；14、若，则是　     　三角形；15、已知（a为锐角），则　     　；16、构建几何图形解决代数问题是“数形结合”思想的重要性，在计算时，如图，在中，，，延长CB使，连接AD，得，所以，类比这种方法，计算的值为 　             　.三、解答题（本大题6个小题，共56分。解答应写出必要的文字说明或演算步骤。）17、（本小题满分8分）计算：（1）      （2）   18、（本小题满分8分）如图，一艘轮船位于灯塔B的正西方向上的A处，且灯塔B到A处的距离为40海里，轮船沿东北方向匀速航行，速度为20海里/时。（1）多长时间后，轮船行驶到达位于灯塔B的西北方向上的C处？（结果保留根号）（2）若轮船不改变方向行驶，当轮船行驶到达位于灯塔B的北偏东15°方向上的D处时，求灯塔B到D处的距离。（结果保留根号）        19、（本小题满分8分）如图，在中，，，（1）求AB的长；（2）如果CD为边AB上的中线，求的正切值。    20、（本小题满分8分）某校航天爱好者的同学们构建数学模型，使用卷尺和测角仪测量天和核心舱的高度、如图所示，核心舱架设在1米的稳固支架上，他们先在水平地面点B处测得天和核心舱最高点A的仰角为22°，然后沿水平MN方向前进24米，到达点C处，测得点A的仰角为45°，测角仪MB的高度为1.6米，求天和核心舱的高度。（结果精确到0.1米，参考数据：，，，）      21、（本小题满分10分）如图，山区某教学楼后面紧邻着一个土坡，坡面BC平行于地面AD，斜坡AB的坡比为，且米。（1）求坡顶与地面的距离BE的长；（2）为了防止山体滑坡，保障安全，学校决定对该土坡进行改造、经地质人员勘测，当坡角不超过53°时，可确保山体不滑坡、学校计划将斜坡AB改造成AF（如图所示），那么BF至少是多少米？（结果精确到1米）（参考数据：，，）            22、（本小题满分12分）如图，在中，AD是中线，，（1）求的值；（2）求的度数。