广东省汕头市潮南区2022年八年级上学期期末数学试题及答案

这是一份广东省汕头市潮南区2022年八年级上学期期末数学试题及答案，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
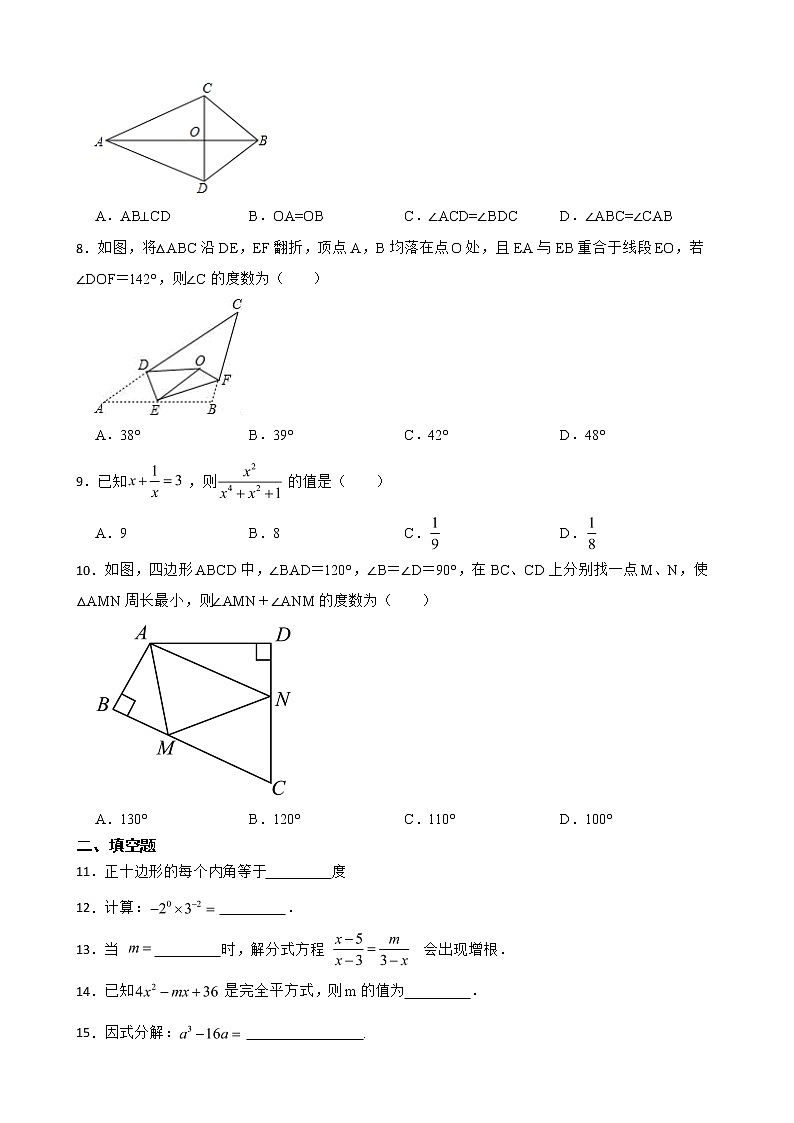
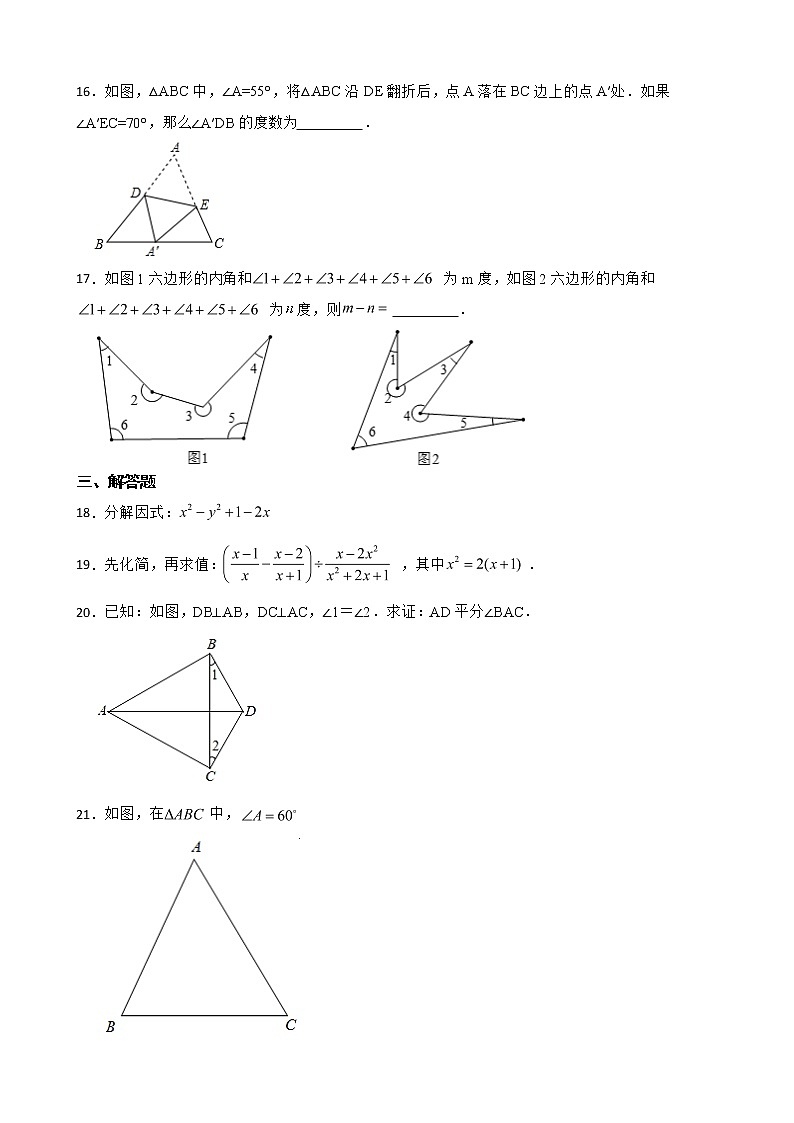
 八年级上学期期末数学试题一、单选题1．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）A． B． C． D．2．已知两条线段a=2cm，b=3.5cm，下列线段中能和a，b构成三角形的是（　　）A．5.5cm B．3.5cm C．1.3cm D．1.5cm3．华为 手机搭载了全球首款7纳米制程芯片，7纳米就是0.000000007米.数据0.000000007用科学记数法表示为(　　).   A． B． C． D．4．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（　　）A．甲和乙 B．乙和丙 C．甲和丙 D．只有丙5．式子 有意义，则实数a的取值范围是（　　）  A．a≥﹣1 B．a≠2C．a≥﹣1且a≠2 D．a＞26．如图，△ABC的三边AB，BC，CA长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于（　　）  A．1：1：1 B．1：2：3 C．2：3：4 D．3：4：57．如图，AC=AD，BC=BD，则下列结果正确的是（　　）A．AB⊥CD B．OA=OB C．∠ACD=∠BDC D．∠ABC=∠CAB8．如图，将△ABC沿DE，EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠DOF＝142°，则∠C的度数为（　　）  A．38° B．39° C．42° D．48°9．已知，则的值是（　　）A．9 B．8 C． D．10．如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，使△AMN周长最小，则∠AMN＋∠ANM的度数为（　　）A．130° B．120° C．110° D．100°二、填空题11．正十边形的每个内角等于　     　度   12．计算：　     　．13．当 　     　时，解分式方程 会出现增根．14．已知是完全平方式，则m的值为　     　．15．因式分解：　            　.16．如图，△ABC中，∠A=55°，将△ABC沿DE翻折后，点A落在BC边上的点A′处．如果∠A′EC=70°，那么∠A′DB的度数为　     　．17．如图1六边形的内角和为m度，如图2六边形的内角和为度，则　     　．三、解答题18．分解因式：19．先化简，再求值：，其中．20．已知：如图，DB⊥AB，DC⊥AC，∠1＝∠2．求证：AD平分∠BAC．21．如图，在中，（ 1 ）尺规作图：作的平分线；（ 2 ）尺规作图：作线段的垂直平分线；（不写作法，保留作图痕迹）（ 3 ）若与交于点，∠ACP=24°，求的度数.22．如图，已知：E是的平分线上一点，，，C、D是垂足，连接，且交于点F．（1）求证：垂直平分．（2）若，请你探究，之间有什么数量关系？并证明你的结论．23．水果店第一次用500元购进某种水果，由于销售状况良好，该店又用1650元购进该品种水果，所购数量是第一次购进数量的3倍，但进货价每千克多了0.5元．（1）第一次所购水果的进货价是每千克多少元？（2）水果店以每千克8元销售这些水果，在销售中，第一次购进的水果有5%的损耗，第二次购进的水果有2%的损耗．该水果店售完这些水果可获利多少元？24．如图，在△ABC和△ADE中，AB＝AD，AC＝AE，∠BAD＝∠CAE，DE分别交BC，AC于点F，G，连接AF．（1）求证：∠C＝∠E；（2）若∠CAE＝24°，求∠AFB的度数．25．如图，等边△ABC中，点D为AB边上的一动点（D不与A、B重合）．过点D作DE∥BC交AC于点E．把△ADE沿直线DE折叠，点A的对应点为P．（1）求证：△ADE为等边三角形；   （2）连接AP，点D在运动过程中线段AP与线段DE是否存在一定的位置关系？证明你的结论；   （3）若等边△ABC的边长为3，当△BDP为直角三角形时，求 的值．  
答案解析部分1．【答案】A2．【答案】B3．【答案】D4．【答案】B5．【答案】C6．【答案】C7．【答案】A8．【答案】A9．【答案】D10．【答案】B11．【答案】14412．【答案】-13．【答案】214．【答案】±2415．【答案】16．【答案】40°17．【答案】018．【答案】解：19．【答案】解：原式===-∵x2=2(x+1)，∴原式=-=-．20．【答案】证明：∵DB⊥AB，DC⊥AC∴∠ABD＝∠ACD＝90°．∵∠1＝∠2，∴DB＝DC，∵AD＝AD，∴Rt△ABD≌Rt△ACD．∴∠BAD＝∠CAD，∴AD平分∠BAC．21．【答案】解：⑴如图，l1为所作；⑵如图，l2为所作；⑶设∠ABP的度数为x∵平分∴=x又∵垂直平分∴∴∴=x又∵又∵，∴即22．【答案】（1）证明：∵E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，∴ED=EC，在Rt△ODE和Rt△OCE中，，∴Rt△ODE≌Rt△OCE（HL），∴OD=OC；∴点O、点E在线段CD的垂直平分线上，∴OE是CD的垂直平分线；（2）解：OE=4EF，证明：∵OE是∠AOB的平分线，∠AOB=60°，∴∠AOE=∠BOE=30°，∵EC⊥OB，ED⊥OA，∴OE=2DE，∠ODF=∠OED=60°，∴∠EDF=30°，∴DE=2EF，∴OE=4EF，23．【答案】（1）解：设第一次所购水果的进货价是每千克x元，依题意，得 =，解得，x=5，经检查，x=5是原方程的解．答：第一次进货价为5元；（2）解：第一次购进：500÷5=100千克，第二次购进：3×100=300千克，获利：[100×（1-5%）×8-500]+[300×（1-2%）×8-1650]=962元．答：第一次所购水果的进货价是每千克5元，该水果店售完这些水果可获利962元．24．【答案】（1）证明：，，即，在和中，，，；（2）解：，，即，，，如图，分别过点A作于点M，过点于点N，在和中，，，，是的角平分线，．25．【答案】（1）证明：∵△ABC为等边三角形，∴∠BAC=∠C=∠ABC=60°  又∵DE∥BC，∴∠ADE=∠ABC=60°，∠AED=∠C=60°， ∴∠ADE=∠AED=∠BAC=60° ，∴△ADE为等边三角形．（2）解：点D在运动过程中线段AP与线段DE互相垂直平分  证明：∵△ADE与△PDE关于直线DE成轴对称，∴DE垂直平分AP，∵△ADE为等边三角形，AP⊥DE,∴AP平分DE,∴ AP、DE互相垂直平分（3）解：由于∠BDP=60°，所以，分∠BPD=90°或∠DBP=90°两种情况  ① 当∠BPD=90°时，∵∠BDP=60°,∴∠PBD=30°,∴ ．∵AD=PD, ∴   即 ②当∠DBP=90°时，同理可得 即， 综上所述，当△BDP是直角三角形时，当 或 ．