期末测试卷03-【对点变式题】最新八年级数学下学期期中期末必考题精准练（人教版）

这是一份期末测试卷03-【对点变式题】最新八年级数学下学期期中期末必考题精准练（人教版），文件包含期末测试卷03-对点变式题最新八年级数学下学期期中期末必考题精准练人教版解析版docx、期末测试卷03-对点变式题最新八年级数学下学期期中期末必考题精准练人教版原卷版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

2021-2022学年八年级下学期数学
期末测试卷03
（考试时间120分钟 满分120分）
注意事项：
1.考生答题前，请将自己的学校、姓名、准考证号请填写在试题卷和答题卡指定位置上，同时认真阅读答题卡上的注意事项.
2.考生答题时，请按题号顺序在答题卡上各题目的答题区域内作答，写在试卷上无效.

第Ⅰ卷（选择题 共24分）
一． 选择题（下列各题的备选答案中，有且仅有一个答案是正确的，每小题3分，共24分）
1．（2022•济宁一模）下列各式是最简二次根式的是（　　）
A．13 B．12 C．a2 D．53
【考点】最简二次根式；
【分析】根据最简二次根式的概念判断即可．
【解答】解：A、13是最简二次根式；
B、12=4×3=23，不是最简二次根式；
C、a2=|a|，不是最简二次根式；
D、53，被开方数的分母中含有字母，不是最简二次根式；
故选：A．
2．（2021春•南平期末）已知四个三角形分别满足下列条件：
①一个内角等于另外两个内角之和； ②三个内角之比为3：4：5；③三边长分别为7，24，25； ④三边之比为5：12：13．其中能判定是直角三角形的有（　　）
A．1个 B．2个 C．3个 D．4个
【考点】勾股定理的逆定理；三角形内角和定理；
【分析】根据三角形的内角和定理或勾股定理的逆定理即可进行判断，从而得到答案．
【解答】解：①设两个较小的角为x，则2x+2x＝180°，则三角分别为45°，45°，90°，故是直角三角形；
②设较小的角为3x，则其于两角为4x，5x，则三个角分别为45°，60°，75°，故不是直角三角形；
③因为三边符合勾股定理的逆定理，故是直角三角形；
④因为52+122＝132符合勾股定理的逆定理，故是直角三角形．
所以有三个直角三角形，故选：C．
3．（2021秋•兰州期末）甲、乙、丙、丁四人进行100m短跑训练，统计近期10次测试的平均成绩都是13.2s，10次测试成绩的方差如下表则这四人中发挥最稳定的是（　　）
选手
甲
乙
丙
丁
方差（s2）
0.020
0.019
0.021
0.022
A．甲 B．乙 C．丙 D．丁
【考点】方差；算术平均数；
【分析】方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
【解答】解：∵s2丁＞s2丙＞s2甲＞s2乙，
方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
∴乙最稳定．
故选：B．
4．（2022春•连城县期中）下列各式计算正确的是（　　）
A．53-23=3 B．65+56=1111 C．35×53=1515 D．82÷22=42
【考点】二次根式的混合运算；
【分析】直接利用二次根式的加减运算法则以及二次根式的乘除运算法则分别化简，进而判断即可．
【解答】解：A.53-23=33，故此选项不合题意；
B.65+56无法合并，故此选项不合题意；
C.35×53=1515，故此选项符合题意；
D.82÷22=4，故此选项不合题意．
故选：C．
5． （2022春•青浦区校级期中）下列命题是真命题的是（　　）
A.有一组对边平行，另一组对边相等的四边形是平行四边形
B．两条对角线相等的四边形是矩形
C．一条对角线平分一组对角的四边形是菱形
D．对角线互相垂直平分的四边形是菱形
【考点】菱形的判定．
【分析】利用平行四边形、矩形、菱形及正方形的判定方法分别判断，即可确定正确的选项．
【解答】解：A、有一组对边平行且相等的四边形是平行四边形，是假命题；
B、两条对角线平分且相等的四边形是矩形，是假命题；
C、一条对角线平分一组对角的平行四边形是菱形，是假命题；
D、对角线互相垂直平分的四边形是菱形，是真命题；
故选：D．
6．（2021秋•阳山县期末）若直线y＝kx+b经过第一、二、四象限，则函数y＝bx﹣k的大致图象是（　　）
A． B． C． D．
【考点】一次函数的性质；一次函数的图象；
【分析】根据一次函数y＝kx+b的图象经过第一、二、四象限，可以得到k和b的正负，然后根据一次函数的性质，即可得到一次函数y＝bx﹣k图象经过哪几个象限，从而可以解答本题．
【解答】解：∵一次函数y＝kx+b的图象经过第一、二、四象限，
∴k＜0，b＞0，
∴b＞0，﹣k＞0，
∴一次函数y＝bx﹣k图象第一、二、三象限，
故选：B．
7.（2022春•禹州市期中）如图点O为数轴的原点，点A和B分别对应的实数是﹣1和1．过点B作
BC⊥AB，以点B为圆心，OB长为半径画弧，交BC于点D；以点A为圆心，AD长为半径画弧，交数轴的正半轴于点E，则点E对应的实数是（　　）

A．5-1 B．5 C．3 D．3-1
【考点】勾股定理；实数与数轴；
【分析】根据勾股定理求出AD，进而得到OE的长，根据实数与数轴的对应关系解答即可．
【解答】解：由题意得，BD＝OB＝1，
在Rt△ABD中，AD=AB2+BD2=22+12=5，
∴OE＝AE﹣1=5-1，
∴点E对应的实数是5-1，
故选：A．
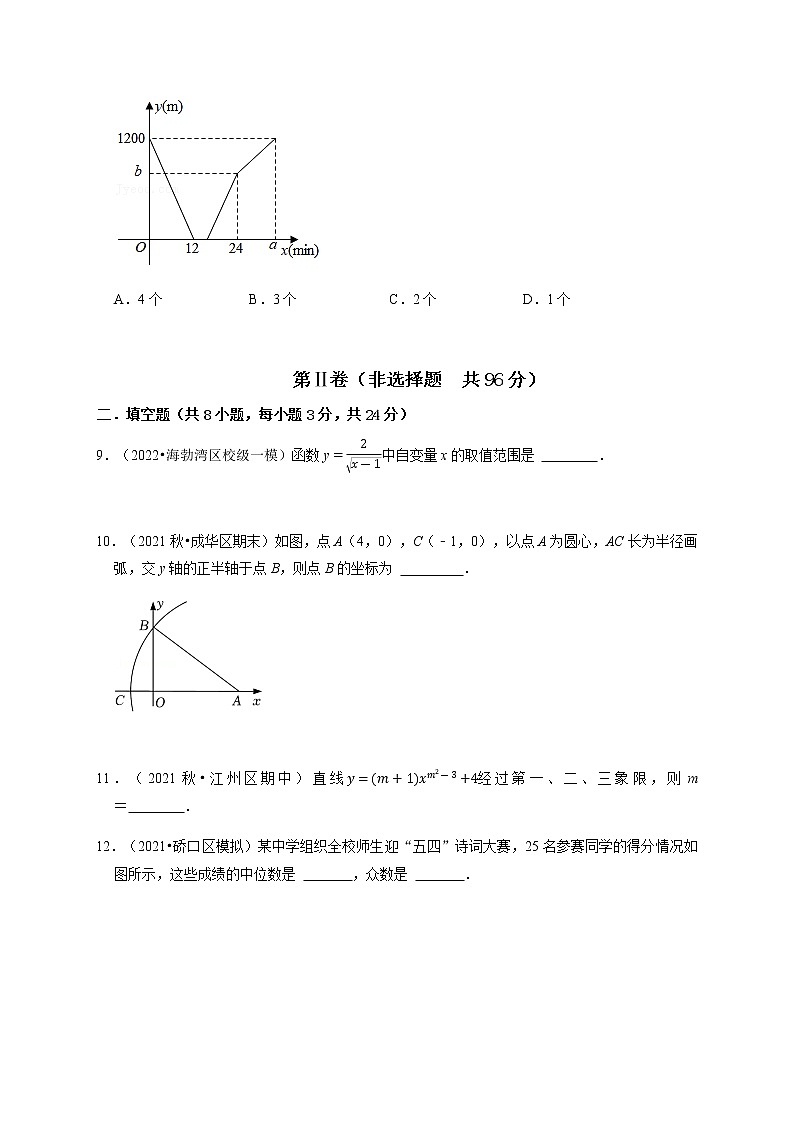
8．（2021秋•福田区校级期末）甲、乙两人分别从A、B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地，甲、乙两人之间的距离y（m）与甲所用时间x（min）之间的函数关系如图所示，给出下列结论：①A，B之间的距离为1200m；②乙行走的速度是甲的1.5倍；③b＝800；④a＝34，其中正确的结论个数为（　　）

A．4个 B．3个 C．2个 D．1个
【考点】一次函数的应用；
【分析】根据函数图象中的数据，可以直接看出A，B之间的距离，从而可以判断①；根据已知，可以先计算乙的速度，然后再计算出甲的速度，从而可以判断②；根据图象中的数据和题意，可以求得甲和乙的速度之和，从而可以得到b的值，从而可以判断③；根据③中的结果和图象，可以求得a的值，从而可以判断④．
【解答】解：由图象可得，
A，B之间的距离为1200m，故①正确；
乙的速度为：1200÷（24﹣4）＝60（m/min），
甲的速度为：1200÷12﹣60＝100﹣60＝40（m/min），
60÷40＝1.5，
即乙行走的速度是甲的1.5倍，故②正确；
甲乙的速度之和为：1200÷12＝100（m/min），则b＝（24﹣12﹣4）×100＝800，故③正确；
a＝1200÷40+4＝30+4＝34，故④正确；
故选：A．



第Ⅱ卷（非选择题 共96分）
二． 填空题（共8小题，每小题3分，共24分）
9．（2022•海勃湾区校级一模）函数y=2x-1中自变量x的取值范围是 　 　．
【考点】函数自变量的取值范围；
【分析】根据二次根式的被开方数是非负数、分母不为0列出不等式，解不等式得到答案．
【解答】解：由题意得：x﹣1＞0，
解得：x＞1，
故答案为：x＞1．
10．（2021秋•成华区期末）如图，点A（4，0），C（﹣1，0），以点A为圆心，AC长为半径画弧，交y轴的正半轴于点B，则点B的坐标为 　 　．

【考点】勾股定理；坐标与图形性质；
【分析】根据已知可得AB＝AC＝5，OA＝4．利用勾股定理即可求解．
【解答】解：根据已知可得：AB＝AC＝5，OA＝4．
在Rt△ABO中，OB=AB2-OA2=3．
∴B（0，3）．
故答案为：（0，3）．

11．（2021秋•江州区期中）直线y=(m+1)xm2-3+4经过第一、二、三象限，则m＝　 　．
【考点】一次函数的定义；
【分析】根据一次函数的定义和性质得出m2﹣3＝1且m+1＞0，再求出m即可．
【解答】解：∵直线y=(m+1)xm2-3+4经过第一、二、三象限，
∴m2﹣3＝1且m+1＞0，
解得：m＝2，
故答案为：2．
12．（2021•硚口区模拟）某中学组织全校师生迎“五四”诗词大赛，25名参赛同学的得分情况如图所示，这些成绩的中位数是 　　 ，众数是 　 　．

【考点】众数；中位数；
【分析】利用中位数和众数的定义求解．
【解答】解：共有25个数，最中间的数为第13数，是96，所以数据的中位数为96分；
98出现了9次，出现次数最多，所以数据的众数为98分．
故答案为：96分，98分．
13．（2021秋•重庆期中）某音像社对外出租的光盘的收费方法是：每张光盘出租后的头两天，每天收0.8元，以后每天收0.5元，那么一张光盘在出租后n天（n≥2）应收租金　 　元．
【考点】根据实际问题列一次函数关系式；
【分析】先求出出租后的头两天的租金，然后用“n﹣2”求出超出两天的天数，进而求出超出两天后的租金，然后用“头两天的租金+超出两天后的租金”解答即可．
【解答】解：当租了n天（n≥2），则应收钱数：
0.8×2+（n﹣2）×0.5，
＝1.6+0.5n﹣1，
＝0.5n+0.6（元）．
答：共收租金（0.5n+0.6）元．
故答案为：（0.5n+0.6）．
14．（2021秋•仓山区校级期末）若1≤x≤4，则：|1﹣x|-(x-4)2化简的结果为 　 　．
【考点】二次根式的性质与化简；
【专题】计算题；二次根式；运算能力．
【分析】先把(x-4)2=|x﹣4|，根据1≤x≤4，利用绝对值的性质进行化简，然后计算．
【解答】解：∵1≤x≤4，
∴|1﹣x|-(x-4)2
＝|1﹣x|﹣|x﹣4|
＝x﹣1﹣（4﹣x）
＝x﹣1﹣4+x
＝2x﹣5；
故答案为：2x﹣5．
15．（2020春•麻城市校级期末）若直角三角形的两边长分别为1和2，则斜边上的中线长为　 　．
【考点】直角三角形斜边上的中线；
【分析】分2是斜边、2是直角边两种情况，根据勾股定理和直角三角形的性质解答即可．
【解答】解：当2是斜边时，斜边上的中线长为：2×12=1，
当2是直角边时，斜边长=12+22=5，
∴斜边上的中线长为52，
故答案为：1或52．
16．（2021春•开江县期末）如图，分别以Rt△ABC的直角边AC，斜边AB为边向外作等边△ACD和△ABE，F为AB的中点，连接DF、EF，∠ACB＝90°，∠ABC＝30°．则以下4个结论：①AC⊥DF；②四边形BCDF为平行四边形；③DA+DF＝BE；④S△ACD：S四边形BCDE＝1：7，其中，正确的是　 　．


【考点】平行四边形的判定与性质；全等三角形的判定与性质；等边三角形的性质；含30度角的直角三角形；
【分析】由平行四边形的判定定理判断②，再由平行四边形的性质和平行线的性质判断①，然后由三角形三边关系判断③，最后由等边三角形的性质分别求出△ACD、△ACB、△ABE的面积，计算即可判断④．
【解答】解：∵∠ACB＝90°，∠ABC＝30°，
∴∠BAC＝60°，AC＝AB，
∵△ACD是等边三角形，
∴∠ACD＝60°，
∴∠ACD＝∠BAC，
∴CD∥AB，
∵F为AB的中点，
∴BF＝AB，
∴BF∥AB，CD＝BF，
∴四边形BCDF为平行四边形，故②正确；
∵四边形BCDF为平行四边形，
∴DF∥BC，
又∵∠ACB＝90°，
∴AC⊥DF，故①正确；
∵DA＝CA，DF＝BC，AB＝BE，BC+AC＞AB，
∴DA+DF＞BE，故③错误；
设AC＝x，则AB＝2x，
∴S△ACD＝x2，S△ACB＝x2，S△ABE＝x2，
∴＝＝，故④正确；
故答案为：①②④．







三、 解答题（本大题共9小题，满分共72分）
17．（本题满分8分）（2021秋•碑林区校级期末）计算：
（1）-12-6×13-（2022﹣π）0+|2﹣43|．

（2）6×3+9127-（2+3）（2-3）；

【考点】二次根式的混合运算；平方差公式；零指数幂；负整数指数幂；分母有理化；
【分析】（1）先根据平方差公式计算乘法，再算加减法即可求解；
（2）先算负整数指数幂，二次根式的化简，零指数幂，绝对值，再计算加减法．
【解答】解：
（1）（13）﹣1-12-6×13-（2022﹣π）0+|2﹣43|
＝3﹣23-23-1+43-2
＝0．
（2）6×3+9127-（2+3）（2-3）
＝32+3-（2﹣3）
＝32+3+1；
18．（本题满分7分）（2022春•常州期中）如图，四边形ABCD是平行四边形，AE，CF分别平分∠BAD和∠BCD，交BD于点E，F．
（1）若∠BCF＝65°，求∠ABC的度数；
（2）连接CE，AF，求证：四边形AECF是平行四边形．

【考点】平行四边形的判定与性质；
【分析】（1）由平行四边形的性质可得出答案；
（2）根据ASA证明△ABE≌△CDF，由全等三角形的性质得出AE＝CF，AE∥CF，则可得出结论．
【解答】（1）解：∵CF平分∠BCD，
∴∠BCD＝2∠BCF＝65°×2＝130°，
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ABC＝180°﹣∠BCD＝180°﹣130°＝50°；
（2）证明：∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，∠BAD＝∠DCB，
∴∠ABE＝∠CDF，
∵∠BAE=12∠BAD，∠DCF=12∠DCB，
∴∠BAE＝∠DCF，
∴△ABE≌△CDF（ASA）．
∴∠AEB＝∠CFD，AE＝CF，
∴∠AEF＝∠CFE，
∴AE∥CF，
∴四边形AECF是平行四边形．
19．（本题满分6分）（2021春•开江县期末）先化简再求值：x2-xx2-2x+1÷(3x+1x2-1+xx+1)，其中x=3-1．
【考点】分式的化简求值；
【专题】分式．
【分析】先化简分式，然后将x的值代入求值．
【解答】解：原式=x(x-1)(x-1)2÷[3x+1(x+1)(x-1)+x(x-1)(x+1)(x-1)]
=xx-1÷(x+1)2(x+1)(x-1)
=xx-1⋅x-1x+1
=xx+1，
当x=3-1 时，
原式=3-13=3-33


20．（本题满分7分）（2021秋•门头沟区期末）已知，如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于D，过D作DE∥AC交AB于E．
（1）求证：AE＝DE；
（2）如果AC＝3，AD=23，求AE的长．

【考点】勾股定理；角平分线的性质；等腰三角形的判定与性质；
【分析】（1）根据平行线的性质和角平分线的定义解答即可；
（2）过点D作DF⊥AB于F，根据勾股定理和全等三角形的判定和性质解答即可．
【解答】（1）证明：∵DE∥AC，
∴∠CAD＝∠ADE，
∵AD平分∠BAC，
∴∠CAD＝∠EAD．
∴∠EAD＝∠ADE．
∴AE＝DE；
（2）解：过点D作DF⊥AB于F．

∵∠C＝90°，AC＝3，AD=23，
在Rt△ACD中，由勾股定理得 AC2+DC2＝AD2．
∴DC=3．
∵AD平分∠BAC，
∴DF＝DC=3．
又∵AD＝AD，∠C＝∠AFD＝90°，
∴Rt△DAC≌Rt△DAF（HL）．
∴AF＝AC＝3，
∴Rt△DEF中，由勾股定理得 EF2+DF2＝DE2．
设AE＝x，则DE＝x，EF＝3﹣x，
∴(3-x)2+(3)2=x2，
∴x＝2．
∴AE＝2．
21．（本题满分7分）（2022•红桥区一模）随着移动计算技术和无线网络的快速发展，移动学习方式越来越引起人们的关注．某校计划将这种学习方式应用到教育教学中，从各年级共1500名学生中随机抽取了部分学生，对其家庭中拥有的移动设备情况进行了调查，并绘制出如下的统计图①和图②，根据相关信息，解答下列问题：

（1）本次接受随机抽样调查的学生人数为 　　 图①中m的值为 　 　．
（2）求本次调查获取的样本数据的众数、中位数和平均数；
（3）根据样本数据，估计该校学生家庭中拥有3台移动设备的学生人数．
【考点】众数；用样本估计总体；加权平均数；中位数；
【分析】（1）根据家庭中拥有1台移动设备的人数及所占百分比可得查的学生人数，将拥有4台移动设备的人数除以总人数可得m的值；
（2）根据众数、中位数、加权平均数的定义计算即可；
（3）将样本中拥有3台移动设备的学生人数所占比例乘以总人数1500即可．
【解答】解：（1）本次接受随机抽样调查的学生人数为：48%=50（人），
图①中m的值为1650×100＝32；
（2）∵这组样本数据中，4出现了16次，出现次数最多，
∴这组数据的众数为4；
∵将这组数据从小到大排列，其中处于中间的两个数均为3，有3+32=3，
∴这组数据的中位数是3；
由条形统计图可得x=1×4+2×10+3×14+4×16+5×650=3.2，
∴这组数据的平均数是3.2．
（3）1500×28%＝420（人）．
答：估计该校学生家庭中；拥有3台移动设备的学生人数约为420人．
故答案为：50，32．

22．（本题满分8分）（2022春•如皋市期中）如图，△ABC中，D，E分别为AB，BC的中点，DG⊥AC，EF⊥AC，垂足分别为G，F．
（1）求证：四边形DEFG为矩形；
（2）若AB＝AC＝25，EF＝2，求CF的长．

【考点】矩形的判定与性质；勾股定理；三角形中位线定理；
【分析】（1）欲证明四边形DEFG为矩形，只需推知该四边形为平行四边形，且有一内角为直角即可；
（2）首先根据直角三角形斜边上中线的性质求得AE＝DE=5；然后在直角△AEF中利用勾股定理得到AF的长度；最后结合AB＝AC＝AG+FG+CF＝25求解即可．
【解答】（1）证明：∵点D是AB的中点，E点是BC的中点，
∴DE是△ABC的中位线．
∴DE∥AC．
∵DG⊥AC，EF⊥AC，
∴EF∥DG．
∴四边形DEFG是平行四边形．
又∵∠EFG＝90°，
∴四边形DEFG为矩形；
（2）∵AB＝AC＝25，EF＝2，D点是BC的中点，
∴DE＝AD=12AB=5．
由（1）知，四边形DEFG为矩形，则GF＝DE=5．
在直角△ADG中，EF＝2，AD=5，由勾股定理得：AG=AD2-EF2=(5)2-22=1．
∵AB＝AC＝25，FG＝ED=5，
∴CF＝AC﹣AG﹣GF＝25-1-5=5-1．
23．（本题满分8分）（2022•云南模拟）近年来，四川天府新区取得了飞速的发展，以成都科学城发展为例，兴隆湖畔集结了一大批领先的科技创新领军项目，正如火如荼地推进建设，据报道，新区某公司打算购买A，B两种花装点城区道路，公司负责人到花卉基地调查发现：购买1盆A种花和2盆B种花需要14元，购买2盆A种花和1盆B种花需要13元．
（1）求A，B两种花的单价各为多少元？
（2）公司若购买A，B两种花共10000盆，设购买的A种花m盆（3000≤m≤5000），总费用为W元；
①求W与m的关系式；
②请你帮公司设计一种购花方案，使总花费最少？并求出最少费用为多少元？
【考点】一次函数的应用；二元一次方程组的应用；
【分析】（1）根据购买1盆A种花和2盆B种花需要14元，购买2盆A种花和1盆B种花需要13元，可以列出相应的二元一次方程组，然后即可得到A、B两种花的单价各为多少元；
（2）①根据题意，可以写出W与m的关系式；
②根据①中的函数关系式和一次函数的性质，即可得到使总花费最少的购花方案，并求出最少费用．
【解答】解：（1）设A种花的单价为a元，B种花的单价为b元，
a+2b=142a+b=13，
解得a=4b=5，
即A种花的单价为4元，B种花的单价为5元；
（2）①由题意可得，
W＝4m+5（10000﹣m）＝﹣m+50000，
即W与m的关系式是W＝﹣m+50000（3000≤m≤5000）；
②∵W＝﹣m+50000，
∴W随m的增大而减小，
∵3000≤m≤5000，
∴当m＝5000时，W取得最小值，此时W＝45000，10000﹣m＝5000，
即当购买A种花5000盆、B种花5000盆时，总花费最少，最少费用为45000元．


24．（本题满分10分）（2021春•绵阳期末）如图1，在正方形ABCD中，BC＝9，点E在AD上，AE＝AD，点G在CD上，且DG：GC＝2：7，连接BE，EG．
（1）求证：BE⊥EG；
（2）如图2，延长EG与∠ADC的邻补角∠CDF的平分线交于点P，连接BP交CD于M，连接EM．
①求证：BE＝EP；
②求EM的长．

【考点】四边形综合题；
【分析】（1）由正方形的性质可求AE＝3，DE＝6，DG＝2，GC＝7，利用勾股定理及勾股定理逆定理可得BG2＝BE2+EG2，可得结论；
（2）①由“ASA”可证△BHE≌△EDP，可得BE＝EP；
②由“SAS”可证△AGB≌△CMB，△EBG≌△EBM，可得GE＝EM，在Rt△EMD中，利用勾股定理可求CM的长，即可求解．
【解答】证明：（1）如图1，连接BG，

∵四边形ABCD是正方形，
∴AB＝BC＝CD＝AD＝9，∠A＝∠C＝∠D＝90°，
∵AE＝AD，DG：GC＝2：7，
∴AE＝3，DE＝6，DG＝2，GC＝7，
∴BE2＝AB2+AE2＝9+81＝90，EG2＝DE2+DG2＝36+4＝40，BG2＝BC2+GC2＝81+49＝130，
∴BG2＝BE2+EG2，
∴∠BEG＝90°，
∴BE⊥EG；
（2）①如图2，在AB上截取AH＝AE，连接EH，

∵AH＝AE，AD＝AB，
∴∠AHE＝∠AEH＝45°，ED＝BH，
∴∠EHB＝135°，
∵DP平分∠FDC，
∴∠PDC＝∠PDF＝45°，
∴∠EDP＝135°＝∠EHB，
∵∠AEB+∠ABE＝90°＝∠AEB+∠DEP，
∴∠ABE＝∠DEP，
∴△BHE≌△EDP（ASA），
∴EB＝EP；
②如图3，延长DA至G，使AG＝CM，连接BG，

∵AG＝CM，∠BAG＝∠BCM，AB＝BC，
∴△AGB≌△CMB（SAS），
∴BG＝BM，∠ABG＝∠CBM，
∵BE＝EP，∠BEP＝90°，
∴∠EBP＝45°，
∴∠ABE+∠CBM＝45°，
∴∠ABE+∠ABG＝45°，
∴∠GBE＝45°＝∠EBP，
∴△EBG≌△EBM（SAS），
∴GE＝EM，
∴EM＝CM+3，
∵EM2＝DE2+DM2，
∴（3+CM）2＝（9﹣CM）2+36，
∴CM＝，
∴EM＝+3＝．
25． （本题满分11分）（2021春•柳南区校级期末）如图①，在矩形OACB中，点A、B分别在x轴、y轴正半轴上，点C在第一象限，OA＝8，OB＝6．
（1）请直接写出点C的坐标；
（2）如图②，点F在BC上，连接AF，把△ACF沿着AF折叠，点C刚好与线段AB上一点C'重合，求线段CF的长度；
（3）如图③，动点P（x，y）在第一象限，且y＝2x﹣6，点D在线段AC上，是否存在直角顶点为P的等腰直角△BDP，若存在，请求出点P的坐标；若不存在，请说明理由．

【考点】一次函数综合题；
【分析】（1）由矩形的性质可得BC＝OA＝8，AC＝OB＝6，AC∥OB，BC∥OA，即可求解；
（2）由折叠的性质的可得AC＝AC'＝6，CF＝C'F，∠C＝∠AC'F＝60°，由勾股定理可求CF的长；
（3）分两种情况讨论，利用全等三角形的性质可求PF＝BE，EP＝DF，即可求解．
【解答】解：（1）∵四边形ABCD是矩形，
∴BC＝OA＝8，AC＝OB＝6，AC∥OB，BC∥OA，
∴点C的坐标（8，6）；
（2）∵BC＝8，AC＝6，
∴AB=BC2+AC2=64+36=10，
∵把△ACF沿着AF折叠，点C刚好与线段AB上一点C'重合，
∴AC＝AC'＝6，CF＝C'F，∠C＝∠AC'F＝90°，
∴BC'＝AB﹣AC'＝4，
∵BF2＝C'F2+C'B2，
∴（8﹣CF）2＝CF2+16，
∴CF＝3；
（3）设点P（a，2a﹣6），
当点P在BC下方时，如图③，过点P作EF∥BC，交y轴于E，交AC于F，

∵△BPD是等腰直角三角形，
∴BP＝PD，∠BPD＝90°，
∴EF∥BC，
∴∠BEP＝∠BOA＝90°，∠PFD＝∠CAO＝90°，
∴∠BPE+∠DPF＝∠DPF+∠PDF，
∴∠BPE＝∠PDF，
∴△BPE≌△PDF（AAS），
∴PF＝BE＝6﹣（2a﹣6）＝12﹣2a，EP＝DF，
∵EF＝EP+PF＝a+12﹣2a＝8，
∴a＝4，
∴点P（4，2）；
当点P在BC的上方时，如图④，过点P作EF∥BC，交y轴于E，交AC的延长线于F，

同理可证△BPE≌△PDF，
∴BE＝PF＝2a﹣6﹣6＝2a﹣12，
∵EF＝EP+PF＝a+2a﹣12＝8，
∴a=203，
∴点P（203，223），