浙江省温州市第二中学2022-2023学年八年级上学期期中数学试卷(含答案)

2022-2023学年浙江省温州二中八年级（上）期中数学试卷

一、选择题（本题有10小题，每小题3分，共30分）

1．下列图形中，是轴对称图形的是　　

A． B． 

C． D．

2．如图所示，在数轴上表示不等式正确的是　　

A． B． C． D．

3．若一个三角形的两边长分别是2和4，则第三边长可能是　　

A．1 B．2 C．4 D．6

4．下列条件中，能判定为直角三角形的是　　

A． B． 

C． D．，

5．对于命题“如果，那么”，能说明它是假命题的反例是　　

A． B． C． D．

6．如图，已知，补充下列哪一个条件，仍不能判定和全等的是　　

A． B． C． D．

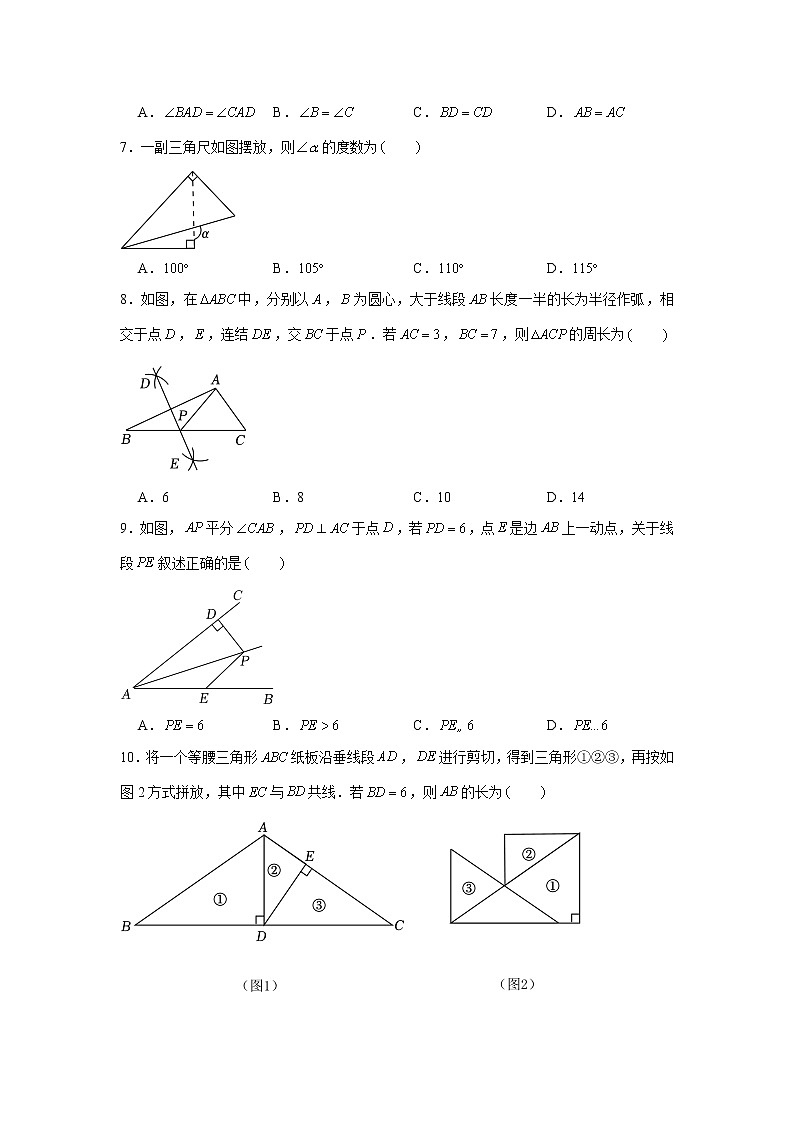
7．一副三角尺如图摆放，则的度数为　　

A． B． C． D．

8．如图，在中，分别以，为圆心，大于线段长度一半的长为半径作弧，相交于点，，连结，交于点．若，，则的周长为　　

A．6 B．8 C．10 D．14

9．如图，平分，于点，若，点是边上一动点，关于线段叙述正确的是　　

A． B． C． D．

10．将一个等腰三角形纸板沿垂线段，进行剪切，得到三角形①②③，再按如图2方式拼放，其中与共线．若，则的长为　　

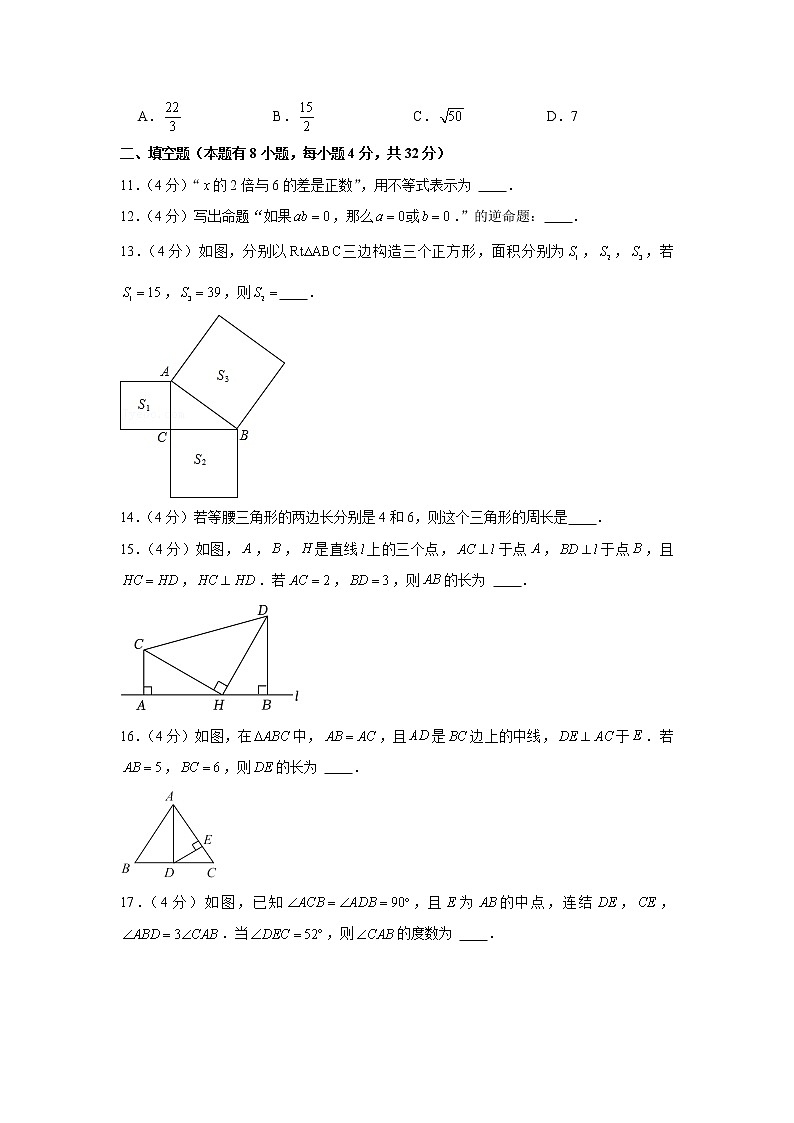
A． B． C． D．7

二、填空题（本题有8小题，每小题4分，共32分）

11．（4分）“的2倍与6的差是正数”，用不等式表示为 　　．

12．（4分）写出命题“如果，那么或．”的逆命题：　　．

13．（4分）如图，分别以三边构造三个正方形，面积分别为，，，若，，则　　．

14．（4分）若等腰三角形的两边长分别是4和6，则这个三角形的周长是　　．

15．（4分）如图，，，是直线上的三个点，于点，于点，且，．若，，则的长为 　　．

16．（4分）如图，在中，，且是边上的中线，于．若，，则的长为 　　．

17．（4分）如图，已知，且为的中点，连结，，．当，则的度数为 　　．

18．（4分）

三、解答题（本题有6小题，共58分）

19．（8分）如图，中，，，与的平分线交于点，过做分别交，于点，．求的周长．请补全以下的解答过程．

解：平分（已知），

（角平分线的定义），

又（已知），

　　　　，

　　，

　　　　．

同理可得：　　．

的周长

　　　　．

20．（6分）当时，

（1）请比较与的大小，并说明理由．

（2）若，则的取值范围为 　　．（直接写出答案）

21．（8分）在下列网格中，每个小正方形的边长均为1．请按要求画出格点三角形．

（1）在图1中画出一个等腰．

（2）在图2中画出一个，且其三边都不与网格线重合．

22．（10分）如图，已知，相交于点，且，．

（1）求证：．

（2）若，求的度数．

23．（12分）等边中，点，分别是边，上的点，且，，交于点．

（1）求证：．

（2）求的度数．

（3）若，，则的面积为 　　．（直接写出答案）

24．（14分）如图1，在长方形中，，，动点从点出发，沿边，向点运动．

（1）当点在边上，且时，求的度数．

（2）当的面积为20时，求的长．

（3）如图2，若，关于直线对称．

①连结，，当点在边上时，求的面积．

②当直线恰好经过点时，请直接写出的长度．

2022-2023学年浙江省温州二中八年级（上）期中数学试卷

参考答案与试题解析

一、选择题（本题有10小题，每小题3分，共30分）

1．【解答】解：，，选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；

选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；

故选：．

2．【解答】解：由题意，得：，

故选：．

3．【解答】解：设第三边的长为，

由题意得：，即，

观察选项，只有选项符合题意．

故选：．

4．【解答】解：．由无法得到为直角三角形，故本选项符合题意；

．，

，无法得到为直角三角形，故本选项符合题意；

．，，

最大角，

是直角三角形，故本选项符合题意；

．，，，，

，

不是直角三角形，故本选项不符合题意．

故选：．

5．【解答】解：当时，满足条件，但不能得出的结论，

能说明命题“如果，那么”是假命题的反例是，

故选：．

6．【解答】解：，

，

，

添加，

，

故选项不符合题意；

添加，

，

故选项不符合题意；

添加，

，

故选项不符合题意；

添加，不能判定，

故选项符合题意，

故选：．

7．【解答】解：如图，

由题意得：，，，

，

．

故选：．

8．【解答】解：由作法得垂直平分，

，

的周长．

故选：．

9．【解答】解：过点作于，如图，

平分，，，

，

点是边上一动点，

．

故选：．

10．【解答】解：如图，设为，为，为，图2中的余角为，

为等腰三角形，，

，，

，

，

结合两图，可得，

设为，

根据勾股定理得，

，

解得：，

，

故选：．

二、填空题（本题有8小题，每小题4分，共32分）

11．【解答】解：“的2倍与6的差是正数”用不等式表示为，

故答案为：．

12．【解答】解：命题“如果，那么或．”的逆命题是如果或，那么，

故答案为：如果或，那么．

13．【解答】解：由勾股定理得：，

，

．

故答案为：24．

14．【解答】解：①若4为腰，满足构成三角形的条件，周长为；

②若6为腰，满足构成三角形的条件，则周长为．

故答案为：14或16．

15．【解答】解：于点，于点，，

，

，

在和中，

，

，

，，

，

的长为5，

故答案为：5．

16．【解答】解：在中，，且是边上的中线，

，，

在中，由勾股定理得，

，

，

，

，

故答案为：．

17．【解答】解：设，

，

，

，且为的中点，

，，

，，

，

，

，

，

，

的度数为．

故答案为：．

18．【解答】解：如图，连接与，

由研究成果可知，

，

，

设的面积为，

则的面积为，

，

，

，

的面积为，

，

，

四边形的面积．

故答案为：3，．

三、解答题（本题有6小题，共58分）

19．【解答】解：平分（已知），

（角平分线的定义），

又（已知），

（两直线平行，内错角相等），

，

（等腰三角形的判定）．

同理可得：．

的周长

．

故答案为：，两直线平行，内错角相等；，，等腰三角形的判定；，，．

20．【解答】解：（1），

理由是：，

，

，

；

（2），，

，

，

即的取值范围是．

故答案为：．

21．【解答】解：（1）根据等腰三角形的定义画出图形即可；

（2）根据直角三角形的定义画出图形即可．

22．【解答】（1）证明：在与中，

，

；

（2），

，

又，

．

23．【解答】（1）证明：为等边三角形，

，，

在和中，

，

；

（2）解：由（1）可知：，

，

；

（3）解：过点作交的延长线于，

，

，

，

由勾股定理得：，

，

故答案为：．

24．【解答】解：（1）四边形为长方形，故，，

当时，

则，

为等腰直角三角形，

；

（2）当点在上时，的面积为长方形面积的一半，即30，

当的面积为20时，点在上，

则的面积，

解得：，

；

（3）①，关于直线对称，

故，而，

则的面积；

②当点在上时，如（图，

在中，，，则，

则，则，

在中，；

当点在上时，如（图，

由题意得：，，，，

在中，，，则，

则，

，则，

，则，

在中，，

则，

综上，的长度为8或．