初中人教版第四章 几何图形初步4.4 课题学习 设计制作长方体形状的包装纸盒精品课件ppt

这是一份初中人教版第四章 几何图形初步4.4 课题学习 设计制作长方体形状的包装纸盒精品课件ppt，共42页。PPT课件主要包含了学习目标，导入新知，合作探究，巩固新知，三棱锥，常见几何体的展开图，四棱锥，长方体，三棱柱，正方体等内容，欢迎下载使用。
1.根据实物图进一步了解长方体的特征，掌握长方体展开图的特点。（重点）2.能独立完成包装纸盒的制作。（难点）3.通过制作过程体会立体图形与平面图形的对应关系。
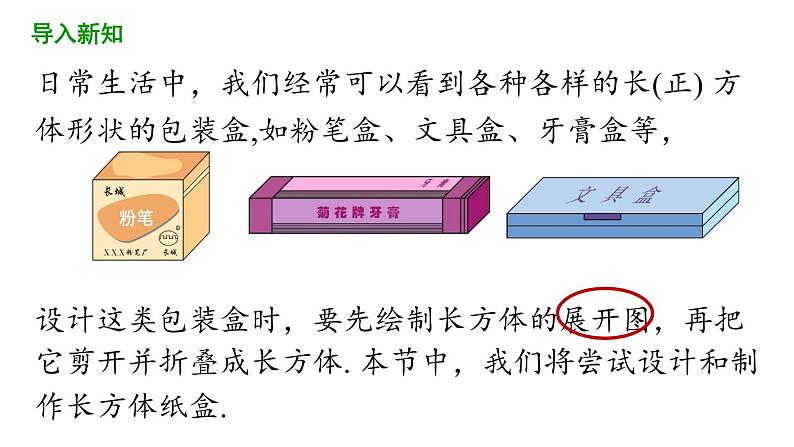
日常生活中，我们经常可以看到各种各样的长(正) 方体形状的包装盒,如粉笔盒、文具盒、牙膏盒等，
设计这类包装盒时，要先绘制长方体的展开图，再把它剪开并折叠成长方体. 本节中，我们将尝试设计和制作长方体纸盒.
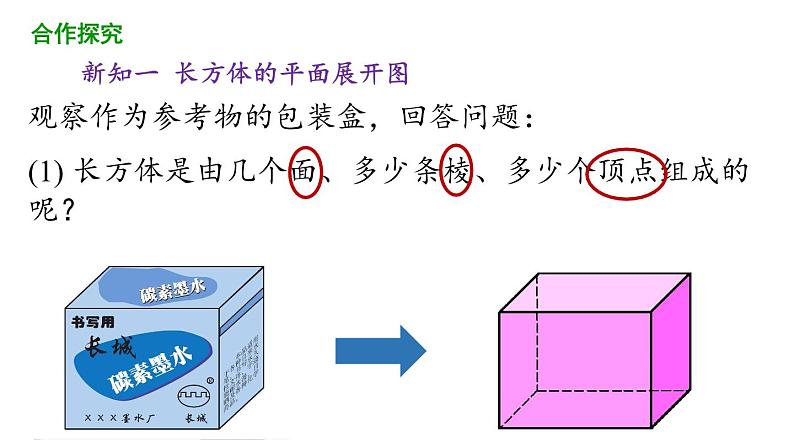
(1) 长方体是由几个面、多少条棱、多少个顶点组成的呢？
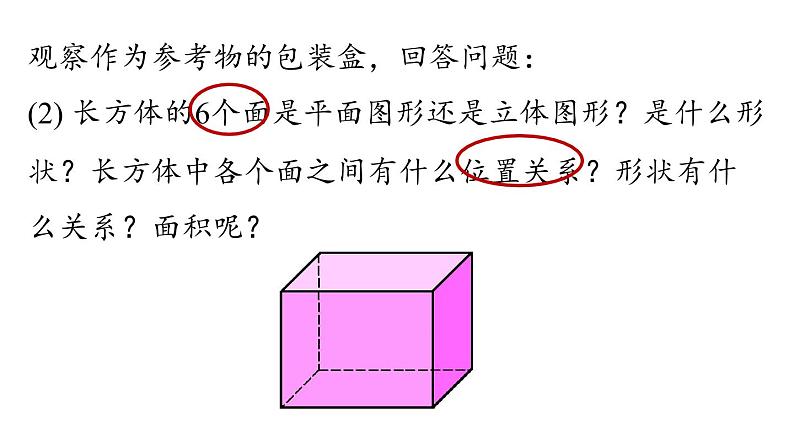
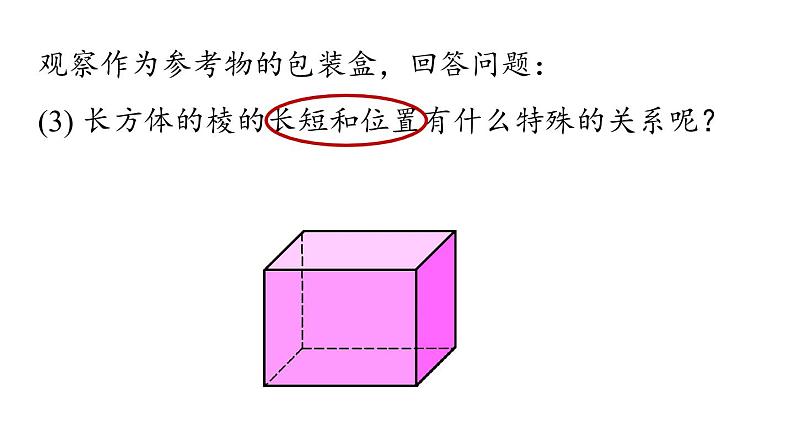
观察作为参考物的包装盒，回答问题：
新知一 长方体的平面展开图
(2) 长方体的6个面是平面图形还是立体图形？是什么形状？长方体中各个面之间有什么位置关系？形状有什么关系？面积呢？
(3) 长方体的棱的长短和位置有什么特殊的关系呢？
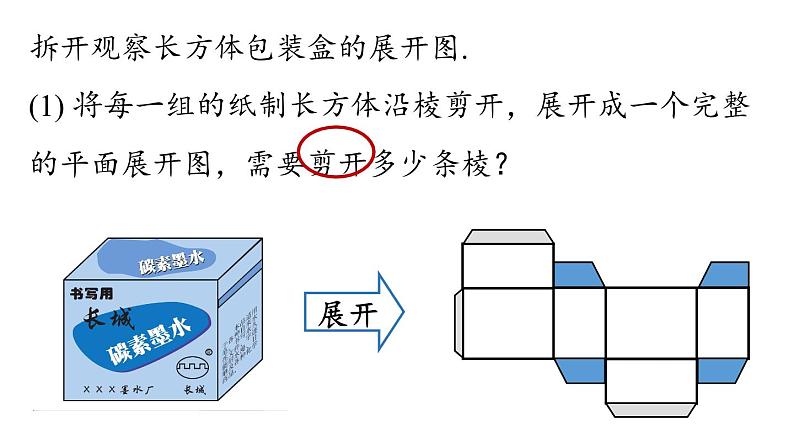
拆开观察长方体包装盒的展开图.
(1) 将每一组的纸制长方体沿棱剪开，展开成一个完整的平面展开图，需要剪开多少条棱？
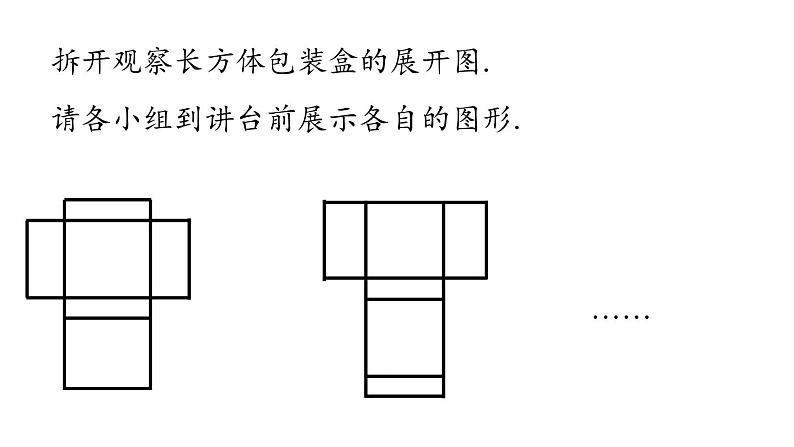
请各小组到讲台前展示各自的图形.
(2) 所得的平面展开图是什么样的？找出对应长方体各面、棱的相应部分，找出其中的关系．
观察它是如何折叠并粘到一起的，重点观察一下它是如何折叠的．
还原表面展开图为包装盒.
例 某种商品的外包装箱是长方体，其展开图的面积为 430 平方分米(如图)，其中 BC=5 分米，EF=10 分米，则 AB 的长度为 分米．
解：由题意得 2×(5AB+10AB+5×10)=430，解得 AB=11．
要得到如图所示的长方体形状的墨水盒，设计方案内容包括：包装盒的形状、尺寸、外表图案等．
新知二 制作立体图形
将墨水盒抽象为长方体，如图所示.
各小组按照自己的设计思路，在一张软纸上设计包装盒的平面草图，裁纸、折叠，观察效果.可以不断调整设计，直至达到设计要求.
各小组在硬纸板上按照设计方案，画好包装盒的平面展开图，注意要预留出粘合的地方，适当剪去棱角.可以在平面图上进行美术设计，比如写上小组成员的个性签名.
裁下设计好的平面图形，折叠并粘合，各小组展示成果.
设计制作一个正五棱柱形状（底面是 5 条边都相等、5个角都相等的五边形）的包装纸盒.
设计制作一个圆柱形状的包装纸盒.
1.如图为一无盖长方体盒子的展开图(重叠部分不计)，可知该无盖长方体的容积为( )A.4 B.6 C.8 D.12
解：长方体的高是1，宽是3-1=2，长是6-2=4，长方体的容积是4×2×1=8．
2.如图是一个长方体的表面展开图,每个面上都标注了字母和数据，请根据要求回答： (1) 如果 A 面在长方体的底部,那么 面会在上面；(2) 求这个长方体的表面积和体积．
解：(2) 这个长方体的表面积是 2×(1×3+1×2+2×3)=22 (平方米)．体积是 1×2×3=6 (立方米)．
3.如图，一个长方体的表面展开图中四边形 ABCD 是正方形(正方形的四个角都是直角、四条边都相等)，则根据图中数据可得原长方体的体积是 cm3．
解：因为四边形 ABCD 是正方形，所以AB=AE= 10÷2 =5 cm，所以立方体的高为 (7-5)÷2=1 (cm)，所以EF=5-1=4(cm)，所以原长方体的体积是 5×4×1=20(cm3)．
面、棱的大小、位置关系
展开图中面的位置与立体图形中的位置的对应关系
1．若∠AOB＝40°，∠BOC＝20°，则∠AOC的度数为( )A．60° B．20°C．20°或60° D．40°或80°
3．已知平面内有A，B，C，D四个点，过其中任意两点画一条直线，最多可以画出几条直线？请你画图说明.
解：①当A，B，C，D四个点在同一条直线上时，只能画出一条直线，如图1所示；②当A，B，C，D四个点中有三个点在同一条直线上(假设B，C，D三点在同一条直线上)时，可以画出4条直线，如图2所示；③当A，B，C，D四个点中任意三个点都不在同一条直线上时，可以画出6条直线，如图3所示．综上所述，最多可以画出1或4或6条直线．
4．已知线段AB＝12 cm，直线AB上有一点C，且BC＝6 cm，M是线段AC的中点，求线段AM 的长．
5．已知：如图，OC是∠AOB的平分线．(1)当∠AOB＝60°时，求∠AOC的度数；(2)在(1)的条件下，∠EOC＝90°，请在图中补全图形，并求∠AOE的度数；(3)当∠AOB＝α，∠EOC＝90°时，直接写出∠AOE的度数．(用含α的式子表示)
7．如图，线段AB上顺次有三个点C，D，E，把线段AB分为2∶3∶4∶5四部分，且AB＝28.(1)求线段AE的长；(2)若M，N分别是DE，EB的中点，求线段MN的长度．
8．如图，∠AOC和∠BOD都是直角．(1)图中与∠BOC互余的角有_______和________；(2)∠AOD与∠BOC互补吗？为什么？(3)若∠AOB∶∠AOD＝3∶13，求∠BOC与∠AOD的度数．
解：(2)∠AOD与∠BOC互补，理由：因为∠AOC和∠BOD都是直角，所以∠AOB＋∠BOC＝∠COD＋∠BOC＝90°，又因为∠AOD＝∠AOB＋∠BOC＋∠COD，所以∠AOD＋∠BOC＝∠AOB＋∠BOC＋∠COD＋∠BOC＝∠AOC＋∠BOD＝180°，所以∠AOD与∠BOC互补．(3)设∠AOB＝3x°，则∠AOD＝13x°，所以∠BOD＝∠AOD－∠AOB＝13x－3x＝10x＝90，解得x＝9，所以∠AOD＝13x°＝117°，由(2)可知∠AOD与∠BOC互补，所以∠BOC＝180°－117°＝63°.
9．如图，已知点C，D在线段AB上，M，N分别是AC，BD的中点．(1)若AB＝20，CD＝4，求MN的长；(2)若AB＝a，CD＝b，请用含有a，b的式子表示出MN的长．