广东省惠州市2022年八年级上学期期末数学试卷解析版

 八年级上学期期末数学试题

一、单选题

1．下列图形中有稳定性的是（　　）

A． B．

C． D．

2．若，则a的取值正确的是（　　）

A． B． C． D．

3．下列运算中，正确的是（　　）

A． B．

C． D．

4．如图，在中，是的平分线，，垂足为E．若，则的长为（　　）

A． B． C． D．

5．一个n边形的各内角都等于，则n等于（　　）

A．5 B．6 C．7 D．8

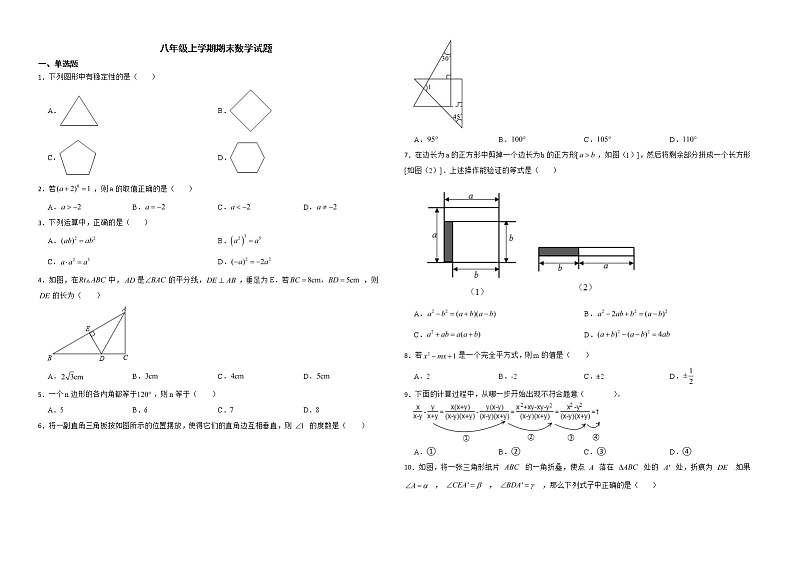
6．将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则 的度数是（　　）  

A． B． C． D．

7．在边长为a的正方形中剪掉一个边长为b的正方形[，如图（1）]，然后将剩余部分拼成一个长方形[如图（2）]．上述操作能验证的等式是（　　）

A． B．

C． D．

8．若是一个完全平方式，则m的值是（　　）

A．2 B．-2 C．±2 D．

9．下面的计算过程中，从哪一步开始出现不符合题意（        ）． 

A．① B．② C．③ D．④

10．如图，将一张三角形纸片 的一角折叠，使点 落在 处的 处，折痕为 .如果 ， ， ，那么下列式子中正确的是（　　） 

A． B．

C． D．

二、填空题

11．五边形的外角和等于　     　°．

12．若，则　     　．

13．计算：　        　．

14．化简：　     　．

15．如图，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则∠ABC+∠DFE=　     　 度．

16．在一自助夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200m到达B地，再沿北偏东30°方向走，恰能到达目的地C（如图），那么，由此可知，B、C两地相距　     　 m．

17．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则 周长的最小值为　     　. 

三、解答题

18．分解因式：．

19．如图，点B，C，E，F在同一直线上，，，，垂足分别为C，F，．求证：．

20．某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450机器所需时间相同，求该工厂原来平均每天生产多少台机器？

21．已知实数a，b满足，求的值．

22．如图，在中，，D为中点，平分交于点E，过点E作交于点F．

（1）若，求的度数；

（2）求证：．

23．如图，在平面直角坐标系中，已知，点M与关于直线l成轴对称．

（1）在题图中画出直线l及线段关于直线l对称的线段；

（2）求的面积．

24．已知：．

（1）化简A；

（2）若点与点关于y轴对称，求A的值；

（3）关于x的方程的解为正数，求k的取值范围．

25．如图， 和 中， ， 与 交于点P（不与点B，C重合），点B，E在 异侧， 、 的平分线相交于点I. 

（1）当 时，求 的长； 

（2）求证： ； 

（3）当 时， 的取值范围为 ，求m，n的值. 

答案解析部分

1．【答案】A

【知识点】三角形的稳定性

【解析】【解答】解：根据三角形具有稳定性，可得四个选项中只有三角形具有稳定性．

故答案为：A．

【分析】考查三角形具有稳定性

2．【答案】D

【知识点】0指数幂的运算性质

【解析】【解答】解：∵，

∴，

解得，，

故答案为：D．

【分析】根据a0，得出。

3．【答案】C

【知识点】同底数幂的乘法；积的乘方；幂的乘方

【解析】【解答】，故A不符合题意；

，故B不符合题意；

，故C符合题意；

，故D不符合题意；

故答案为：C．

【分析】根据积的乘方，幂的乘方运算法则得出，正确答案为C。

4．【答案】B

【知识点】角平分线的性质

【解析】【解答】解：由已知：，，是的平分线，

，

，

，

故答案为：B．

【分析】角平线的性质到两边的距离相等，得出DE=BC，再得出DE=3cm。

5．【答案】B

【知识点】多边形内角与外角

【解析】【解答】解：∵n边形的各内角都等于120°，

∴每一个外角都等于180°-120°=60°，

∴边数n=360°÷60°=6．

故答案为：B．

【分析】多边形的外角和是，一个外角是60°，得出边数是6。

6．【答案】C

【知识点】三角形内角和定理；三角形的外角性质

【解析】【解答】解：由题意得，∠2=45°，∠4=90°-30°=60°，
∴∠3=∠2=45°，
由三角形的外角性质可知，∠1=∠3+∠4=105°。
故答案为：C
【分析】三角形的外角等于不相邻的两个内角之和。
 

7．【答案】A

【知识点】平方差公式及应用；平方差公式的几何背景

【解析】【解答】由图可知，大正方形的面积=，剪掉的正方形的面积=，

∴剩余面积=，

∵拼成长方形的长=，宽=，

∴面积=，

∴．

故答案为：A

【分析】利用图形的面积切割转化相等，证得平方差公式。

8．【答案】C

【知识点】完全平方公式及运用

【解析】【解答】解：∵多项式x2-mx+1是一个完全平方式，

∴x2-mx+1＝（x+1）2或x2-mx+1＝（x﹣1）2，

即x2-mx+1＝x2+2x+1或x2-mx+1＝x2﹣2x+1，

∴m＝-2或m＝2．

故答案为：C．

【分析】考查完全平方公式，展开对应系数相等可得m＝-2或m＝2。

9．【答案】B

【知识点】分式的加减法

【解析】【解答】解：

．

故从第②步开始出现不符合题意．

故答案为：B．

【分析】直接利用分式的加减运算法则计算得出答案．

10．【答案】A

【知识点】三角形的外角性质；轴对称的性质

【解析】【解答】如图：

由折叠得：∠A=∠A'，

∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，

∵∠A=α，∠CEA′=β，∠BDA'=γ，

∴∠BDA'=γ=α+α+β=2α+β，

故答案为：A.

【分析】根据三角形的外角得：∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，代入已知可得结论.

11．【答案】360

【知识点】多边形内角与外角

【解析】【解答】五边形的外角和是360°．

故选B．

【分析】根据多边形的外角和等于360°解答．

12．【答案】2

【知识点】平方差公式及应用

【解析】【解答】解：∵，

∴，

∵，

∴，

故答案为：2．

【分析】利用平方差公式展开，把，代入解得答案为2。

13．【答案】

【知识点】分式的约分；积的乘方

【解析】【解答】解：原式=，

故答案为：．

【分析】商的乘方法则可得。

14．【答案】a

【知识点】分式的约分；分式的通分；最简分式

【解析】【解答】解：，

=，

=，

=，

=；

故答案为：a．

【分析】考查分式的通分，先找最简公分母，通分，再约分化简。

15．【答案】90

【知识点】全等三角形的应用

【解析】【解答】解：∵△ABC与△DEF均是直角三角形，BC=EF，AC=DF

∴Rt△ABC≌Rt△DEF（HL）

∴∠ABC=∠DEF

∵∠DEF+∠DFE=90°

∴∠ABC+∠DFE=90°．

故填90

【分析】由图可得，△ABC与△DEF均是直角三角形，由已知可根据HL判定两三角形全等，再根据全等三角形的对应角相等，不难求解．　

16．【答案】200

【知识点】解直角三角形的应用﹣方向角问题

【解析】【解答】解：由已知得：

∠ABC=90°+30°=120°，

∠BAC=90°﹣60°=30°，

∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣120°﹣30°=30°，

∴∠ACB=∠BAC，

∴BC=AB=200．

故答案为：200．

【分析】首先把实际问题转化为直角三角形问题来解决，由已知可推出∠ABC=90°+30°=120°，∠BAC=90°﹣60°=30°，再由三角形内角和定理得∠ACB=30°，从而求出B、C两地的距离．

17．【答案】10

【知识点】三角形的面积；等腰三角形的性质；轴对称的应用-最短距离问题

【解析】【解答】解：连接AD，

∵△ABC是等腰三角形，点D是BC边的中点，

∴AD⊥BC，

∴S△ABC= BC•AD= ×4×AD=16，解得AD=8，

∵EF是线段AB的垂直平分线，

∴点B关于直线EF的对称点为点A，

∴AD的长为CM+MD的最小值，

∴△CDM的周长最短=（CM+MD）+CD=AD+ BC=8+ ×4=8+2=10.

故答案为：10.

【分析】连接AD，根据等腰三角形的三线合一得出AD⊥BC，根据△ABC的面积=16，由面积计算公式列出方程，求解得出AD的长，根据轴对称的性质得出点B关于直线EF的对称点为点A，根据垂线段最短得出AD的长为CM+MD的最小值，进而即可根据三角形的周长计算方法即可算出答案。

18．【答案】解：（x-4）（x+1）+3x

=x2-3x-4+3x

=x2-4

=（x+2）（x-2）．

【知识点】多项式乘多项式；因式分解﹣运用公式法

【解析】【分析】根据多项式乘多项式展开，合并同类型，再根据平方差公式因式分解得出 （x+2）（x-2） 。

19．【答案】证明：∵，

∴即，

在Rt△ABC和Rt△DEF中

∴Rt△ABC≌Rt△DEF（HL），

∴AC=DF．

【知识点】直角三角形全等的判定（HL）

【解析】【分析】证明 Rt△ABC≌Rt△DEF（HL） ，得出 AC=DF 。

20．【答案】解：设该工厂原来平均每天生产x台机器，则现在平均每天生产(x+50)台机器．

根据题意得，解得x=150．

经检验知x=150是原方程的根．

答：该工厂原来平均每天生产150台机器．

【知识点】分式方程的实际应用

【解析】【分析】找出等量关系式， 现在生产600台机器所需时间与原计划生产450机器所需时间相同 ，列方程 解得x=150 。

21．【答案】解：∵a+b=2，ab=，

∴

=

=

=

=

=4--1

=．

【知识点】多项式乘多项式；整式的混合运算

【解析】【分析】分式约分化简，平方差公式，完全平方公式的变形得出 ，代数得出 。

22．【答案】（1）解：，

，

，

又D为中点，根据等腰三角形三线合一的性质有：

；

（2）证明：已知平分，

，

又，

，

，

是等腰三角形，

．

【知识点】三角形的角平分线、中线和高；等腰三角形的性质

【解析】【分析】 (1)根据等腰三角形三线合一的性质得出 ；
(2)已知平分  得出 ，根据 ，得出 ，最后证得 。

23．【答案】（1）解：直线l如图所示；线段关于直线l对称的线段如图所示；

（2）解：的面积为：．

【知识点】轴对称图形；作图﹣轴对称

【解析】【分析】 (1)、 根据轴对称的性质画出直线  ；
(2)、三角形面积等于底乘高得出 。

24．【答案】（1）解：原式=

=

=；

（2）解：点关于y轴对称，纵坐标不变，横坐标变为相反数，

，

将代入原式：；

（3）解：由题：（），

，

（），

解得且．

【知识点】分式的约分；分式的混合运算

【解析】【分析】 (1)分式通分，因式分解，约分化简得 ；
(2)点关于y轴对称，纵坐标不变，横坐标变为相反数 ，得出x=4，将代入原式： ；
(3)由（）解得且 。

25．【答案】（1）解：∵ ， 

∴△ABP为直角三角形，

∵∠B=30°，AB=6，

∴AP=3，

∴PD=AD-AP=3；

（2）证明：在△ABC和△ADE中，

，

∴△ABC≌△ADE（SAS），

∴∠BAC=∠DAE，

∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE；

（3）解：设∠BAP=α，则∠PAC=90°-α，

∵∠B=30°，∠BAC=90°，

∴∠BCA=180°-30°-90°=60°，

∵AI、CI分别平分∠PAC，∠PCA，

∴∠IAC= ∠PAC= （90°-α）=45°- α，∠ICA= ∠PCA=30°，

∴∠AIC=180°-（∠IAC+∠ICA）

=180°-（45°- α+30°）

=105°+ α，

∵0°＜α＜90°，

∴105°＜ α+105°＜150°，即105°＜∠AIC＜150°，

∴m=105，n=150.

【知识点】三角形内角和定理；含30°角的直角三角形；三角形全等的判定（SAS）；角平分线的定义

【解析】【分析】（1）利用垂直的定义可推出△ABP是直角三角形，利用30°角所对的直角边等于斜边的一半，可求出AP的长；然后根据PD=AD-AP，可求出PD的长；
（2）利用SAS证明△ABC≌△ADE，利用全等三角形的对应角相等，可证得∠BAC=∠DAE，由此可推出结论；
（3）设∠BAP=α，则∠PAC=90°-α， 利用三角形的内角和定理求出∠BCA=60°，再利用角平分线的定义可得到∠IAC和∠ICA的度数；再根据∠AIC=180°-（∠IAC+∠ICA），可表示出∠AIC的度数，然后根据0°＜α＜90°，可得到m，n的值.