
《高考数学二轮复习培优》第09讲空间几何体的三视图
展开
这是一份《高考数学二轮复习培优》第09讲空间几何体的三视图,共22页。教案主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题
1.(2017年高考北京卷理)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A. 3 B. 2 C. 2 D. 2
【答案】B
【解析】几何体是四棱锥,如图.
最长的棱长为补成的正方体的体对角线,即该四棱锥的最长棱的长度,故选B.
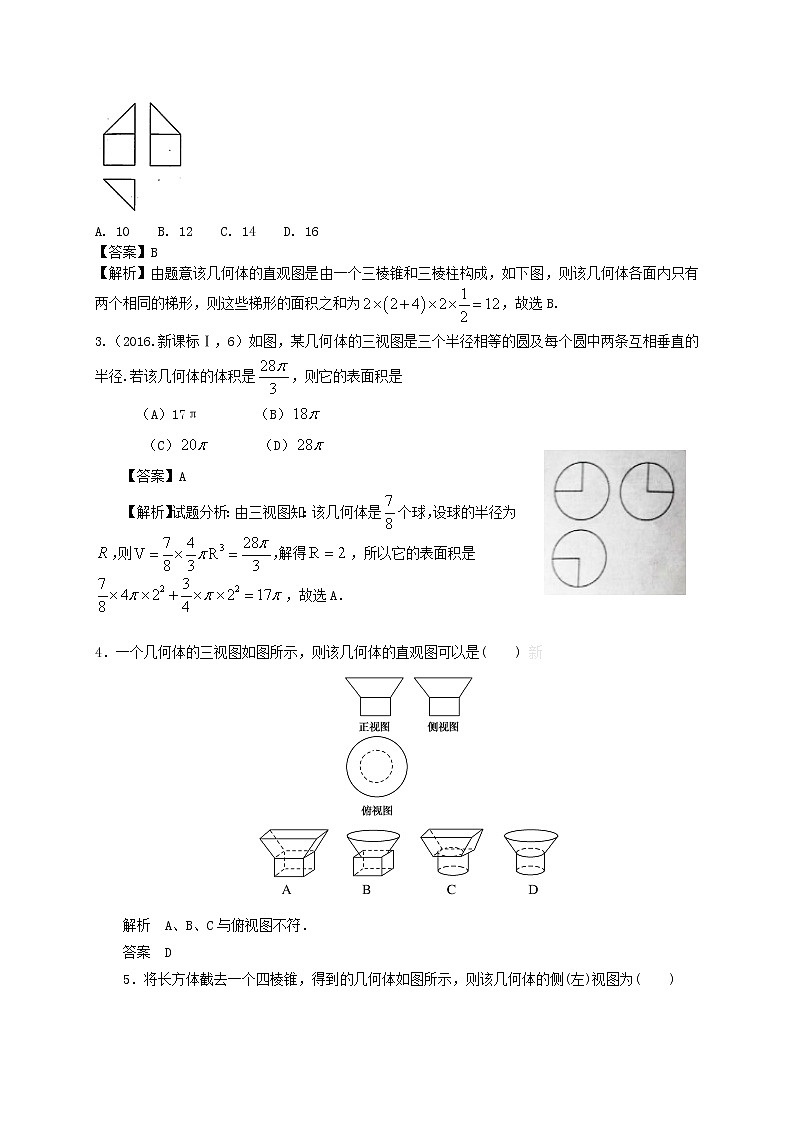
2. (2017年高考全国1卷理)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为
A. 10 B. 12 C. 14 D. 16
【答案】B
【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为,故选B.
3.(2016.新课标Ⅰ,6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是
(A)17π (B)
(C) (D)
【答案】A
【解析】试题分析:由三视图知:该几何体是个球,设球的半径为,则,解得,所以它的表面积是,故选A.
4.一个几何体的三视图如图所示,则该几何体的直观图可以是( ) 新
解析 A、B、C与俯视图不符.
答案 D
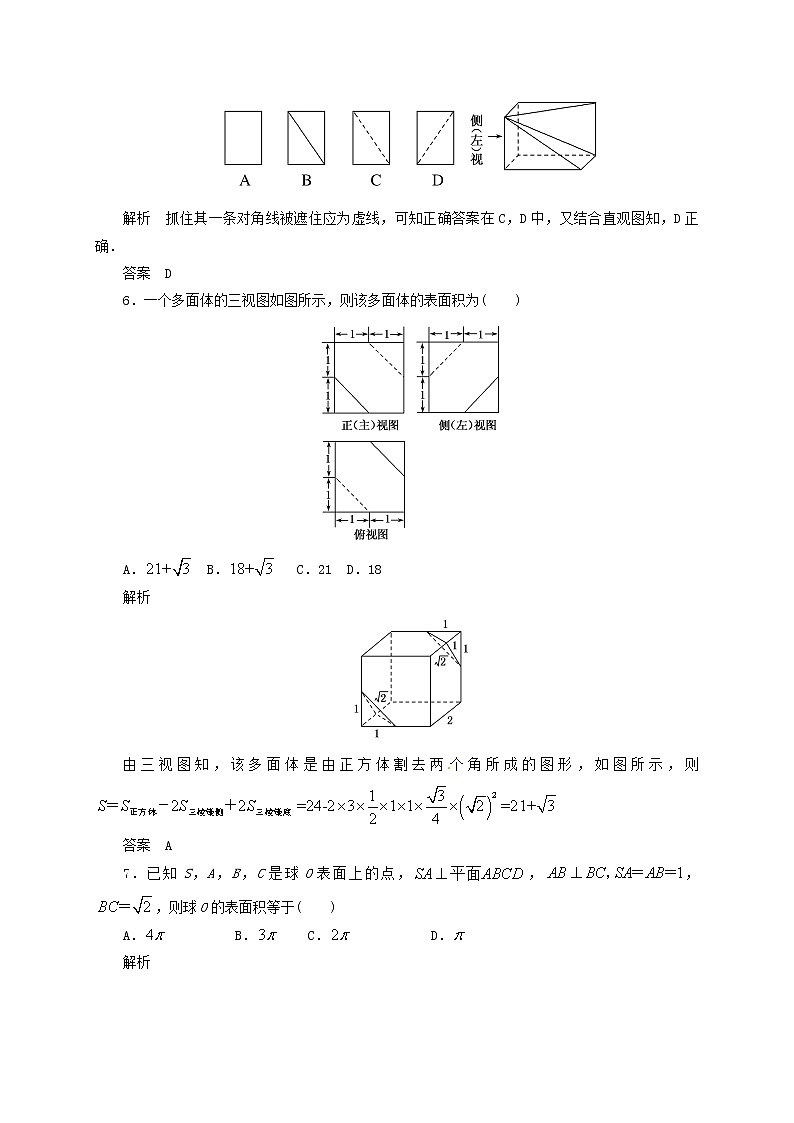
5.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧(左)视图为( )
解析 抓住其一条对角线被遮住应为虚线,可知正确答案在C,D中,又结合直观图知,D正确.
答案 D
6.一个多面体的三视图如图所示,则该多面体的表面积为( )
A. B. C.21 D.18
解析
由三视图知,该多面体是由正方体割去两个角所成的图形,如图所示,则
答案 A
7.已知S,A,B,C是球O表面上的点,,,,则球O的表面积等于( )
A. B. C. D.
解析
如图所示,由知,AC为过A,B,C,D四点小圆直径,
所以.
又
设为SA,AB,BC为棱长构造的长方体,
得体对角线长为
所以R=1,球O的表面积.故选A.
答案 A
8.一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )
A.1 B.2 C.3 D.4
解析
由三视图可得原石材为如图所示的直三棱柱且,,.若要得到半径最大的球,则此球与平面,,相切,故此时球的半径与△ABC内切圆的半径相等,故半径故选B.
答案 B
9.点A,B,C,D均在同一球面上,其中△ABC是正三角形,,,则该球的体积为( )
A. B. C.D.
解析
新$课$标$第$一$网
如图所示,O1为三角形ABC的外心,过O做
∴,
∴
∴E为DA的中点.∵,
∴,∴.
∴∴∴
答案 A
二、填空题
10.某四棱锥的三视图如图所示,该四棱锥的体积是________.
w w w .x k b 1.c m
解析
由三视图可知,四棱锥的高为2,底面为直角梯形.其中,,,所以四棱锥的体积为
答案
11.如图,在三棱柱中,D,E,F分别是AB,AC,AA1的中点,设三棱锥的体积为V1,三棱柱的体积为V2,则________.
解析 设三棱柱的高为h,底面三角形ABC的面积为S,则,即
答案
12.在四面体中,,A,,则四面体的外接球的表面积为________.
解析 构造一个长方体,使得它的三条面对角线分别为4、5、6,设长方体的三条边分别为x,y,z,则,而长方体的外接球就是四面体的外接球,所以
答案
三、解答题
13.下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图.右边两个是其正(主)视图和侧(左)视图.
(1)请在正(主)视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程).
(2)求该多面体的体积(尺寸如图).
解 (1)作出俯视图如图所示.
(2)依题意,该多面体是由一个正方体()截去一个三棱锥()得到的,所以截去的三棱锥体积
==,
正方体体积V正方体xkb1.cm
所以所求多面体的体积
14.
如图,四棱柱中,四边形ABCD为梯形,,且.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比.
解 (1)证明:因为,,,
所以从而平面A1CD与这两个平面的交线相互平行,即.
故△QBC与△A1AD的对应边相互平行,于是.
所以即Q为BB1的中点.新-课-标-第-一-网
(2)如图,连接QA,QD.
设,梯形的高为d,四棱柱被平面α所分成上下两部分的体积分别为V上和V下,,则
所以,
又,
所以.故.
B组
1.(2017年高考全国2卷)如图,网格纸上小正方形的边长为1,学 科&网粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A. B. C. D.
【答案】B
【解析】由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积,上半部分是一个底面半径为3,高为6的圆柱的一半,其体积,故该组合体的体积.故选B.
2.一个几何体的三视图如图所示,则该几何体的直观图可以是( )
答案 D
解析 由三视图可知上部是一个圆台,下部是一个圆柱,选D.
3.如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
A. B. C. D.答案 C
解析 由三视图可知几何体是如图所示的两个圆柱的组合体.其中左面圆柱的高为4 cm,底面半径为2 cm,右面圆柱的高为2 cm,底面半径为3 cm,则组合体的体积(cm3),原毛坯体积(cm3),则所求比值为
4.某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90 cm2 B.129 cm2 C.132 cm2 D.138 cm2
答案 D
解析 该几何体如图所示,长方体的长、宽、高分别为6 cm,4 cm,3 cm,直三棱柱的底面是直角三角形,边长分别为3 cm,4 cm,5 cm,所以表面积(cm2).
5.三棱锥中,D,E分别为PB,PC的中点,记三棱锥的体积为V1,的体积为V2,则_______.
解析 由于,所以,又因所以∴.
答案
6.某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为________.
答案
解析
根据三视图还原几何体,得如图所示的三棱锥
由三视图的形状特征及数据,可推知,且底面为等腰三角形,设D为AC的中点,,则,且
易得,所以最长的棱为PC,
7.已知正三棱锥P-ABC,点P,A,B,C都在半径为的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
答案
解析 如图,
作设PA=a,则,
设球的半径为R,
所以,
将代入上式,
解得,所以
8.已知一个圆锥的底面半径为R,高为H,在其内部有一个高为x的内接圆柱.
(1)求圆柱的侧面积;
(2)x为何值时,圆柱的侧面积最大?
解 (1)
作圆锥的轴截面,如图所示.
因为,所以所以
(2)因为,
所以当时,S圆柱侧最大.
故当即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.
9.如图,在三棱柱中,侧棱垂直于底面,,E,F分别是A1C1,BC的中点.
(1)求证:
(2)求证:
(3)求三棱锥的体积.
(1)证明
在三棱柱中,
,
所以.
又因为,
所以又因为,
所以.
(2)证明 取AB的中点G,连接EG,FG.
因为E,F分别是A1C1,BC的中点,所以因为,且所以,
所以四边形为平行四边形.
所以
又因为
所以.
(3)解 因为所以所以三棱锥E-ABC的体积
10.如图,四棱锥中,底面为矩形,,E为PD的中点.
(1)证明:
(2)设二面角为60°,,求三棱锥的体积.
解 (1)连接BD交AC于点O,连接EO.
因为为矩形,所以O为BD的中点.
又E为PD的中点,所以
所以(2)因为,为矩形,所以AB,AD,AP两两垂直.
如图,以A为坐标原点,eq \(AB,\s\up6(→))的方向为x轴的正方向,|eq \(PA,\s\up6(→))|为单位长,建立空间直角坐标系.
则,, 设,则,|b|1
设为平面ACE的法向量,
则即
可取
又为平面DAE的法向量,
由题设即 解得.因为E为PD的中点,所以三棱锥的高为eq \f(1,2).三棱锥的体积
11.如图,在Rt△ABC中,,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=30°.xkb1
(1)求证:;
(2)试问:当点E在何处时,四棱锥的侧面的面积最大?并求此时四棱锥的体积.
解 (1)证明:
又,
即
又
∴
∴.
(2)设∴
当且仅当时,S△PEB的面积最大.
此时,
由(1)知∴
在平面中,作于O,
则.
即PO为四棱锥的高.
又 w W w .X k b 1.c O m
∴
C组
1.(2017年高考全国3卷文)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为
A. B. C. D.
【答案】B
【解析】绘制圆柱的轴截面如图所示,由题意可得: ,
结合勾股定理,底面半径,
由圆柱的体积公式,可得圆柱的体积是,故选B.
2.某几何体的三视图如图所示,则该几何体的表面积为( )
A.54 B.60 C.66 D.72
答案 B
解析 由俯视图可以判断该几何体的底面为直角三角形,由正视图和侧视图可以判断该几何体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的.在长方体中分析还原,如图(1)所示,故该几何体的直观图如图(2)所示.在图(1)中,直角梯形ABPA1的面积为计算可得A1P=5.直角梯形BCC1P的面积为.因为,所以故Rt△A1PC1的面积为
又Rt△ABC的面积为,矩形ACC1A1的面积为,故几何体的表面积为.
3.两球O1和O2在棱长为1的正方体的内部,且互相外切,若球O1与过点A的正方体的三个面相切,球O2与过点C1的正方体的三个面相切,则球O1和球O2的表面积之和的最小值为( )
A. B. C. D.
答案 A
解析 设球O1,O2的半径分别为r1,r2,
由题意知,
而,,
∵∴,
从而
4.已知球的直径,A,B是该球球面上的两点,,则棱锥的体积为( )
A.B. C. D.1
答案 C
解析
如图,过A作AD垂直SC于D,连接BD.
由于SC是球的直径,所以,又,又SC为公共边,所以.由于所以.
由此得SC⊥平面ABD.所以由于在中,所以由于同理在中也有.又,所以△ABD为正三角形,
所以所以选C.
5.某几何体三视图如图所示,则该几何体的体积为( )
B. C. D.
答案 B
解析
这是一个正方体切掉两个eq \f(1,4)圆柱后得到的几何体,
如图,几何体的高为2,
6.已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得几何体的体积为( )
A. B. C. D.
答案 C
解析
由三视图确定该几何体是一个半球体与三棱锥构成的组合体,如图,其中AP,AB,AC两两垂直,且,故AS所以三棱锥的体积,又Rt△ABC是半球底面的内接三角形,所以球的直径,解得,所以半球的体积,故所求几何体的体积
7.有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a的取值范围是
(A) (B)(C) (D)
【答案】A
【命题立意】本题考查了学生的空间想象能力以及灵活运用知识解决数学问题的能力。
【解析】根据条件,四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架,有以下两种情况:(1)地面是边长为2的正三角形,三条侧棱长为2,a,a,如图,此时a可以取最大值,可知,,则有,即,即有a0;
综上分析可知
8.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于 .
【答案】
【解析】由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为
,侧面积为,所以其表面积为。
【命题意图】本题考查立体几何中的三视图,考查同学们识图的能力、空间想象能力等基本能力。
9.如图,在三棱锥中,三条棱,,两两垂直,且>>,分别经过三条棱,,作一个截面平分三棱锥的体积,截面面积依次为,,,则,,的大小关系为 。
【答案】
【解析】考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得。
10.在直三棱柱中,.
(1)求异面直线B1C1与AC所成角的大小;
(2)若直线A1C与平面ABC所成角为45°, 求三棱锥的体积.
解(1)因为,所以∠BCA(或其补角)即为异面直线与所成角
, ,所以,
即异面直线与所成角大小为。
(2)直三棱柱中,,所以即为直线A1C与平面ABC所成角,所以。
中,得到,中,得到,
所以
11.某高速公路收费站入口处的安全标识墩如图4所示。墩的上半部分是正四棱锥
,下半部分是长方体。图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线平面.
【解析】(1)侧视图同正视图,如下图所示.
(2)该安全标识墩的体积为:
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知, ,
又
又 ;
相关教案
这是一份《高考数学二轮复习培优》第17讲 离散型随机变量及分布列,共19页。教案主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份《高考数学二轮复习培优》第10讲 直线与平面平行,共18页。
这是一份《高考数学二轮复习培优》第08讲 导数及其应用,共24页。教案主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









