初中数学华师大版九年级上册4. 相似三角形的应用课后练习题

这是一份初中数学华师大版九年级上册4. 相似三角形的应用课后练习题，文件包含相似三角形的应用-九年级数学上册尖子生同步培优题典解析版华师大版docx、相似三角形的应用-九年级数学上册尖子生同步培优题典原卷版华师大版docx等2份试卷配套教学资源，其中试卷共95页， 欢迎下载使用。
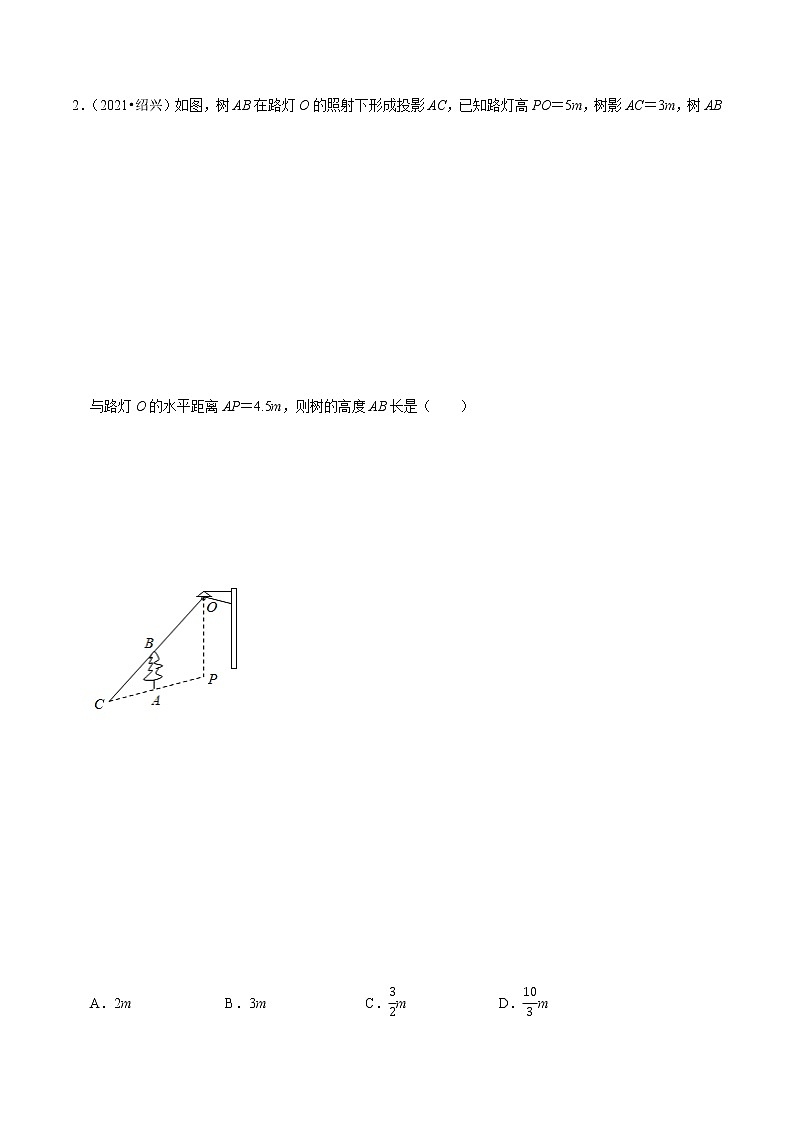
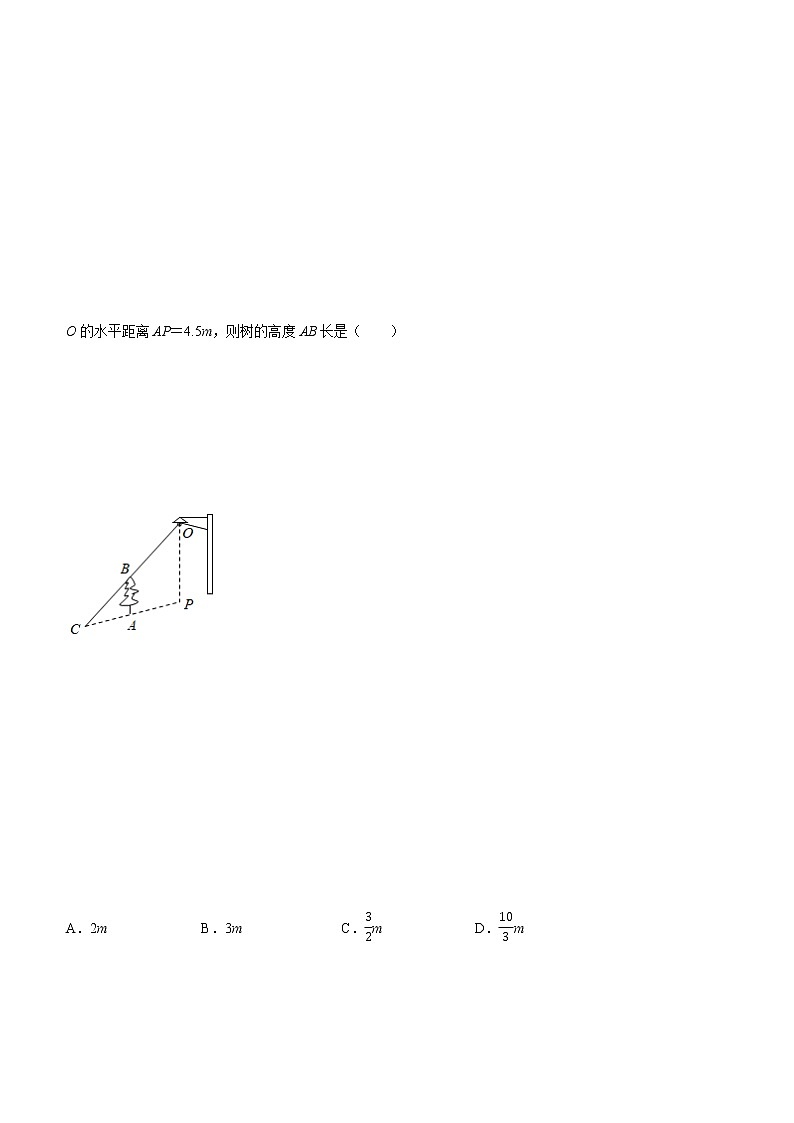
相似三角形的应用注意事项：本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置． 一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的． 1．（2020秋•海曙区期末）在同一时刻，身高1.8米的小强在阳光下的影长为0.9米，一棵大树的影长为4.6米，则树的高度为（　　）A．9.8米 B．9.2米 C．8.2米 D．2.3米选：B．2．（2021•绍兴）如图，树AB在路灯O的照射下形成投影AC，已知路灯高PO＝5m，树影AC＝3m，树AB与路灯O的水平距离AP＝4.5m，则树的高度AB长是（　　）A．2m B．3m C．m D．m【解】∵AB∥OP，∴△CAB∽△CPO，∴，∴，∴AB＝2（m），故选：A．3．（2020•新都区模拟）如图，路灯OP距地面8米，身高1.6米的小明从距离灯的底部（点O）20米的点A处，沿OA所在的直线行走14米到点B处时，人影的长度（　　）A．变长了1.5米 B．变短了2.5米 C．变长了3.5米 D．变短了3.5米【解】设小明在A处时影长为x，B处时影长为y．∵AD∥OP，BC∥OP，∴△ADM∽△OPM，△BCN∽△OPN，∴，，则，∴x＝5；，∴y＝1.5，∴x﹣y＝3.5，故变短了3.5米．故选：D．4．（2020秋•合肥期末）如图，有一块直角三角形余料ABC，∠BAC＝90°，G，D分别是AB，AC边上的一点，现从中切出一条矩形纸条DEFG，其中E，F在BC上，若BF＝4.5cm，CE＝2cm，则GF的长为（　　）A．3cm B．2cm C．2.5cm D．3.5cm选：A．5．（2021•河北）图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB＝（　　）A．1cm B．2cm C．3cm D．4cm【解】如图：过O作OM⊥CD，垂足为M，过O作ON⊥AB，垂足为N，∵CD∥AB，∴△CDO∽ABO，即相似比为，∴，∵OM＝15﹣7＝8，ON＝11﹣7＝4，∴，，∴AB＝3，故选：C．6．（2021•深圳模拟）龙翔大道旁有一根电线杆AB和一块长方形广告牌，有一天质彬突然发现在太阳光照射下，电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处，而长方形广告牌的影子刚好落在地面上E点（如图），已知BC＝5米，长方形广告牌的长HF＝4米，高HC＝3米，DE＝4米，则电线杆AB的高度是（　　）A．6.75米 B．7.75米 C．8.25米 D．10.75米选：C．7．（2021•雁塔区校级模拟）《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产．书中的第一问：今有望海岛，立两表，齐高三丈，前后相去千步，令后表与前表参相直，从前表却行一百二十三步，人目着地取望岛峰，与表末参合．从后表却行一二十七步，人目着地取望岛峰，亦与表未参合．问岛高及去表各几何？大致意思是：假设测量海岛，立两根表，高均为3丈，前后相距1000步，令后表与前表在同一直线上，从前表退行123步，人的眼睛贴着地面观察海岛，从后表退行127步，人的眼睛贴着地面观察海岛，问海岛高度及两表相距多远？想要解决这一问题，需要利用（　　）A．全等三角形 B．相似三角形 C．勾股定理 D．垂径定理选：B．8．（2021•薛城区一模）大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是（　　）A．3cm B．4cm C．6cm D．9cm【解】设蜡烛火焰的高度是xcm，由相似三角形的性质得到：．解得x＝4．即蜡烛火焰的高度是4cm．故选：B．9．（2020秋•温州期末）如图，是一块矩形场地ABCD，宽AB＝8米，长BC＝12米．若在其对角线AC，BD的延长线上取点E，F，G，H，扩建为新的矩形场地，左、右各增加了0.6米，上、下各增加了x米，则x的值为（　　）A．0.2 B．0.3 C．0.4 D．0.5【解】由题意得，AD∥EH，AB∥EF，∴△AOD∽△EOH，△AOB∽△EOF，∴，，∴，∵左、右各增加了0.6米，上、下各增加了x米，AB＝8米，BC＝12米．∴EH＝12+2×0.6＝13.2，EF＝8+2x，∴，解得：x＝0.4，故选：C．10．（2021•大渡口区模拟）如图，已知，M，N分别为锐角∠AOB的边OA，OB上的点，ON＝6，把△OMN沿MN折叠，点O落在点C处，MC与OB交于点P，若MN＝MP＝5，则PN＝（　　）A．2 B．3 C． D．选：D．二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2020秋•朝阳区校级期末）如图是用卡钳测量容器内径的示意图，现量得卡钳上A，D两个端点之间的距离为10cm，，则容器的内径是 　15cm　．答案为：15cm．12．（2020秋•北仑区期末）在“测量学校教学楼的高度”的数学活动中，小刚同学使用镜面反射法进行测量，如图所示．若a1＝1米，a2＝10米，h＝1.8米，则这个学校教学楼的高度为　18　米．答案为：18．13．（2020秋•江都区期末）如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体在暗盒中所成的像CD的高度为4cm，那么物体AB的高度应为　3　m．答案为：3．14．（2020秋•盐城期末）小明想测量出电线杆AB的高度，于是在阳光明媚的星期天，他在电线杆旁的点D处立一标杆CD，使标杆的影子DE与电线杆的影子BE部分重叠（即点E、C、A在一直线上），量得ED＝3米，DB＝6米，CD＝1.8米，则电线杆AB长＝　5.4　米．【解】∵CD∥AB，∴△ECD∽△EAB，∴ED：EB＝CD：AB，∴3：9＝1.8：AB，∴AB＝5.4米．故答案是：5.4．15．（2021•宝应县一模）《孙子算经》是中国古代经典的数学著作，其中有首歌谣，今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？其大意是，有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆，它的影长五寸（提示：1丈＝10尺，1尺＝10寸），则竹竿的长为　四丈五尺　．答案为：四丈五尺．16．（2021•闵行区二模）《九章算术》中记载了一种测距的方法．如图，有座塔在河流北岸的点E处，一棵树位于河流南岸的点A处，从点A处开始，在河流南岸立4根标杆，以这4根标杆为顶点，组成边长为10米的正方形ABCD，且A，D，E三点在一条直线上，在标杆B处观察塔E，视线BE与边DC相交于点F，如果测得FC＝4米，那么塔与树的距离AE为　25　米．答案为：25．17．（2020•文成县二模）文成县珊溪水库素有“温州大水缸”之称，现计划在水库堤坝内侧坡面上建一个水质监测站，监测站平面结构呈等腰三角形（如图△ABC，AB＝AC，底边BC所在直线平行于水平线），且一腰（AC）垂直于坡面直线GC（如图所示），中柱AE过底边BC中点D立于坡面直线GC上点E处，AB及其延长线交坡面直线GC于F，AF为一根支撑柱，另外过AE的中点M和点B做一条自动取样传送带，直达坡面直线上点G处（方便取到不同深度的水样，点M、B、G在一条直线上），测得DE＝1米，DC＝2米，则GF＝　　米（结果保留根号）．【解】∵AB＝AC，D为BC中点，∴AE⊥BC，又∵AC⊥EC，∴，即，∴AD＝4，AE＝AD+DE＝4+1＝5，∵M为AE中点，∴MEAE＝2.5，MD＝ME﹣DE＝1.5．如图，延长CB，过点G作GH⊥CB的延长线于H，则△GHB∽△MDB，∴，设GH＝3a，则BH＝4a．∵GH∥DE，∴△CHG∽△CDE，∴，即，解得a＝2，∴GH＝6，BH＝8，HC＝12，在Rt△GHC中，由勾股定理得GC6．连接BE．∵点M为Rt△ABE斜边的中点，∴∠BMD＝2∠BAM＝∠BAC，∴tan∠BAC＝tan∠BMD，在Rt△ACF中，AC＝2，∴CF＝AC•tan∠BAC＝2，∴GF＝GC﹣CF＝6．故答案为：．18．（2020•泰顺县二模）图1是一种手机托架，使用该手机托架示意图如图3所示，底部放置手机处宽AB＝1.2厘米，托架斜面长BD＝6厘米，它有C到F共4个档位调节角度，相邻两个档位间的距离为0.8厘米，档位C到B的距离为2.4厘米．将某型号手机置于托架上（图2），手机屏幕长AG是15厘米，O是支点且OB＝OE＝2.5厘米（支架的厚度忽略不计）．当支架调到E档时，点G离水平面的距离GH为　　厘米；当支架从E档调到F档时，点D离水平面的距离下降了　　厘米．答案为，．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2020秋•涟水县期末）新建马路需要在道路两旁安装路灯、种植树苗．如图，某道路一侧路灯AB在两棵同样高度的树苗CE和DF之间，树苗高2m，两棵树苗之间的距离CD为18m，在路灯的照射下，树苗CE的影长CG为1m，树苗DF的影长DH为3m，点G、C、B、D、H在一条直线上．求路灯AB的高度．【解】设BC的长度为xm，由题意可知CE∥AB∥DF，如图，∵CE∥AB，DF∥AB，∴△GCE∽△GBA，△HDF∽△HBA∴，即；，即，∴，解得x＝4.5，∴，解得AB＝11．答：路灯AB的高度为11m．20．（2021春•工业园区期末）如图，安装路灯AB的路面CD比种植树木的地面PQ高1.2m（CP＝1.2m）身高1.8m的小明MN站在距离C点15m远的路面上．在路灯的照射下，路基CP留在地面上的影长EP为0.4m，小明留在路面上的影长NF为3m，求路灯AB的高度．【解】如图，设AB＝xm，CB＝ym．∵，，∴，解得，经检验是分式方程的解，∴AB＝9（m），答：灯AB的高度为9m．21．（2020秋•盐城期末）如图，小明想测量河对岸建筑物AB的高度，在地面上C处放置了一块平面镜，然后从C点向后退了2.4米至D处，小明的眼睛E恰好看到了镜中建筑物A的像，在D处做好标记，将平面镜移至D处，小明再次从D点后退2.52米至F处，眼睛G恰好又看到了建筑物顶端A的像，已知小明眼睛距地面的高度ED，GF均为1.6米，求建筑物AB的高度．（注：图中的左侧α，β为入射角，右侧的α，β为反射角）【解】设AB为xm，BC为ym，根据题意知，△ABC∽△DEC，有①．△ABD∽△GFD，有②．联立①②，得x＝32．答：建筑物AB的高度为32m．22．（2021•海曙区模拟）如图是某公园的一台滑梯，滑梯着地点B与梯架之间的距离BC＝4m．（1）现在某一时刻测得身高1.8m的小明爸爸在阳光下的影长为0.9m，滑梯最高处A在阳光下的影长为1m，求滑梯的高AC；（2）若规定滑梯的倾斜角（∠ABC）不超过30°属于安全范围，请通过计算说明这架滑梯的倾斜角是否符合安全要求？【解】（1）由题意可得：，解得：AC＝2（m），答：滑梯的高AC为2m； （2）∵tan∠ABCtan30°，∴∠ABC＜30°，∴这架滑梯的倾斜角符合安全要求．23．（2021•渭滨区一模）九年级活动小组计划利用所学的知识测量操场旗杆高度．测量方案如下：如图，小卓在小越和旗杆之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小卓看着镜面上的标记，他来回走动，走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合，这时测得小卓眼睛与地面的高度ED＝1.5米，CD＝1米，然后在阳光下，小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合，测得FG＝1.6米，FH＝3.2米，已知AB⊥BM，ED⊥BM，GF⊥BM若测量时所使用的平面镜的厚度忽略不计，请你根据图中提供的相关信息求出旗杆的高AB．【解】由题意可得：∠BCA＝∠ECD，∠ABC＝∠EDC，故△ABC∽△EDC，则，即1.5，∴AB＝1.5BC，∵GF∥AB，∴△GFH∽△ABH，∴，∴，解得：BC＝10，故AB＝1.5BC＝15米．答：旗杆的高AB为15米．24．（2021•韩城市一模）青龙寺是西安最著名的樱花观赏地，品种达到了13种之多，每年3、4月陆续开放的樱花让这里成为了花的海洋．一天，小明和小刚去青龙寺游玩，想利用所学知识测量一棵樱花树的高度（樱花树四周被围起来了，底部不易到达）．小明在F处竖立了一根标杆EF，小刚走到C处时，站立在C处看到标杆顶端E和树的顶端B在一条直线上．此时测得小刚的眼睛到地面的距离DC＝1.6米；然后，小刚在C处蹲下，小明平移标杆到H处时，小刚恰好看到标杆顶端G和树的顶端B在一条直线上，此时测得小刚的眼睛到地面的距离MC＝0.8米．已知EF＝GH＝2.4米，CF＝2米，FH＝1.6米，点C、F、H、A在一条直线上，点M在CD上，CD⊥AC，EF⊥AC，GH⊥AC，AB⊥AC．根据以上测量过程及测量数据，请你求出这棵樱花树AB的高度．【解】过点D作DP⊥AB于点P，交EF于点N，过点M作MQ⊥AB于点Q，交GH于点K，由题意可得：DP＝MQ＝AC，DN＝CF＝2米，MK＝CH，AP＝DC＝1.6米，AQ＝HK＝MC＝0.8米．∵∠EDN＝∠BDP，∠END＝∠BPD＝90°，∠GMK＝∠BMQ，∠GKM＝BQM＝90°，∴△DEN∽△DBP，△GMK∽△BMQ，∴，．∴，．∴AB＝8.8（米）．答：这棵樱花树AB的高度是8.8米．