期中考试押题卷（测试范围：第一～三章）-高一数学新教材同步配套教学讲义（人教A版2019必修第一册）

这是一份期中考试押题卷（测试范围：第一～三章）-高一数学新教材同步配套教学讲义（人教A版2019必修第一册），文件包含期中考试押题卷测试范围第一～三章解析版docx、期中考试押题卷测试范围第一～三章原卷版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
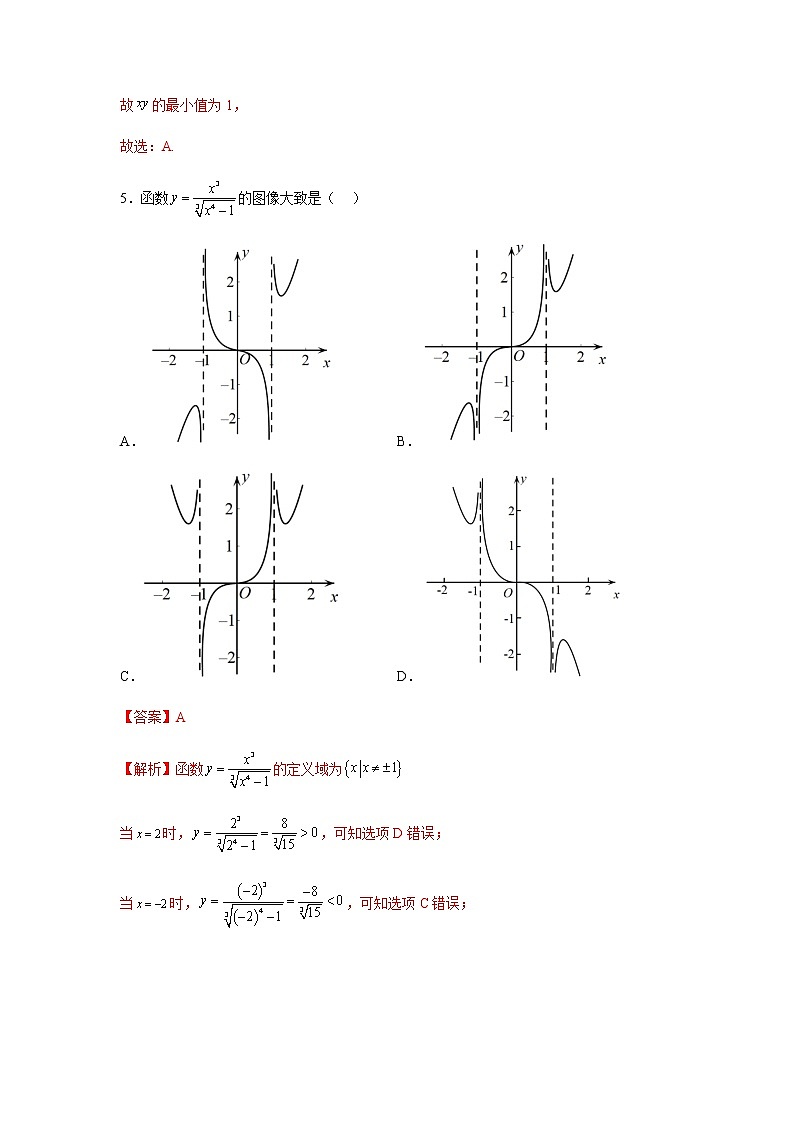
期中考试押题卷（考试时间：120分钟  试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效．3．回答第Ⅱ卷时，将答案写在答题卡上．写在本试卷上无效．4．测试范围：人教A版2019必修第一册第一章、第二章、第三章5．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。1．下列四个写法：①；②；③；④.错误写法的个数为（    ）A．1 B．2 C．3 D．4【答案】B【解析】①是集合，是集合，不能用，故错误；②规定空集是任何集合的子集，所以，故正确；③，同时也满足子集的定义，故正确；④空集中无元素，故，故错误，故选：B2．已知，下列四个条件中，使“”成立的必要而不充分的条件是（    ）A． B． C． D．【答案】A【解析】使成立的必要不充分条件，即能得到哪个条件，而由该条件得不到，故对于A选项，可以得到，反之不成立，故是必要而不充分的条件；对于B选项，可以得到，反之不成立，故是的充分不必要条件；对于C选项，是的既不充分也不必要条件；对于D选项，是的充分不必要条件.故选：A．3．已知，则的解析式为（    ）A． B．C． D．【答案】C【解析】因为令，所以 所以故选：C.4．若实数满足：，则的最小值为（    ）A．1 B．2 C．3 D．4【答案】A【解析】因为，所以，由基本不等式可得，故，解得或（舍），即当且仅当时等号成立，故的最小值为1，故选：A.5．函数的图像大致是（    ）A． B．C． D．【答案】A【解析】函数的定义域为当时，，可知选项D错误；当时，，可知选项C错误；当时，，可知选项B错误，选项A正确.故选：A6．若不等式对一切恒成立，则的取值范围是（  ）A． B． C． D．【答案】C【解析】当时，原式化为，显然恒成立；当时，不等式对一切恒成立，则有且，解得.综上可得，.故选：C7．已知函数是定义在R上的偶函数，若，，且，都有成立，则不等式的解集为（    ）A． B． C． D．【答案】C【解析】令，因为函数是定义在R上的偶函数，所以，即是定义在R上奇函数．又，，且，都有成立，所以在上单调递减，又是定义在R上奇函数，所以在R上单调递减，所以，即，所以，解得．故A，B，D错误.故选：C．8．设是实数集的一个非空子集，如果对于任意的与可以相等，也可以不相等），且，则称是“和谐集”.则下列命题中为假命题的是（    ）.A．存在一个集合，它既是“和谐集”，又是有限集B．集合是“和谐集”C．若都是“和谐集”，则D．对任意两个不同的“和谐集”，总有【答案】D【解析】A项中，根据题意是“和谐集”，又是有限集，故A项为真命题；B项中，设，则，，所以集合是“和谐集”，故B项为真命题；C项中，根据已知条件，可以相等，故任意“和谐集”中一定含有0，所以，故C项为真命题；D项中，取，，都是“和谐集”，但5不属于，也不属于，所以不是实数集，故D项为假命题.故选：D.二、选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。9．十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用，后来英国数学家哈利用奥特首次使用“<”和“>”符号，并逐步被数学界接受，不等号的引入对不等式的发展影响深远.已知，则下列选项正确的是（    ）A． B． C． D．【答案】BC【解析】对于A,由得:，故错误；对于B，因为，所以，故正确；对于C;由得:，故正确；对于D,由于，故，故错误；故选：BC10．在下列四个命题中，正确的是（    ）A．命题“，使得”的否定是“，都有”B．当时，的最小值是5C．若不等式的解集为，则D．“”是“”的充要条件【答案】ABC【解析】对于A，命题“，使得”的否定是“，都有”故A正确；对于B，当时，，当且仅当，即时，等号成立，故B正确；对于C，由不等式的解集为，可知，∴，故C正确；对于D，由“”可推出“”，由，可得或，推不出“”，故D错误.故答案为：ABC.11．设集合，，则下列选项中，满足的实数a的取值范围可以是（　　）A．{a|0≤a≤6} B．{a|a≤2或a≥4}C．{a|a≤0} D．{a|a≥8}【答案】CD【解析】∵集合，满足，∴或，解得或．∴实数a的取值范围可以是{a|a≤0}或{a|a≥8}．故选：CD．12．把定义域为且同时满足以下两个条件的函数称为“函数”：（1）对任意的，总有；（2）若，则有成立.下列说法错误的是（    ）A．若为“函数”，则B．若为“函数”，则一定是增函数C．函数在上是“函数”D．函数在上是“函数”（表示不大于x的最大整数）【答案】BC【解析】对于A，若函数为“函数”，则由条件（1）得.由条件（2），得当时，，所以，故A说法正确；对于B，若，，则满足条件（1）（2），但不是增函数，故B说法错误；对于C，当，时，，，，，不满足条件（2），所以不是“函数”，故C说法错误；对于D，在上的最小值是0，显然符合条件（1）.设上的每一个数均由整数部分和小数部分构成，设x的整数部分是m，小数部分是n，即，则.设y的整数部分是a，小数部分是b，即，则.当时，，当时，，所以，所以函数满足条件（2），所以在上是“函数”，故D说法正确.故选：BC.第Ⅱ卷三、填空题：本题共4小题，每小题5分，共20分。13．已知函数，则___________.【答案】9【解析】根据题意，故答案为：914．已知关于的不等式的解集为或，则关于不等式的解集为_________.【答案】【解析】由关于的不等式的解集为或，可知，且和是方程的两根，故由根与系数的关系得，，又故关于不等式等价为，即，即，解得，故答案为：15．某社团有若干名社员，他们至少参加了A，B，C三项活动中的一项．得知参加A活动的有51人，参加B活动的有60人，参加C活动的有50人，数据如图，则图中__________；__________；__________．【答案】     9     8     10【解析】由题意得，解得.故答案为：①9；②8；③10.16．设函数在区间上的最大值为M，最小值为N，则的值为______.【答案】1【解析】由题意知，（），设，则，因为，所以为奇函数，在区间上的最大值与最小值的和为0，故，所以.故答案为：1四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步棸。17．（10分）已知集合为全体实数集，或，.(1)若，求;(2)若，求实数a的取值范围.【解析】（1）当时，，所以或，又或，所以或；（2）由题可得，当时，则 ，即时，此时满足，②当时，则，所以，综上，实数的取值范围为.18．（12分）已知函数的解析式.(1)求；(2)若，求a的值；(3)画出的图象，并写出函数的值域（直接写出结果即可）.【解析】（1）∵函数的解析式，∴，.（2）∵，，∴或或，解得或.（3）画出函数的图象如图所示：    由图可知，的最大值为，函数的值域为.19．（12分）已知是奇函数，且.(1)求实数的值．(2)判断函数在上的单调性，并加以证明．(3)求的最大值．【解析】（1）是奇函数，．，，，又，解得：.所以.（2）在上为减函数，证明如下：由（1）知，令，则的单调性和的单调性相反，设，则，，，，，即，在上为增函数，则在上为减函数；（3）由（1）（2）结合计算可知：在上递减，在上递增，在上递增，在上递减．又当时，，且，．20．（12分）如图，长方形表示一张（单位：分米）的工艺木板，其四周有边框（图中阴影部分），中间为薄板.木板上一瑕疵（记为点P）到外边框的距离分别为1分米，2分米.现欲经过点P锯掉一块三角形废料，其中M，N分别在上.设的长分别为m分米，n分米.(1)求的值；(2)为使剩下木板的面积最大，试确定m，n的值；(3)求剩下木板的外边框长度（的长度之和）的最大值及取得最大值时m，n的值.【解析】（1）过点分别作的垂线，垂足分别为，则，所以，则，整理可得； （2）要使剩下木板的面积最大，即要锯掉的三角形废料的面积最小，因为，则，可得，当且仅当，即时，等号成立，所以当时，剩下木板的面积最大；（3）要使剩下木板的外边框长度最大，则锯掉的边框长度最小，则，当且仅当，即时等号成立，故此时剩下木板的外边框长度的最大值为分米，此时.21．（12分）（1）若不等式对一切实数x恒成立，求实数a的取值范围；（2）解关于x的不等式．【解析】（1）由题意，恒成立，当时，不等式可化为，不满足题意；       当时，满足，即，解得；       （2）不等式等价于．当时，不等式可化为，所以不等式的解集为；当时，不等式可化为，此时，所以不等式的解集为；     当时，不等式可化为，①当时，，不等式的解集为；②当时，，不等式的解集为或；③当时，，不等式的解集为.22．（12分）已知，函数．(1)当，请直接写出函数的单调递增区间和最小值（不需要证明）；(2)记在区间上的最小值为，求的表达式；(3)对（2）中的，当，恒有成立，求实数的取值范围．【解析】(1)当时，，即，则，故函数的递增区间为，递减区间为，.(2)由题可知，当时，在上递减，在递增，则；当时，在上递减，则，综上：．(3)令，只需，当，且时，，在上单调递减，∴，当时，，在上单调递增，∴；当时，，在上递减，∴，综上可知，，所以．