河南省睢县2022-2023学年九年级（上）数学期末模拟测试(解析版)

这是一份河南省睢县2022-2023学年九年级（上）数学期末模拟测试(解析版)，共22页。试卷主要包含了选择题等内容，欢迎下载使用。
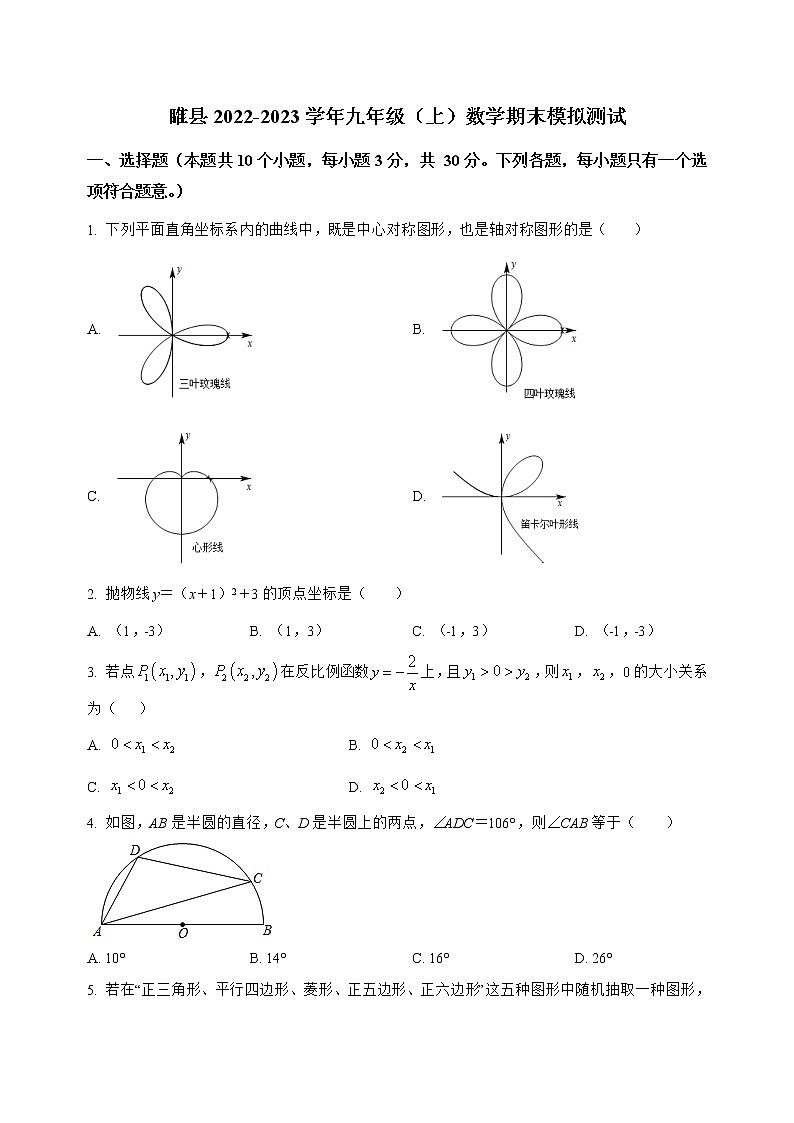
睢县2022-2023学年九年级（上）数学期末模拟测试一、选择题（本题共10个小题，每小题3分，共 30分。下列各题，每小题只有一个选项符合题意。）1. 下列平面直角坐标系内的曲线中，既是中心对称图形，也是轴对称图形的是（    ）A.  B.  C.  D. 2. 抛物线y＝（x＋1）2＋3的顶点坐标是（    ）A. （1，﹣3） B. （1，3） C. （﹣1，3） D. （﹣1，﹣3）3. 若点，在反比例函数上，且，则，，的大小关系为（   ）A.  B.  C.  D. 4. 如图，AB是半圆的直径，C、D是半圆上的两点，∠ADC＝106°，则∠CAB等于（　　）A. 10° B. 14° C. 16° D. 26°5. 若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率是(　 　)A.  B.  C.  D. 6. 不透明的袋子中装有红球1个、绿球1个、白球2个，除颜色外无其他差别．随机摸出一个小球后不放回，再摸出一个球，则两次都摸到白球的概率是（　　）A.  B.  C.  D. 7. 已知反比例函数y＝，下列结论不正确的是（　　）A. 图象经过点（1，1）B. 图象在第一、三象限C. 当x＞1时，0＜y＜1D. 当x＜0时，y随着x的增大而增大8. 如图，在中，点在边上，若，，且，则线段的长为（    ）A. 2 B.  C. 3 D. 9. 如图，点A，B在反比例函数y＝（k＜0）的图象上，AD⊥x轴于点D，BE⊥x轴于点E，BC⊥y轴于点C、连结AC．若OC＝1，OD＝OE，AC＝AD，则k的值为（　　）A. ﹣2 B. ﹣ C. ﹣4 D. ﹣10. 如图，在Rt△ABC中，∠C＝90°，∠A＝60°，AB＝8，点P是AB边上直面的一个动点，过点P作PD⊥AB交直角边于点D，设AP为x，△APD的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（    ）A.                     B.  C.  D. 二.填空题(共5题，总计 15分)11. 与点关于原点中心对称的点的坐标为__．12. 一个不透明袋子中装有四个小球，它们除了分别标有的数字1，2，3，6不同外，其他完全相同，任意从袋子中摸出一球后不放回，再任意摸出一球，则两次摸出的球所标数字之积为6的概率是__________．13. 教练对小明推铅球的录像进行技术分析，如图，发现铅球行进高度与水平距离之间的关系为 ，由此可知铅球推出的距离_____ ．14. 如图，⊙O与△OAB的边AB相切、切点为B．将△OAB绕点B按顺时针方向旋转得到△O'A'B，使点O落在⊙O上，边A'B交线段AO于点C．若∠A'＝27°，则∠OCB＝_____度．15. 在一张边长为2的等边△ABC的纸片上做折纸游戏，其中点D是AC的中点，如图（1），在AB边上任取一点E，将纸片沿DE折叠，使点A落在处，再将纸片沿折叠，点E落在处，如图（2）；当点恰好落在原等边三角形纸片的边上（不与顶点重合）时，线段AE的长为___．三.解答题(共8题，总计75分)16. 小明与小亮两位同学解方程的过程如下框：小明：两边同除以，得．则．小亮：移项，得．提取公因式，得则或．解得，．任务一：你认为他们的解法是否正确？若正确请在括号内打 “√”；若错误请在括号内打“×”；小明 　   　，小亮 　   　；任务二：写出你的解答过程．17. 如图，在平面直角坐标系中，三个顶点的坐标分别是A（2，4），B（1，2），C（5，3）．（1）作出关于点O对称的图形；（2）以点O为旋转中心，将顺时针旋转90°，得到，在坐标系中画出．18. 如图，聪聪想在自己家的窗口A处测量对面建筑物CD的高度，他首先量出窗口A到地面的距离（AB）为16m，又测得从A处看建筑物底部C的俯角α为30°，看建筑物顶部D的仰角β为53°，且AB，CD都与地面垂直，点A，B，C，D在同一平面内．（1）求AB与CD之间的距离（结果保留根号）．（2）求建筑物CD的高度（结果精确到1m）．（参考数据：，，，）19. 如图，在Rt中，，以AB为直径作，点D为上一点，且，连接DO并延长交CB的延长线于点E．（1）求证：CD是的切线：（2）若，，求AC的长．20. 某超市经销一种商品，每千克成本为元，经试销发现，该种商品的每天销售量（千克）与销售单价（元 / 千克）满足一次函数关系，其每天销售单价，销售量的四组对 应值如下表所示：销售单价（元 / 千克）销售量（千克）（1）求（千克）与（元/千克）之间的函数表达式；（2）当物价部门规定销售利润不得高于问销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？（3）为保证某天获得销售利润不低于元，则该天的销售量最多为多少？21. 如图，已知直线与双曲线交于A（a，2），B（－2，b）两点，过点A作AC⊥x轴于点C． （1）A点的坐标为___，B点的坐标为___，双曲线解析式为___．（2）若点P在直线y＝x＋1上，是否存在点P，使若存在，请求出此时点P的坐标，若不存在，请说明理由．22. 如图，抛物线y＝x2+bx+c与x轴交于A，B两点，与y轴交于C点，顶点为D，点E为线段BD上一个动点，EF⊥x轴，垂足为点F，OB=OC=3．（1）求抛物线的解析式；（2）当∠CEF＝∠ABD时，补全图形并求点E的坐标．23. 边长为4的正方形ABCD绕顶点A，按顺时针方向旋转至正方形，记旋转角为．（1）如图1，当时，求弧的长度和线段AC扫过的扇形面积；（2）如图2，当时，记BC与的交点为E，求线段的长度；（3）如图3，在旋转过程中，若F为线段的中点，求线段DF长度的取值范围．
睢县2022-2023学年九年级（上）数学期末模拟测试参考答案及解析一.选择题 1.【答案】：B【解析】：解：A、是轴对称图形，但不是中心对称图形，故不符合题意；B、既是轴对称图形也是中心对称图形，故符合题意；C、是轴对称图形，但不是中心对称图形，故不符合题意；D、是轴对称图形，但不是中心对称图形，故不符合题意；故选B．2.【答案】：C【解析】：解：抛物线y＝2（x＋1）2＋3的顶点坐标是（﹣1，3）．故选：C．2.【答案】：C【解析】：解：∵   ，∴   图象在二四象限，∵   ，∴   .故选.4.【答案】：C【解析】：解：连接BD，如图，∵AB是半圆的直径，∴∠ADB＝90°，∴∠BDC＝∠ADC﹣∠ADB＝106°﹣90°＝16°，∴∠CAB＝∠BDC＝16°．故选：C．5.【答案】：C【解析】：这五种图形中，平行四边形、菱形和正六边形是中心对称图形，所以这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率=．故选C6.【答案】：B【解析】：画树状图为：

共有12种等可能的结果数，其中两次摸出的球都是的白色的共有2 种，
所以两次都摸到白球的概率是.故选B．7.【答案】：D【解析】：解：A、当x＝1时，y＝＝1，∴图象经过点（1，1），正确；B、∵k＝1＞0，∴图象在第一、三象限，正确；C、∵k＝1＞0，图象经过点（1，1）∴图象在第一象限内y随x的增大而减小，∴当x＞1时，0＜y＜1，正确；D、∵k＝1＞0，∴当x＜0时，y随着x的增大而减小，原说法错误；故选：D．8.【答案】：B【解析】：解：∵∠BCD＝∠A，∠B＝∠B，
∴△BCD∽△BAC，
∴，∵BC＝3，BD＝2，
∴，
∴BA＝，
∴AD＝BA−BD＝−2＝．
故选：B．9.【答案】：D【解析】：解：∵AD⊥x轴于点D，BE⊥x轴于点E，∴四边形BEOC是矩形，∴BE＝OC＝1，把y＝1代入，求得x＝k，∴B（k，1），∴OE＝﹣k，∵OD＝OE，∴OD＝k，∵BC⊥y轴于点C，把x＝k代入得，y＝，∴AC＝AD＝，∵OD＝CF＝-k，AF＝﹣1＝，在Rt△ACF中，AC2＝CF2+AF2，∴，解得k＝±，∵k<0，∴k＝﹣，故选：D．10.【答案】：B【解析】：解：，，，，，当点在上时，；当点在上时，如图所示，，，，又∵，，，该函数图象前半部分是抛物线开口向上，后半部分为抛物线开口向下．故选：B．二. 填空题11.【答案】： 【解析】：根据中心对称的性质，点P（2，﹣4）关于原点中心对称的点的坐标为（﹣2，4）．故答案为：（﹣2，4）．12.【答案】：【解析】：解：列表如下：所有等可能的情况有12种，其中两次摸出的球所标数字之积为6的有4种结果，
所以两次摸出的球所标数字之积为6的概率为.故答案为：.13.【答案】：10【解析】：解：令函数式中，y=0，0=，解得x1=10，x2=-2（舍去），即铅球推出的距离是10m．故答案为：10．14.【答案】： 87【解析】：解：连接OO'，∵⊙O与△OAB的边AB相切，∴AB⊥OB，由旋转的性质可知，∠O'BA'＝∠OBA＝90°，BO＝BO'，∵OB＝OO'，∴OB＝O'B＝OO'，∴△OBO'为等边三角形，∴∠OBO'＝60°，∴∠ABC＝60°，∴∠OCB＝∠A+∠ABC＝27°+60°＝87°，故答案为：87．15.【答案】： 或【解析】：解：分两种情况求解：①如图（1）落在边上时，与的交点为由题意知，，，∴，∴，∵∴解得；②如图（2），落在边上时，与的交点为，过点E作由题意知，，，∴∴，，∵∴解得∴∴；故答案为：或．【点睛】本题考查了翻折的性质，等边三角形的性质，含30°的直角三角形，等腰直角三角形，三角函数值等知识．解题的关键在于分情况求解．三.解答题16【答案】：任务一：×，×；任务二：见解析．【解析】：解：任务一：∵小明忽略的情况， ∴小明×，∵小亮提取公因式时添加括号没有变号，∴小亮×，故答案为：×，×；任务二：移项，得．提取公因式，得．则或．解得，．17【答案】：（1）见解析；（2）见解析【解析】：1）如图所示，即所求．（2）如图所示，即为所求．18【答案】：（1）；（2）51m【解析】：解：（1）作于M，则四边形ABCM为矩形，，，在中，，则，答：AB与CD之间的距离；（2）在中，，则，，答：建筑物CD的高度约为51m．19【答案】：（1）证明见解析    （2）【解析】：【小问1详解】证明：连接OC．∵CB=CD，CO=CO，OB=OD，∴△OCB≌△OCD（SSS），∴∠ODC=∠OBC=90°，∴OD⊥DC，∴DC是⊙O的切线；【小问2详解】设⊙O的半径为r．在Rt△OBE中，∵OE2=EB2+OB2，∴（4-r）2=r2+22，∴r=1.5．∵，∴，∴CD=BC=3，在Rt△ABC中，．∴AC的长为．20【答案】：（1）y与x之间的函数表达式为y=-2x+180；（2）当销售单价定为65元/千克时，才能使当天的销售利润最大，最大利润是750元；（3）销售为60千克．【解析】：解：（1）设y与x之间的函数表达式为y=kx+b（k≠0），将表中数据（55，70）、（60，60）代入得：，解得：．∴y与x之间的函数表达式为y=-2x+180．（2）设当天的销售利润为w元，则：w=（x-50）（-2x+180），∵销售利润不得高于，∴ ∴ ∵-2＜0，∴当x=70时，w最大值=800．当时，y的值随x的增大而增大，∴当x=65时，当天的销售利润有最大值，最大值等于：（元）所以，当销售单价定为65元/千克时，才能使当天的销售利润最大，最大利润是750元；答：当销售单价定为65元/千克时，才能使当天的销售利润最大，最大利润是750元．（3）由题意得：（x-50）（-2x+180）=600，整理得：x2-140x+4800=0，解得x1=60，x2=80．∴为保证某天获得销售利润不低于600元利润，x范围为：
 由（1）y=-2x+180，∴当x=60时，销售量最大为60千克答：为保证某天获得销售利润不低于600元，则该天的销售量最多为60千克．【点睛】本题考查了待定系数法求一次函数的解析式、一元二次方程和二次函数在实际问题中的应用，理清题中的数量关系是解题的关键．21【答案】：（1）A(1，2)，B(−2，−1)，    （2）存在，(3，4)或(−1，0)【解析】：【小问1详解】∵A、B两点在直线y＝x＋1上∴a+1=2，−2+1=b∴a=1，b=−1即A、B两点的坐标分别为(1，2)、(−2，−1)∵A(1，2)在双曲线上∴∴k=2∴双曲线解析式为故答案为：A(1，2)，B(−2，−1)，【小问2详解】存在由题意，设点P的坐标为(m，m+1)，则点P到AC的距离为∵A(1，2)，且AC⊥x轴∴AC=2，OC=1∴， ∵∴ 解得：m=3或m=−1则m+1=4或0∴P点的坐标为(3，4)或(−1，0)22【答案】：（1）y＝x2−2x−3；    （2）作图见解析，E（，−）．【解析】：【小问1详解】解：∵OB＝OC＝3，∴B（3，0），C（0，−3），将B（3，0），C（0，−3）代入y＝x2＋bx＋c得：，解得，∴抛物线的解析式为y＝x2−2x−3；【小问2详解】如图：过D作DG⊥x轴于G，过C作CH⊥EF于H，∵y＝x2−2x−3＝（x−1）2−4，∴抛物线顶点D（1，−4），∴OG＝1，DG＝4，∵B（3，0），∴BG＝OB−OG＝2，∴tan∠ABD＝，设直线BD解析式是y＝kx＋b，代入B、D两点坐标，∴，解得，∴直线BD解析式是y＝2x−6，设E（t，2t−6），则CH＝xE＝t，EH＝yC−yE＝−3−（2t−6）＝3−2t，∴tan∠CEF＝，∵∠CEF＝∠ABD，∴，解得t＝，∴2t−6＝2×−6＝−，∴E（，−）．23【答案】：（1）弧的长度，扇形的面积；（2）；（3）DF的取值范围为．【解析】：（1）∵四边形ABCD是正方形，∴，，∴，∵，∴的长度，扇形的面积；（2）如图2，连接，∵旋转角，∴，∴点B在对角线上，在中，，∴，∵，，∴是等腰直角三角形，∴，∴；（3）如图3，连接，取中点，则，又∵∴，，∴点F的轨迹是以О为圆心、2为半径的圆，∵，∴，∴，∴DF的取值范围为．