数学必修 第二册第六章 平面向量及其应用6.4 平面向量的应用完美版课件ppt

课题名

正弦定理、余弦定理应用举例

教学目标

1.知识与技能:用正、余弦定理解决实际问题中的三角形；

2.过程与方法:实际问题转化为数学问题建模计算所求的量。

3.情感态度和价值观: 培养学生实际与理论相互转化的能力，提升应用与逻辑推理的能力。  

教学重点

利用正弦定理、余弦定理解决实际生活中的三角形相关问题。

教学难点

准确建模，灵活应用正、余弦定理解决实际问题中的三角形相关问题。

一、 新课导入

（一）   教师活动:

怎样把现实生活中的三角形问题通过建模转化为数学中的三角形问题呢？请看……

学生活动

 回忆正、余弦定理的有关知识，结合实际生活中的三角形特征，积极思考猜想怎么解决生活中的角和线段的长度问题。

（二）   设计意图

学以致用是我们的宗旨和目的，为了解决生活中的三角形问题，必须学会建模，联系正、余弦定理解决此类问题。

新知讲授

（一）   教师活动

1.温故知新：

(1)余弦定理的数学表达式：       

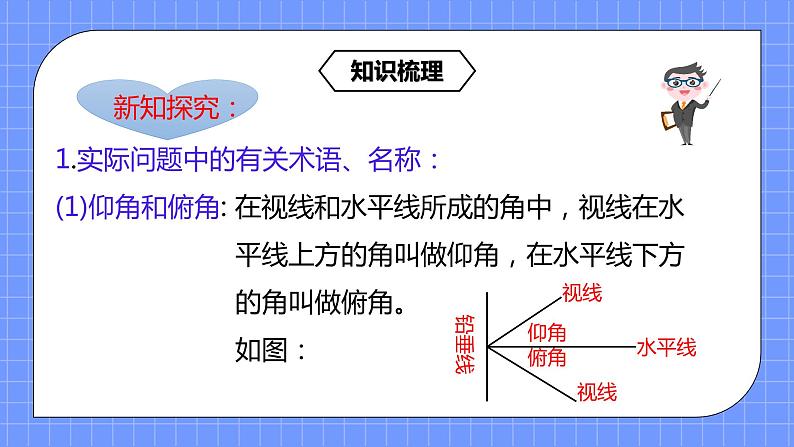
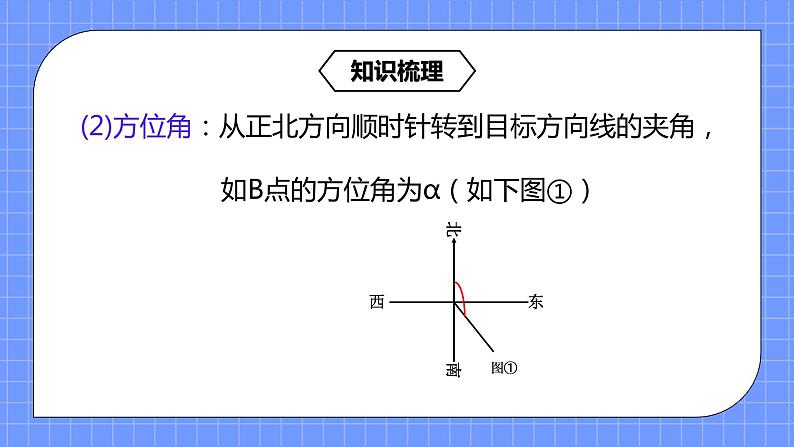
(2)公式变形：          

其中

(3)正弦定理的数学表达式：= ,其中R为外接圆的半径。

(4)公式变形：

2.新知探究：

(1)实际问题中的有关术语、名称：                   

①仰角和俯角: 在视线和水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角。

  ②方位角：从正北方向顺时针转到目标方向线的夹角。

  ③方向角:①正南方向：从原点O出发的经过目标射线与正南的方向线重合，即目标在正南的方向线上.依次可推正北方向、正东方向和正西方向.

②东南方向：指经过目标的涉嫌是正东和正南的夹角平分线。

③北偏东α：从正北向正东方向旋转α角度。

④南偏西β：从正南向正西方向旋转β角度。

(2)解题基本思路：

 实际问题         数学问题           解数学问题         回到实际问题

学生活动

1. 新知探究：

(1)    实际问题中的有关术语、名称：

①     仰角和俯角:  

                                   仰角

                                                      水平线

                                       俯角

②     方位角：          北

                              方位角

                                          东

③     方向角：

设计意图

激发学生积极思考的潜意识，检验学生课前预习的能力。

提出问题，共同解答问题中的要点及疑惑.

二、 知识巩固

1. 跟踪练习：

(1)设A,B两点在河的两岸，测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50m ,  ，后，计算，两点间的距离为(      )m

    A.        B.      C.D.

解析：如图，由正弦定理得

      ∴    故，两点的距离为.         故选A.

答案：A.

(2)灯塔A,B与海洋观察站C的距离都等于a(km), 灯塔A在 C北偏东30°,B在C南偏东60°,则A,B之间的相距是(      )

解析：由题意得，

      所以.         故选A.

答案：A.

(3)如图所示，为测一树的高度，在地面上选取两点，从两点分别测得树尖的仰角为30°，45°且两点之间的距离为，则树的高度为（        )m

   A.    B.    C. D.

解析:在中，     

所以

     由正弦定理得:

     所以树的高度为(m).   故选A.

答案：A.     

课堂互动：

(1)如图，在山脚测得山顶的仰角为，沿倾斜角为斜坡向上走米到，在处测得山顶的仰角为则山高(              )米.

    A.         B.         C.        D.

解析: 设   ,

      在中，

 ，

      ∴           ∴．

  故选A       

答案：A.

(2)当太阳光与水平面的倾斜角为60°时，一根长为的竹竿如图所示装置，要使它的影子最长，则竹竿与地面所成的角是（        ).

       A.      B.         C.  D.

解析:设竹竿与地面所成的角是， 影子长为，由正弦定理得

             所以

      ，     当

      即时，取得最大值，

      竹竿与地面所成的角为时，影子最长为米，   故选B.

答案：B.       

(3)海上有两个小岛相距10 海里，从岛望岛和 岛成60°的视角，从岛望岛和岛成75°的视角，则间的距离是（     ）海里。

    A.             B.          C.          D.

解析：根据题意,可得如图.在中,  ,   ,

      由正弦定理可得

      即       ∴ (海里)     故选D.

答案：D.         

(4)如图所示，为了测量某一隧道两侧两地间的距离，某同学首先选定了不在直线上的一点（， 所对的边分别为然后确定测量方案并测出相关数据，进行计算．现给出如下四种测量方案； 

①     测量；  ②测量；  ③测量； 

 ④测量，则一定能确定间距离的所有方案的序号为(     ）

  A.①③       B.①③④       C.②③④      D.①②④   

解析：对①：由，可求得，再由 ，求得

      对②：由三个角无法确定三角形，故无法计算的值；

对③：由，即可求得的值；

对④：由可求得，再由，即可求得的值.

综上所述：①③④可以求得.          故选B.

答案：B.    

3.素养训练：

(1)如图，两点为山脚下两处水平地面上的观测点，在两处观察点观察山顶点的仰角分别为， 若， ，且观察点之间的距离比山的高度多200米，则山的高度为(　　      )米。

      A.200      B.110     C.120     D.130

 解析: 设山的高度为x米，如图所示：由  , 

在直角 中，可得     

      又

      即

答案：A.          

(2)如图，某人在点处测得某塔在南偏西的方向上，塔顶仰角为，此人沿正南方向前进30米到达 处，测得塔顶的仰角为，则塔高为(          )米。

     A.20           B.15           C. 12         D.10

解析：设塔底为，塔高为h米，故，         由于米       在三角形中,由余弦定理得

          解得米.    故选B.

答案：B.        

课堂小结

1. 实际问题中的有关术语、名称：

（1）仰角与俯角 ；      （2）方位角；        （3）方向角。

2.解题思路：

拓展提升:

1.一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进100 m到达点B，在B点测得水柱顶端的仰角为30°，则水柱的高度是(　　)m.

A．50          B．100         C．120      D．150

解析：如图所示，设水柱CD的高度为h．在Rt△ACD中，∵∠DAC=45°，

∴AC=h．   ∵∠BAE=30°，∴∠CAB=60°．

又∵B，A，C在同一水平面上，

∴△BCD是以C为直角顶点的直角三角形，

在Rt△BCD中，∠CBD=30°，∴BC=．

在△ABC中，由余弦定理可得：BC2=AC2+AB2﹣2AC•ABcos60°．

∴（）2=h2+1002﹣，   化为h2+50h﹣5000=0，

解得h=50．   故选A．

答案：A.

布置作业

课本P51.      练习：       1、2、3.

课本P53.      习题6.4：    12、13、14. 

板书设计

1.仰角与俯角：                                 3.

2.方位角与方向角：                             4.                                   

跟踪练习：1.                                 素养训练：1.

          2.                                           2.

          3.                                          

课堂互动：1.                                 拓展提升：1..

          2.

教学反思

准确的将各个实际问题转化为数学问题并建模进行解答是值得加强训练的。