高中数学人教A版 (2019)必修 第一册2.1 等式性质与不等式性质课后练习题

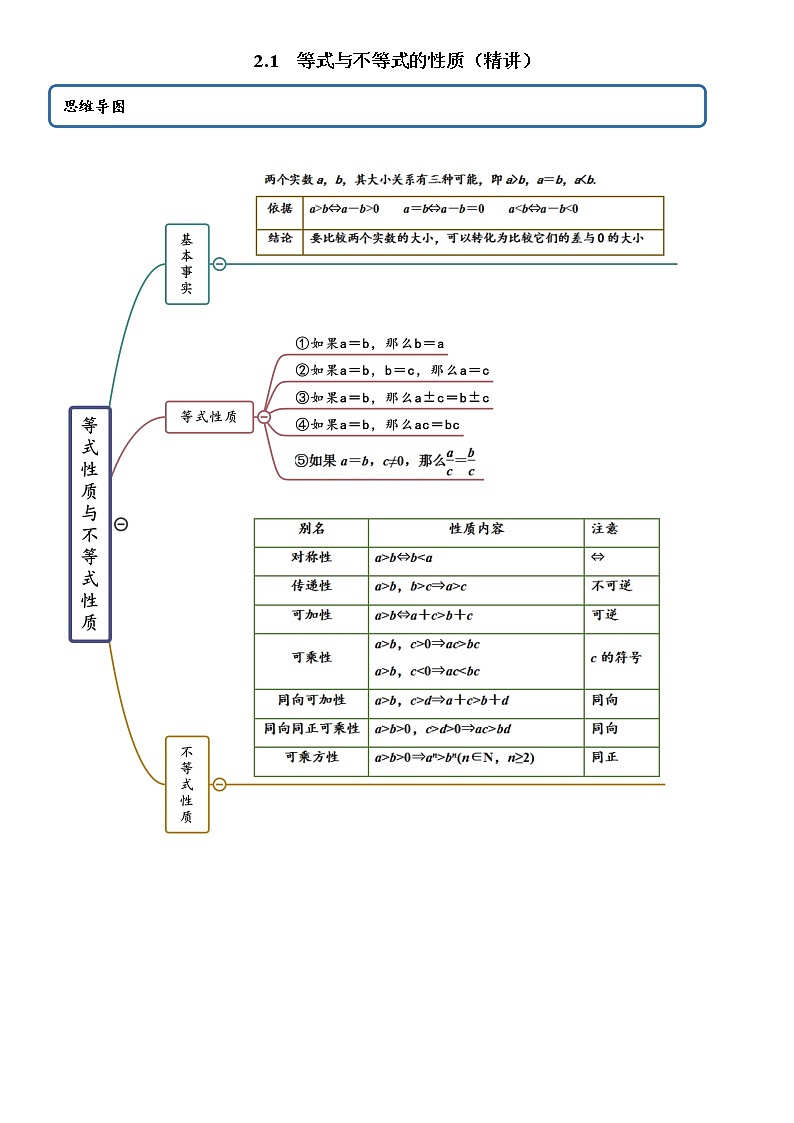
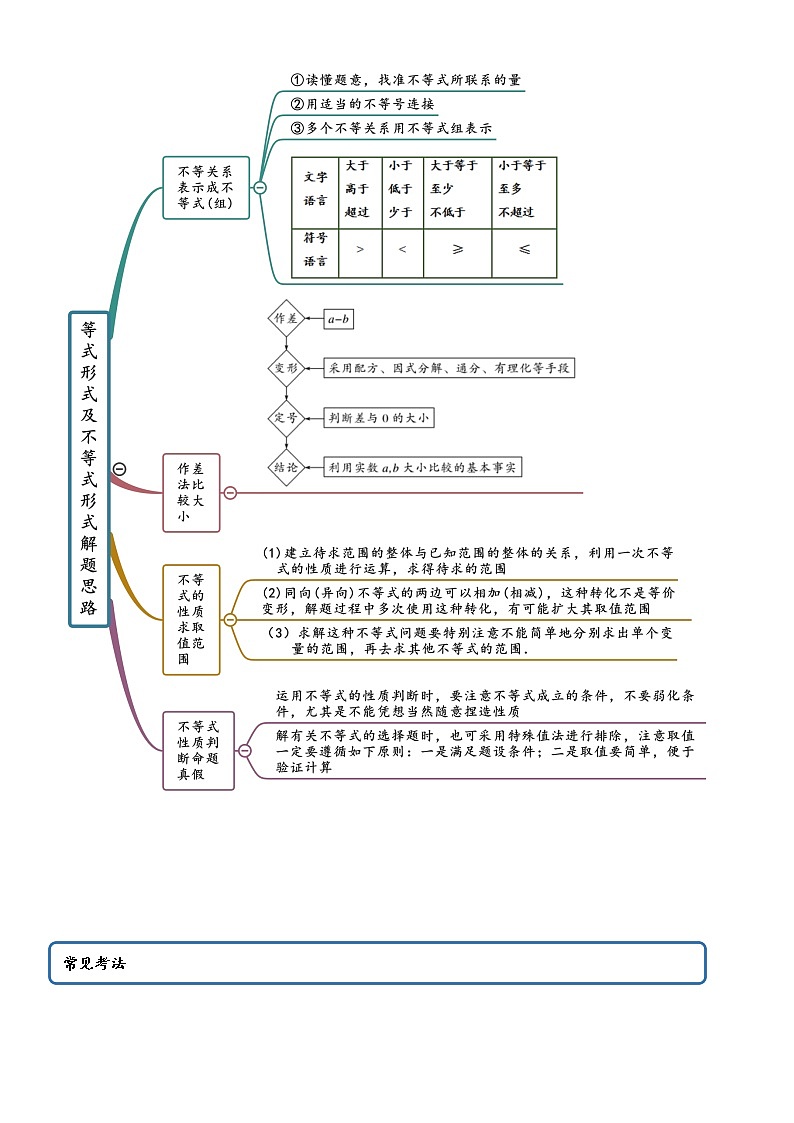
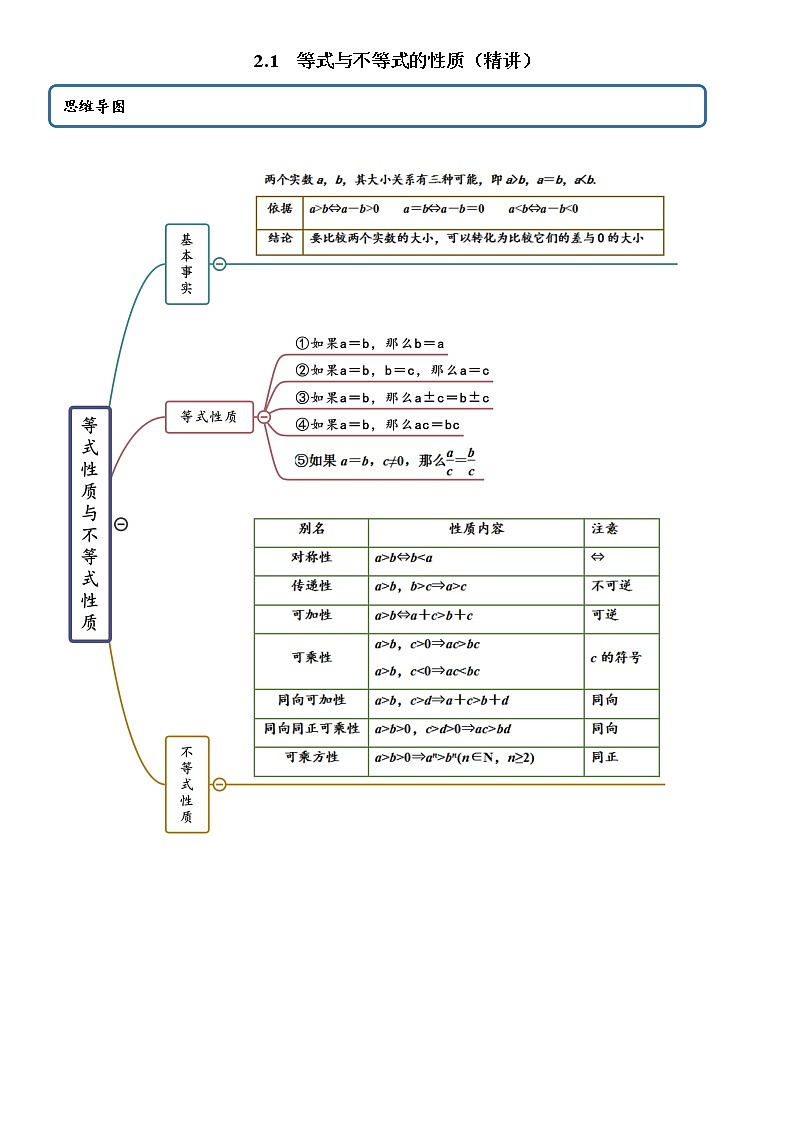
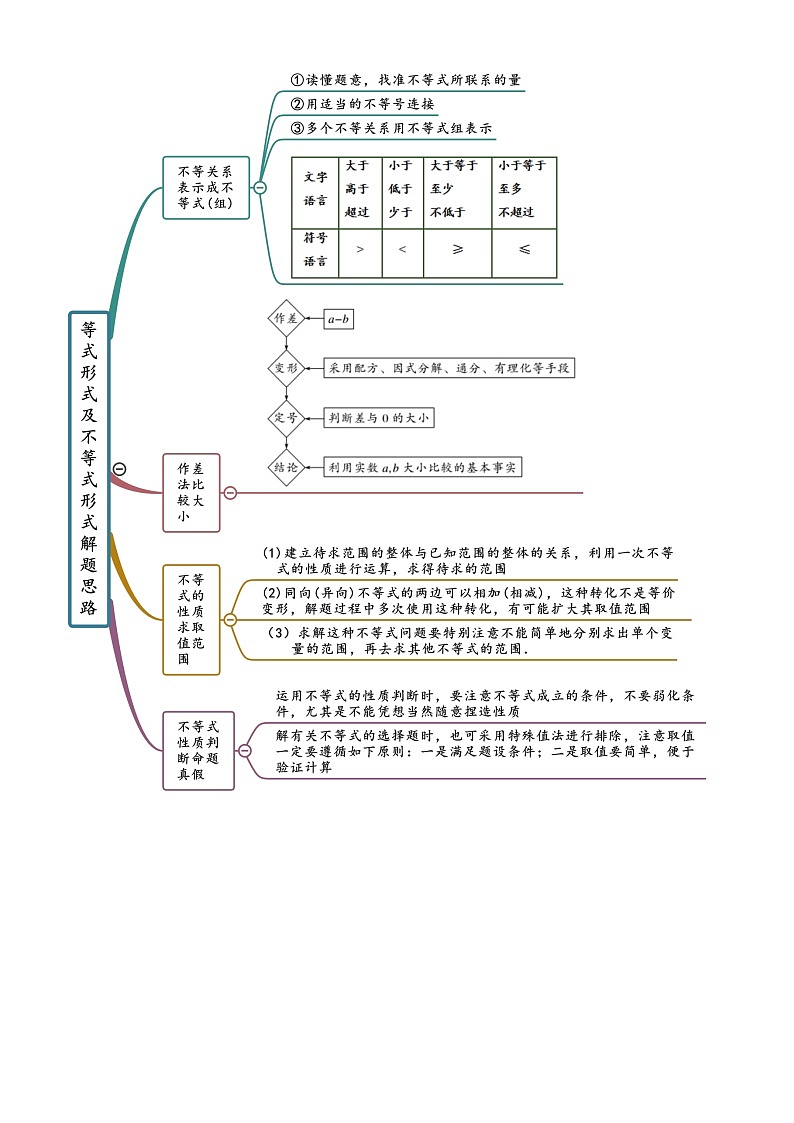
2.1  等式与不等式的性质（精讲）

考点一 不等式（组）表示实际问题

【例1】（2021·山东潍坊市）铁路总公司关于乘车行李规定如下：乘坐动车组列车携带品的外部尺寸长、宽、高之和不超过．设携带品外部尺寸长、宽、高分别为（单位：），这个规定用数学关系式表示为（    ）．

A． B．

C． D．

【答案】C

【一隅三反】

1．（2021·安庆市）某高速公路要求行驶的车辆的速度的最大值为，同一车道上的车间距不得小于，用不等式表示为（    ）

A．且 B．或

C． D．

【答案】A

2．（2021·安徽芜湖市）我国经典数学名著《九章算术》中有这样的一道题：今有出钱五百七十六，买竹七十八，欲其大小率之，向各几何？其意是：今有人出钱576，买竹子78根，拟分大､小两种竹子为单位进行计算，每根大竹子比小竹子贵1钱，问买大､小竹子各多少根？每根竹子单价各是多少钱？则在这个问题中大竹子每根的单价可能为（    ）

A．6钱 B．7钱 C．8钱 D．9钱

【解】依题意可设买大竹子，每根单价为，购买小竹子，每根单价为，

所以，即，即，

因为，所以，

根据选项，，所以买大竹子根，每根元.故选：C

考点二 比较大小

【例2-1】（2021·安徽六安市·六安一中高一开学考试）已知，，则、 的大小关系为（    ）

A． B． C． D．无法确定

【答案】C

【例2-2】（2021·黑龙江鹤岗市）设，比较与的大小

【答案】

【一隅三反】

1．（2021·海南省农垦加来高级中学高一期末）比较与的大小（    ）

A．无法比较大小 B．

C． D．

【答案】B

2．（2021·平潭县新世纪学校）已知， ，则 和的大小关系为（    ）

A． B．

C． D．

【答案】D

3．（2021·上海），比较与的大小．

【答案】

考点三  不等式性质的运用

【例3】（2021·四川）若，则下列不等关系一定正确的是（    ）

A． B． C． D．

【答案】B

【一隅三反】

1．（2021·四川省绵阳南山中学）若，则下列不等式中，不能成立的是（    ）

A． B． C． D．

【答案】B

2．（2021·全国高三）已知a>b，c>d，则下列关系式正确的是（    ）

A．ac+bd>ad+bc B．ac+bd<ad+bc

C．ac>bd D．ac<bd

【答案】A

3．（2021·浙江高一期末）已知，且，那么下列各式中正确的是（    ）

A． B． C． D．

【答案】D

4．（2021·全国高一课时练习）设a<b<0，则下列不等式中不正确的是（    ）

A． B．ac<bc

C．|a|>－b D．

【答案】B

5.（2021·东至县第三中学高一期中）下列结论正确的个数为（    ）

①两个实数，之间，有且只有，，三种关系中的一种；

②若，则；

③一个不等式的两边同加上或同乘以同一个数，不等号方向不变；

④一个非零实数越大，则其倒数就越小；

⑤，；

⑥若，则．

A．2 B．3 C．4 D．5

【答案】B

考点四 不等式的证明

【例4】（2021·平潭县新世纪学校高一月考）（1）已知，求证：；

（2）已知，求证：；

（3）已知，求证：.

证明：（1）因为，所以.则.

（2）因为，所以.又因为，所以，即，因此.

（3）因为，根据（2）的结论，得.

又因为，则 ，即.

【一隅三反】

1．（2021·全国高一课时练习）已知，，，求证：．

【解】，，

又，，，

又，．

2．（2020·上海）设，求证：．

【解】

考点五  求代数式的范围

【例5】（2021·江苏省）已知，，则的取值范围是（    ）

A． B． C． D．

【答案】C

【一隅三反】

1．（202··四川雅安市）已知，，则的取值范围是（    ）.

A． B． C． D．以上都不对

【答案】A

2．（2021·辽宁葫芦岛市）（多选）已知实数满足，则（    ）

A． B．

C． D．

【答案】AC

3．（2021·浙江）（多选）设x，y为实数，满足，，则下列结论正确的是（    ）

A． B． C． D．

【答案】AC