沪教版 (五四制)八年级下册第三节 无理方程备课课件ppt

这是一份沪教版 (五四制)八年级下册第三节 无理方程备课课件ppt，共26页。PPT课件主要包含了整式方程，分式方程，无理方程，代数式，代数方程，有理方程，已知下列关于x的方程，去根号，方程两边平方得，整理得等内容，欢迎下载使用。

所列的方程有什么特点？它与前面所学的方程有什么区别？
已知一个实数x（x＞0）的3倍与4的和的算术平方根等于它本身，求实数x.
方程中含有根式，且被开方数是含有未知数的代数式，这样的方程叫做无理方程。无理方程也叫做根式方程。
辨一辨：下列方程是不是无理方程？若不是，则是什么方程？
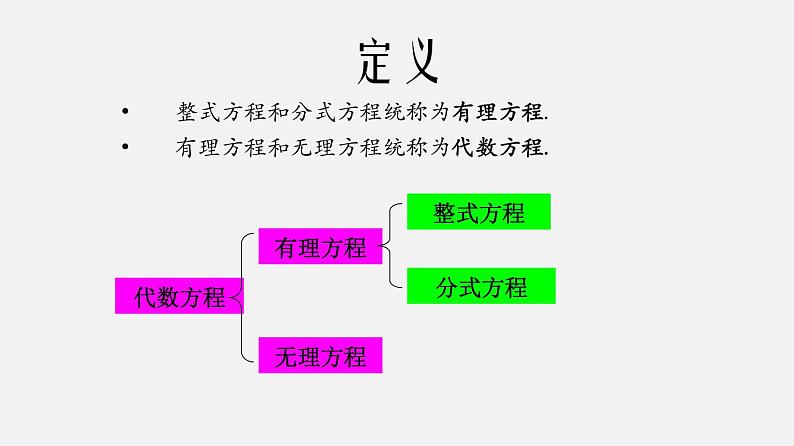
整式方程和分式方程统称为有理方程.有理方程和无理方程统称为代数方程.
其中无理方程是____________________(填序号).
怎样将无理方程转化成有理方程？
方程变形的依据是什么？
它们都是原方程的根吗？
检验：把x=4代入原方程的两边，左边=4，右边=4左边=右边， x=4是原方程的根
把x=-1代入原方程的两边，左边=-1，右边=1左边≠右边， x=-1是原方程的增根，舍去
讨论：为什么会产生增根？
1、解无理方程的一般步骤是什么？
无理方程如何进行“验根”？
代入原方程的左边和右边，使左边=右边，且根号有意义．
增根产生的原因是什么？
平方把无理方程化为有理方程，使原方程中未知数允许取值的范围扩大了．
你能判断这个方程实数根的情况吗?
左边=一个非负数+1>0，右边=0,所以原方程没有实数根．
下列方程中，有实数根的方程是：（ ）
2.下列方程中，有实数根的方程是…………（ ） （A） ； （B） ； （C） ； （D） .
解只含一个“根号”的无理方程时：
将“根号项”放在方程的一边
其它“项”放在方程的另一边
然后进行平方，化为有理方程.
方程中含有根式，且被开方数是含有未知数的代数式，这样的方程叫做无理方程.
将方程化为一般形式 ．
当 x=4时.右边=-2,可知x=4是增根，舍去.当 x=12，右边=左边=6，可知x=12是原方程的根.
经检验:x=4是增根，舍去；x=12是原方程的根．
．所以原方程的根是x=12.
一般将“根号项”放在方程的一边，把其他“项”放在方程的另一边.
可以直接平方去根号吗？
转化为等号一边含根号，等号另一边不含根号.
当 x=6时.左边=0，右边=-3,可知x=6是增根，舍去.当 x=2，右边=左边=1，可知x=2是原方程的根.
经检验x=6，是增根，舍去；x=2是原方程的根．
．所以原方程的根是x=2.
解只含一个“根号”的无理方程时：
两边平方，化为有理方程.
方程两边可以直接平方 ．
当 x=-1时.左边无意义,可知x=-1是增根，舍去.当 x=3，右边=左边，可知x=3是原方程的根.
经检验：x=-1是增根，舍去；x=3是原方程的根．
．所以原方程的根是x=3.
解含有两个“根号”的无理方程时：
通过移项使等号两边各含一个根号再平方较简单.
将方程整理化为只含一个根号 ．
一般将两个“根号项”分别放在等号两边.
第二次平方，把原方程转化为有理方程．