初中数学沪教版 (五四制)八年级下册第一节 多边形备课ppt课件

这是一份初中数学沪教版 (五四制)八年级下册第一节 多边形备课ppt课件，共34页。PPT课件主要包含了温故知新，想一想，探究新知，多边形的外角和，多边形外角和定理等内容，欢迎下载使用。
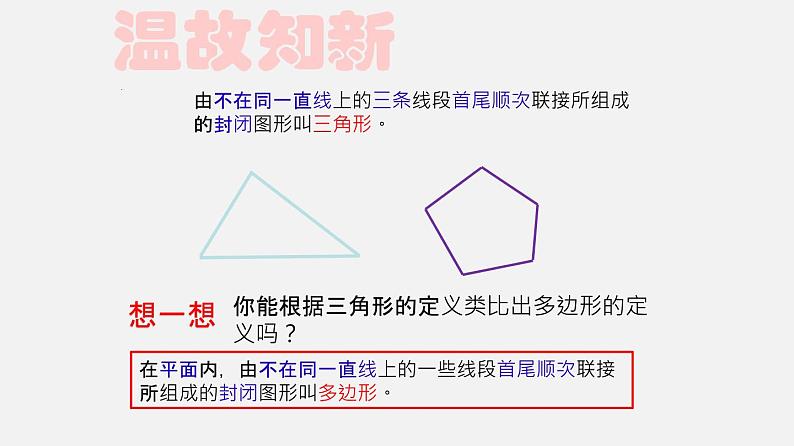
你能根据三角形的定义类比出多边形的定义吗？
由不在同一直线上的三条线段首尾顺次联接所组成的封闭图形叫三角形。
在平面内，由不在同一直线上的一些线段首尾顺次联接所组成的封闭图形叫多边形。
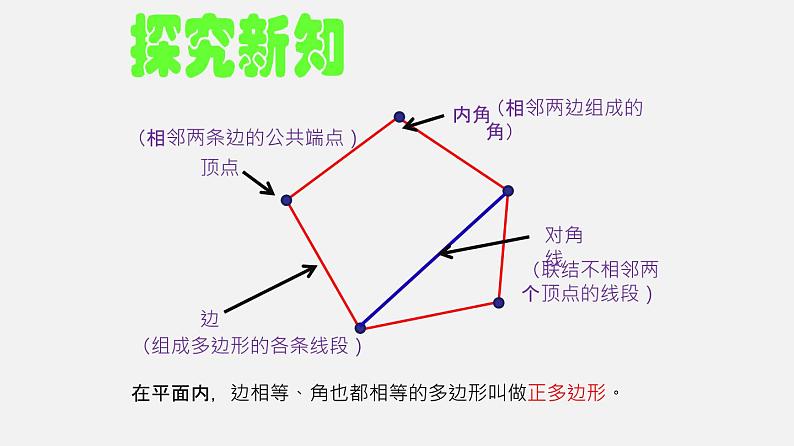
（组成多边形的各条线段）
（相邻两条边的公共端点）
（联结不相邻两个顶点的线段）
在平面内，边相等、角也都相等的多边形叫做正多边形。
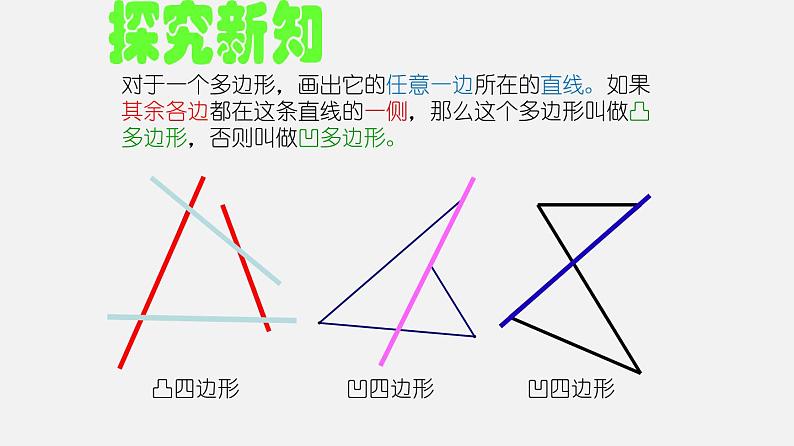
对于一个多边形，画出它的任意一边所在的直线。如果其余各边都在这条直线的一侧，那么这个多边形叫做凸多边形，否则叫做凹多边形。
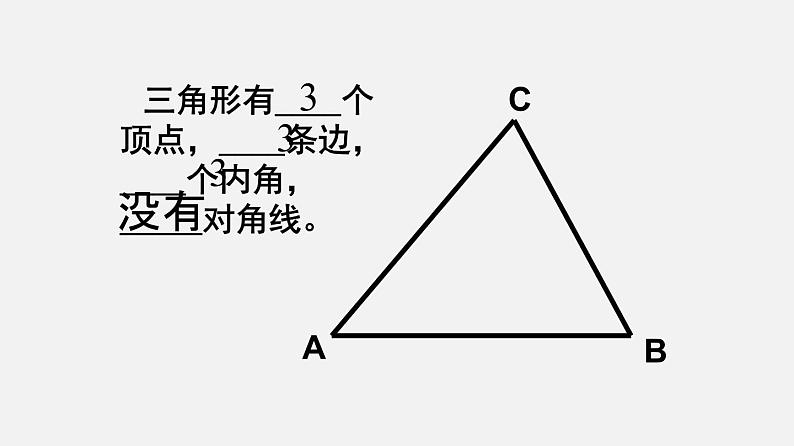
三角形有____个顶点，____条边，____个内角，_____对角线。
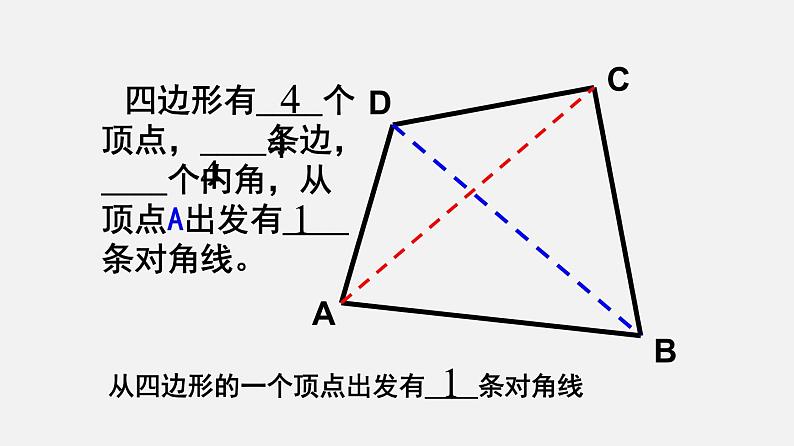
四边形有____个顶点，____条边，____个内角，从顶点A出发有____条对角线。
从四边形的一个顶点出发有____条对角线
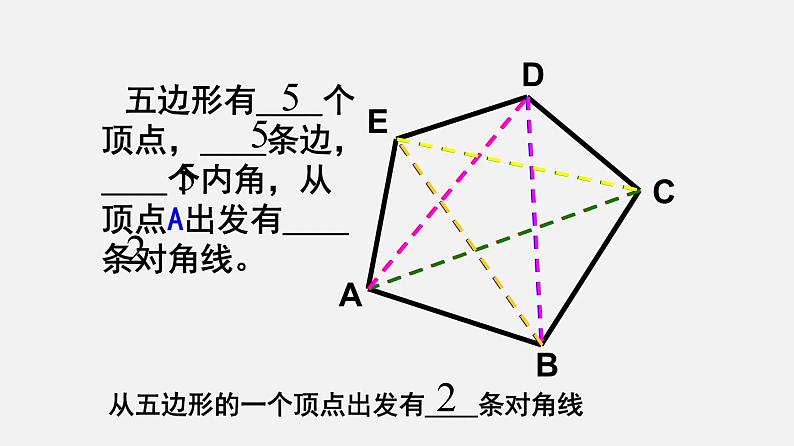
五边形有____个顶点，____条边，____个内角，从顶点A出发有____条对角线。
从五边形的一个顶点出发有____条对角线
n边形有____个顶点，____条边，____个内角，从顶点A出发有____条对角线。
从n边形的一个顶点出发有 条对角线
十二边形的内角和为 度．
从多边形的一个顶点出发画出相应的各条对角线,把求多边形的内角和转化为求几个三角形的内角和.
你还有其它求五边形内角和的方法吗?
例题1 求十边形的内角和.
答：这个多边形的边数为24.
3、一个多边形的内角和公式是什么？
由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形．
多边形内角和=（n-2）×180º
2、多边形的相关元素：
多边形的边、顶点、对角线、内角
清晨，小杰沿一个五边形广场周围的小路，他从AB段的M处出发，按逆时针方向奔跑一周。
请你观察并思考如下几个问题:
(1)小杰每从一条小路转到下一条小路时，身体转过的角是哪个角？
定义 多边形的一个内角的邻补角，叫做多边形的外角
多边形的外角中，与同一个内角相邻的外角有两个，它们互为对顶角
(2)他跑完一圈，回到起点，他转弯的角度和是多少度呢？
对多边形的每一个内角，从与它相邻的两个外角中取一个，这样所得的所有外角的和，叫做这个多边形的外角和
　　问题1：三角形外角和是多少？
　由 ∠1 +∠BAE =180°，∠2 +∠CBF =180°， ∠3 +∠ACD =180°， 得 ∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD =540°． 由 ∠1 + ∠2 + ∠3 = 180°，得 ∠BAE +∠CBF +∠ACD 　 = 540° - 180° = 360°．
3×180-(3-2)×180=360
　　问题2　如图，怎么求四边形的外角和呢？
由 ∠BAD +∠1 =180°， ∠ABC +∠2 =180°， ∠BCD +∠3 =180°， ∠ADC +∠4 =180°，得∠BAD + ∠1 + ∠ABC +∠2 +∠BCD +∠3 +∠ADC +∠4 =180°×4．由∠BAD +∠ABC +∠BCD +∠ADC =180°×2，得∠1 +∠2 +∠3 +∠4 =180°×4 - 180°×2 =360°．
4×180-(4-2)×180=360
3×180-(3-2)×180=360
5×180-(5-2)×180=360
6×180-(6-2)×180=360
　那怎么求n 边形（n 是不小于3 的任意整数）的外角和呢？
因为n边形的每个内角与它相邻的外角是邻补角（n 是不小于3的任意整数），它们的和是180°，所以n边形内角和加外角和等于n · 180°，所以n边形的外角和为：n · 180°-(n -2）· 180°= 360°
多边形的外角和等于360°
例1：一个多边形的每一个外角都是72°，那么这个多边形的内角和几度？
例2：一个多边形的内角和等于它的外角和的3倍，它是几边形？
例3：如图∠BCE是四边形ABCD的一个外角。如果∠BCE=∠A， 求：∠B+∠D的度数。想一想：如果∠B与∠D互为补角，那么∠BCE与∠A的大小相等吗？
1.若一个多边形的每一个外角都等于15°,则这个多边形的边数是________
2.若一个十边形的每个外角都相等，则它的每个外角的度数为________度，每个内角的度数为________度.
5.若一个多边形每一个内角都为162度，则它的边数是_______．
3.多边形的边数增加1，则内角和增加 _____度．外角和增加_____度
4.若一个八边形的每一个内角都相等,则它的一个内角的度数是______．
6. 若多边形的每个内角与相邻外角的比都是3∶2，求这个多边形的每个外角为多少度？它是几边形？
解:设这个多边形的每个内角与相邻外角的度数分别为 3x˚、2x˚. 则 3x+2x= 180. x=36 ∴ 2x=72. 360˚÷72˚ = 5答 : 这个多边形的每个外角为72˚，它是五边形。
思考：在一个多边形中,它的内角中最多有几个锐角?
因为一个多边形的外角和为360度，所以，外角最多可以有3个钝角；又因为多边形的内角与它的外角互为邻补角，所以，一个多边形中最多可以有3个锐角。
　　解：不存在．　　理由：如果存在这样的多边形，设它的一个外角 为x ，则对应的内角为180°- x ，
　　这个多边形的边数为：360°÷150°=2.4，而边数 应是整数，因此不存在这样的多边形．
解：设它的外角为X度.则它的内角为5X度依题意得： X+5X=180 6X=180.. X=30 因为任何一个多边形它的外角和为360°. 所以有360÷30=12边 这是一个每内角相等的12边形.