


所属成套资源:沪教版(五四制)数学八下课件PPT整套
沪教版 (五四制)八年级下册22.2 平行四边形备课课件ppt
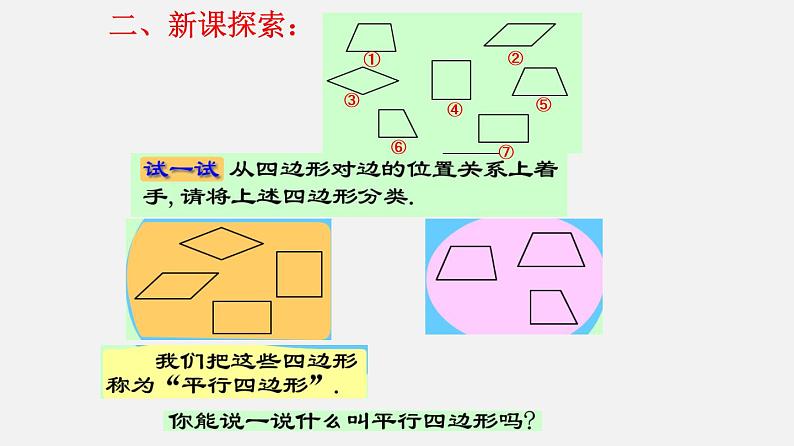
展开
这是一份沪教版 (五四制)八年级下册22.2 平行四边形备课课件ppt,共25页。PPT课件主要包含了课前复习,新课探索,平行四边形的性质,边推论角,对边相等,例题讲解等内容,欢迎下载使用。
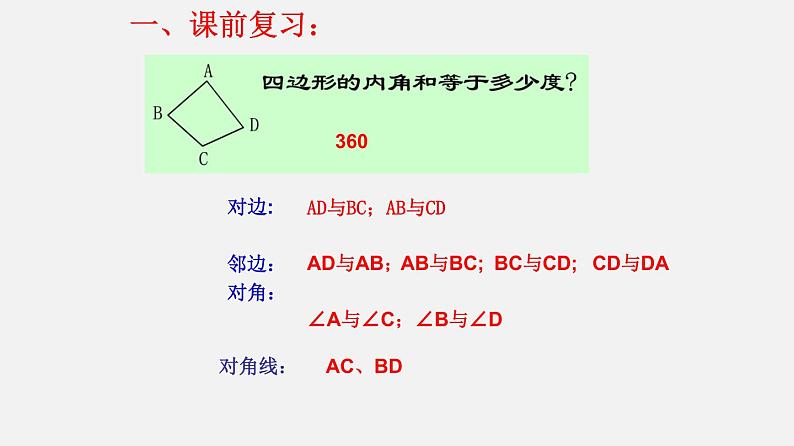
AD与BC;AB与CD
∠A与∠C;∠B与∠D
3.平行四边形的对角相等
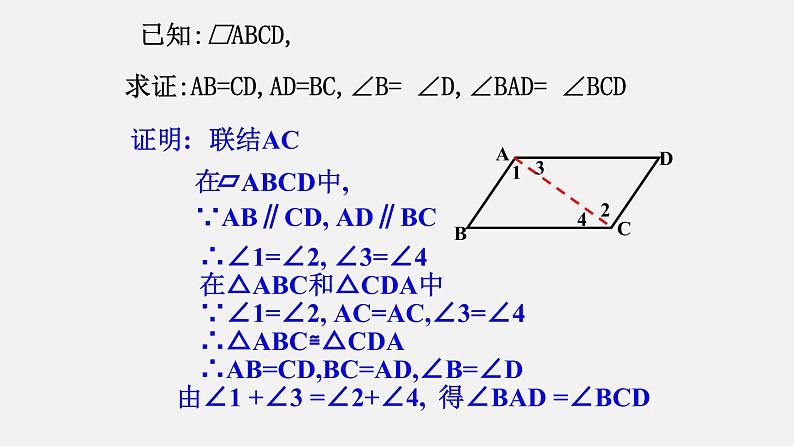
∵AB∥CD, AD∥BC
∴∠1=∠2, ∠3=∠4
在△ABC和△CDA中
∵∠1=∠2, AC=AC,∠3=∠4
∴AB=CD,BC=AD,∠B=∠D
由∠1 +∠3 =∠2+∠4,
得∠BAD =∠BCD
已知:□ABCD,求证:AB=CD,AD=BC,∠B= ∠D,∠BAD= ∠BCD
答:1、平行四边形的两组对边分别相等. 2、平行四边形的两组对角分别相等.
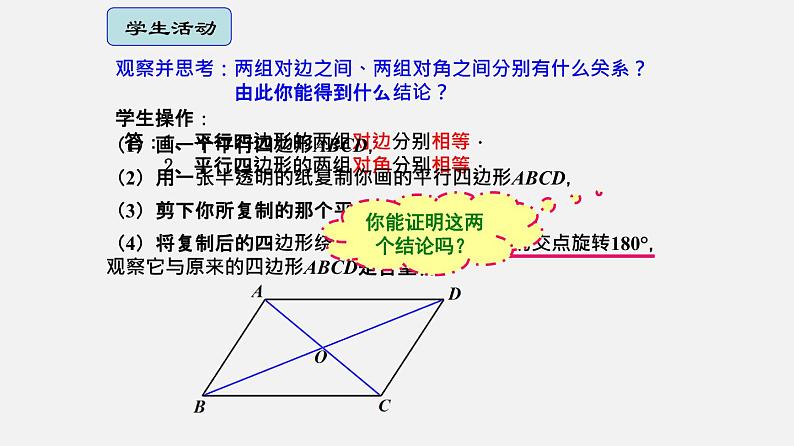
观察并思考:两组对边之间、两组对角之间分别有什么关系? 由此你能得到什么结论?
(1)画一个平行四边形ABCD,
(2)用一张半透明的纸复制你画的平行四边形ABCD,
(3)剪下你所复制的那个平行四边形,
(4)将复制后的四边形绕平行四边形的对角线的交点旋转180°,观察它与原来的四边形ABCD是否重合.
你能证明这两个结论吗?
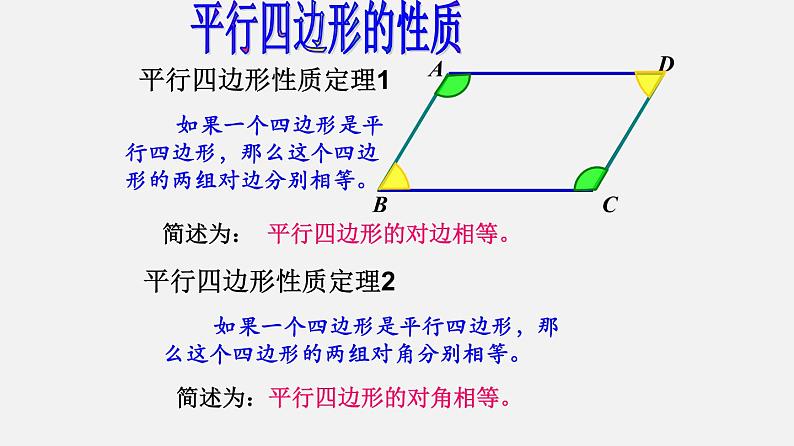
如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
简述为: 平行四边形的对边相等。
如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
简述为:平行四边形的对角相等。
如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
我们从另外一个角度来看,当平行线段转到一个特殊的位置(垂直).
平行线间的距离处处相等.
∵AB∥CD, AD∥BC,∴四边形ABCD是平行四边形(平行四边形的定义) ,∴ AB=CD(平行四边形的对边相等).
夹在两条平行线间的平行线段相等.
练一练:如图,四边形ABCD是平行四边形,点P是AD延长线上的一点,联结PB、PC,那么△ABC的面积和△PBC的面积是相等的.你能说出理由吗?
解:作 AE⊥BC, PF⊥BC,垂足为E、F, ∵四边形ABCD是平行四边形, ∴AD∥BC(平行四边形的定义), ∴AE= PF, ∴△ABC和△PBC是同底等高的三角形, ∴S△ABC= S△PBC .
表示平行四边形的周长.
例题1 小强用一根长度为36cm的铁丝围成了一个平行四边形的模型,其中一边是8cm,其它三边的长分别是多少?
平行四边形的周长公式是什么?
平行四边形的周长=2(AB+BC).
例题1 小强用一根长度为36cm的铁丝围成了一个平行四边形的模型,其中一边是8cm,其它三边的长分别是多少?
解:如图,把这个平行四边形模型表示为□ABCD,
由题意得AB的长是8cm.
答:其他三边的长分别是8cm、10cm、10cm.
∴AB=DC=8 cm,AD=BC(平行四边形的对边相等).
∵2(AB +BC)=36 cm,
∴BC=AD= 10 cm.
∵ 四边形ABCD是平行四边形,
例题2:如图,在□ABCD中,∠A比∠B大60°,求这个平行四边形各个内角度数.
运用所学的哪个性质求解?
运用平行四边形两组对角分别相等的性质来解.
∴∠A=∠C,∠B=∠D,(平行四边形对角相等),
AD∥BC(平行四边形定义),∴∠A+∠B=180°.
设∠A=x°,∠B=y°,又∠A比∠B大60°,则
∴∠A=∠C=120°,∠B=∠D=60°.
答:这个平行四边形各个内角度数分别为120°、120°、60°、60°.
解: ∵ 四边形ABCD是平行四边形,
1、(1)已知□ ABCD中,∠A=60°,求其他各内角的度数.
解:∵ 四边形ABCD是平行四边形,∴∠A=∠C,∠B=∠D (平行四边形的对角相等), AD∥BC(平行四边形的定义),∴∠A+∠B=180°.又∵∠A=60°,∴∠C=60°,∠B=∠D=120°,答:其他各内角的度数分别是60°、120°、120°.
(2)已知□ABCD的周长等于48,AB = 2BC,求各边的长.
解:∵ 四边形ABCD是平行四边形,∴AB=DC,AD=BC(平行四边形的对边相等).又∵2(AB +BC)=48,AB = 2BC,∴2(2BC +BC)=48,∴6BC=48,∴BC=8=AD,∴AB=DC=16.答:□ABCD各边的长分别是8、8、16、16.
2、如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB.(1) 指出图中所有的平行四边形;
(2) 求证:点A、B、C分别是线段EF、ED、DF的中点.
答:图中所有的平行四边形有:□EBCA,
证明:∵ ED∥AC,FD∥AB ,∴四边形ABDC是平行四边形(平行四边形的定义),∴BD=AC(平行四边形对边相等),
∴BD=EB,即点B是线段ED的中点.
同理 点A是线段EF的中点;点C是线段DF的中点.
一般按照逆时针的顺序写字母.
∠1=∠2, ∠3=∠4, AD=BC,∴ △AED≌△CFB(A.A .S).∴AE=CF.
3、已知:如图,□ ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E、F.求证:AE=CF.
证明: ∵ 四边形ABCD是平行四边形,∴AD=BC(平行四边形对边相等) , AD∥BC,∴∠1=∠2,又∵AE⊥BD,CF⊥BD,∴∠3=∠4=90°,在△AED和△CFB中,
对角相等、邻角互补、内角和360°
夹在两条平行线间的平行线段相等
例题1 小强用一根长度为36厘米的铁丝围成了一个平行四边形的模型,其中一边长是8厘米,其他三边的长分别是多少?
解:把这个平行四边形模型表示为 ABCD, 设AB的长是8厘米。
在 ABCD中,AB=CD,AD=BC
(平行四边形的对边相等)
∵AB=8(厘米),AB+DC+AD+BC=36(厘米)得DC=8(厘米),8+8+2AD=36(厘米),2AD=20(厘米)∴AD=10(厘米),BC=10(厘米)。
答:其他三边的长分别是8厘米、10厘米、10厘米。
例题2 在 ABCD中,∠A比∠B大60°,求这个平行四边形各个内角的度数?
解:在 ABCD中, ∠A= ∠C, ∠B= ∠D
(平行四边形的对角相等)
∵ AD∥BC (平行四边形的定义)∴ ∠A+ ∠B=180°
设∠A=X°, ∠B=Y°,又∠A比∠B大60°,
答: ∠A= ∠C=120°, ∠B= ∠D=60°。
1、如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED ∥AC,FD ∥AB。
(1) 图中的平行四边形有哪些?
(2)有哪些相等的线段?
(3)点A、B、C分别是线段EF、 ED、DF的什么点?为什么?
(4)已知∠E+∠ACB=116°,则∠E= ; 若∠F=27°,则∠ACF= 。
2、如图, 平行四边形 ABCD中,以BC、CD为边分别向外作正三角形BCE和CDF。求证:(1)AE=AF
(2)连接EF,则三角形AEF是等边三角形。
相关课件
这是一份沪教版 (五四制)八年级下册23.3 事件的概率备课课件ppt,共34页。PPT课件主要包含了事件的频率与概率,试一试,一起做一做,分析下面两个试验,概念辨析,归纳总结,第一次,第二次等内容,欢迎下载使用。
这是一份初中数学22.4 梯形备课ppt课件,共25页。PPT课件主要包含了等腰梯形,两腰相等,梯形有关定义,梯形可由三角形截得,课堂小结,各类四边形之间的关系等内容,欢迎下载使用。
这是一份初中数学沪教版 (五四制)八年级下册22.3 特殊的平行四边形备课ppt课件,共43页。PPT课件主要包含了复习备用,平行四边形的性质,对角线,对角相等邻角互补,对角线互相平分,知识点一矩形的定义,新知探究,平行四边形,有一个角是直角,新知归纳等内容,欢迎下载使用。









