数学8.4 三元一次方程组的解法教课课件ppt

这是一份数学8.4 三元一次方程组的解法教课课件ppt，共23页。PPT课件主要包含了化二元为一元，化归转化思想，消元法，流氓兔比加菲猫大1岁，求三个小动，物的年龄，流氓兔的年龄，加菲猫的年龄，米老鼠的年龄，x9y8z6等内容，欢迎下载使用。

1.理解三元一次方程组（simultaneus linear equatins with three unknwns）的概念．2.能解简单的三元一次方程组（simultaneus linear equatins with three unknwns）．
1.解二元一次方程组（simultaneus linear equatins with tw unknwns）有哪几种方法？
2.解二元一次方程组（simultaneus linear equatins with tw unknwns）的基本思路是什么？
二元一次方程组（simultaneus linear equatins with tw unknwns）
一元一次方程（linear equatins with ne unknwn）
代入消元法和加减消元法
思考：若含有3个未知数（unknwn）的方程组（simultaneus equatins）如何求解？
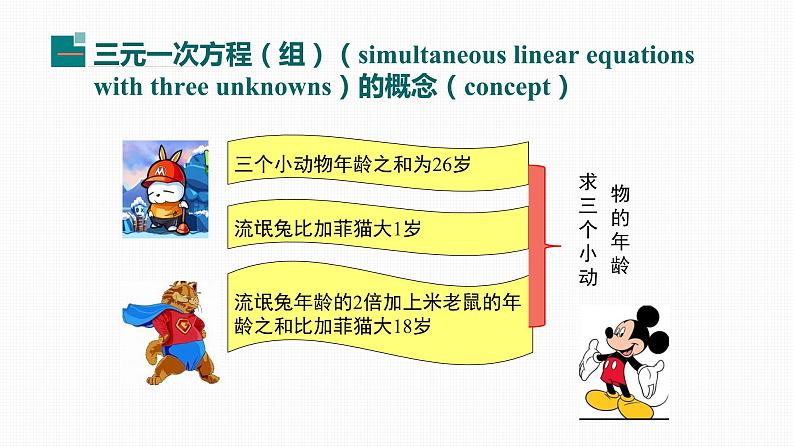
三个小动物年龄之和为26岁
流氓兔年龄的2倍加上米老鼠的年龄之和比加菲猫大18岁
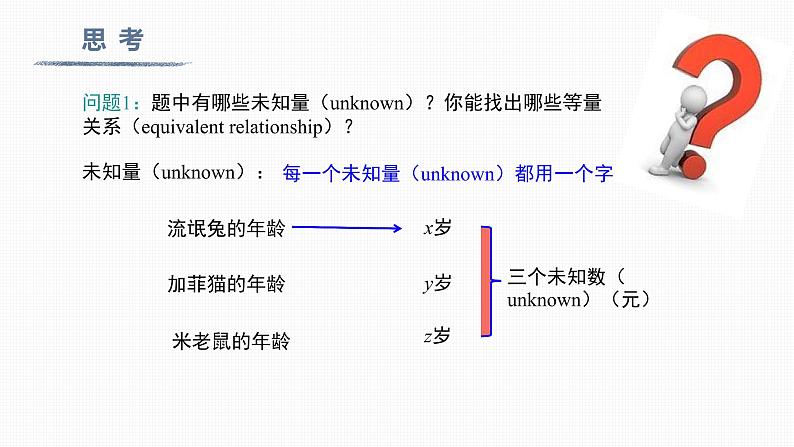
问题1：题中有哪些未知量（unknwn）？你能找出哪些等量关系（equivalent relatinship）？
未知量（unknwn）：
每一个未知量（unknwn）都用一个字母表示
三个未知数（unknwn）（元）
等量关系（equivalent relatinship）：
（1）流氓兔的年龄+加菲猫的年龄+米老鼠的年龄=26
（2）流氓兔的年龄-1=加菲猫的年龄
（3）2×流氓兔的年龄+米老鼠的年龄=加菲猫的年龄+18
用方程（equatin）表示等量关系（equivalent relatinship）.
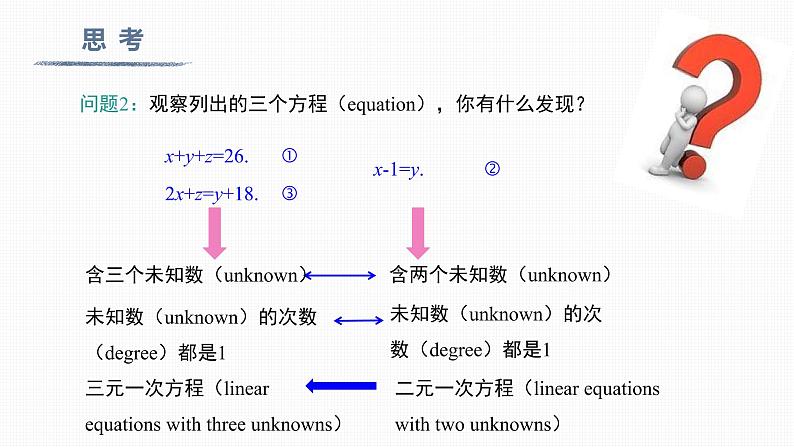
问题2：观察列出的三个方程（equatin），你有什么发现？
二元一次方程（linear equatins with tw unknwns）
三元一次方程（linear equatins with three unknwns）
含两个未知数（unknwn）
未知数（unknwn）的次数（degree）都是1
含三个未知数（unknwn）
因三个小动物的年龄必须同时满足上述三个方程（equatin），故将三个方程（equatin）联立在一起.
在这个方程组（simultaneus equatins）中，含有三个未知数（unknwn），每个方程（equatin）中所含未知数（unknwn）的项（term）的次数（degree）都是1，并且一共有三个方程（equatin），像这样的方程组（simultaneus equatins）叫做三元一次方程组（simultaneus linear equatins with three unknwns）.
下列方程组（simultaneus equatins）不是三元一次方程组（simultaneus linear equatins with three unknwns）的是 ( )
[注意] 组成三元一次方程组（simultaneus linear equatins with three unknwns）的三个一次方程（equatin）中，不一定要求每一个一次方程（equatin）都含有三个未知数（unknwn）．
类似二元一次方程组（simultaneus linear equatins with three unknwns）的解，三元一次方程组（simultaneus linear equatins with three unknwns）中各个方程（equatin）的公共解（cmmn slutin），叫做这个三元一次方程组（simultaneus linear equatins with three unknwns）的解（slutin）.
怎样解三元一次方程组（simultaneus linear equatins with three unknwns）呢？
能不能像以前一样“消元”，把“三元”化成“二元”呢？
例1：解方程组（simultaneus equatins）
解：由方程②得 x=y+1 ④ 把④分别代入（substitute）①③得 2y+z=22 ⑤ 3y-z=18 ⑥解由⑤⑥组成的二元一次方程组（simultaneus linear equatins with tw unknwns），得 y=8,z=6 把y=8代入（substitute）④，得x=9 所以原方程（equatin）的解（slutin）是
类似二元一次方程组的“消元”,把“三元”化成“二元”.
解三元一次方程组（simultaneus linear equatins with three unknwns）的基本思路是：通过“代入（substitute）”或“加减（additin r subtractin）”进行 ，把 转化为 ，使解三元一次方程组（simultaneus linear equatins with three unknwns）转化为解 ，进而再转化为解 .
例2：在等式 （equatin）y=ax2＋bx＋c中,当x=－1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值（value）.
解:根据题意，得三元一次方程组（simultaneus linear equatins with three unknwns）
a－b＋c= 0， ①4a＋2b＋c=3， ②25a＋5b＋c=60. ③
②－①， 得 a＋b=1 ④
③－①，得 4a＋b=10 ⑤
④与⑤组成二元一次方程组（simultaneus linear equatins with tw unknwns）
a＋b=1，4a＋b=10.
解这个方程组（simultaneus equatins），得
把 代入①，得
a=3，b=-2，c=-5.
例3 幼儿营养标准中要求每一个幼儿每天所需的营养量中应包含35单位的铁、70单位的钙和35单位的维生素.现有一批营养师根据上面的标准给幼儿园小朋友们配餐，其中包含A、B、C三种食物，下表给出的是每份（50g)食物A、B、C分别所含的铁、钙和维生素的量（单位）
（1）如果设食谱中A、B、C三种食物各为x、y、z份，请列出方程组（simultaneus equatins），使得A、B、C三种食物中所含的营养量刚好满足幼儿营养标准中的要求. （2）解该三元一次方程组（simultaneus linear equatins with three unknwns），求出满足要求的A、B、C的份数.
解：(1)由该食谱中包含35单位的铁、70单位的钙和35单位的维生素，得方程组（simultaneus equatins）
（2）-×4,-,得
通过回代，得 z=2,y=1,x=2.
答：该食谱中包含A种食物2份，B种食物1份，C种食物2份.
1.解方程组（simultaneus equatins） ,则x＝_____，y＝______，z＝_______.
【解析】通过观察未知数（unknwn）的系数（cefficient），可采取① +②求出y， ②+ ③求出z，最后再将y与z的值（value）代入（substitute）任何一个方程（equatin）求出x即可.
2.若x＋2y＋3z＝10，4x＋3y＋2z＝15，则x＋y＋z的值（value）为（ ）A.2 B.3 C.4 D.5
解析: 通过观察未知数（unknwn）的系数（cefficient），可采取两个方程（equatin）相加得，5x+5y+5z=25，所以x+y+z=5.
3.若|a－b－1|＋(b－2a＋c)2＋|2c－b|＝0，求a，b，c的值（value）．
解：因为三个非负数（nnnegative number）的和等于0，所以每个非负数（nnnegative number）都为0.可得方程组（simultaneus equatins） 解得
4.一个三位数（three-digit number），十位上的数字是个位上的数字的 ，百位上的数字与十位上的数字之和比个位上的数字大1.将百位与个位上的数字对调后得到的新三位数（three-digit number）比原三位数（three-digit number）大495，求原三位数（three-digit number）．
解：设原三位数（three-digit number）百位、十位、个位上的数字分别为x、y、z.由题意，得解得答：原三位数（three-digit number）是368.