




高考数学一轮复习配套课件 第九章 第七节 抛物线
展开·最新考纲·1.掌握抛物线的定义、几何图形和标准方程.2.掌握抛物线的简单几何性质.(范围、对称性、顶点、离心率)3.理解数形结合的思想.4.了解抛物线的简单应用.
·考向预测·考情分析:抛物线的定义、标准方程,抛物线的几何性质,直线与抛物线的位置关系,仍是高考的热点,题型仍将是选择题,填空题,有时出现解答题.学科素养:通过抛物线的标准方程与几何性质考查数学运算的核心素养;通过抛物线的定义、直线与抛物线的位置关系考查数学抽象、直观想象的核心素养.
一、必记2个知识点1.抛物线的定义平面内与一个定点F和一条定直线l(F∉l)的距离________的点的轨迹叫做抛物线,点F叫做抛物线的________,直线l叫做抛物线的________.[注意] 当定点在定直线上时,轨迹为过定点F与定直线l垂直的一条直线.
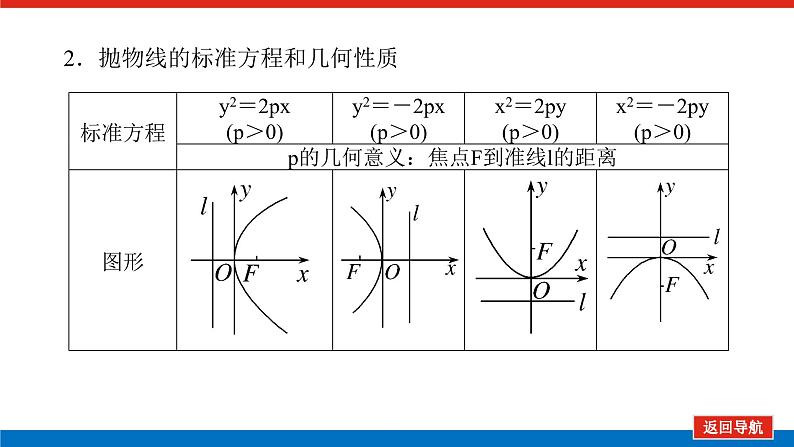
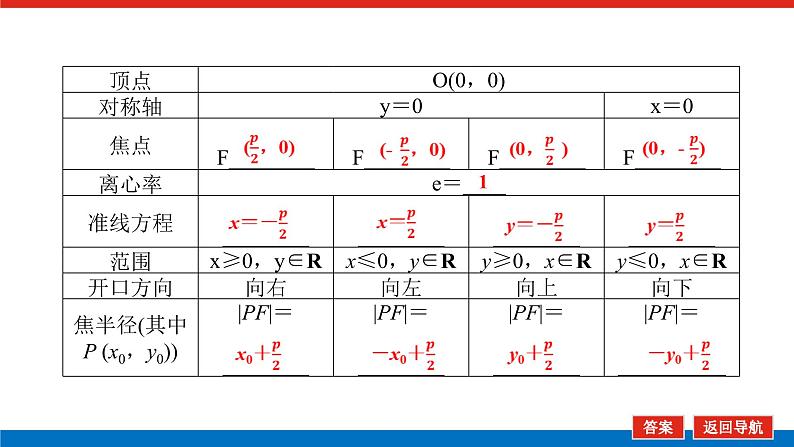
2.抛物线的标准方程和几何性质
(二)教材改编2.[选修2-1·P69例4改编]过抛物线y2=4x的焦点的直线l交抛物线于P(x1,y1),Q(x2,y2)两点,如果x1+x2=6,则|PQ|等于( )A.9 B.8 C.7 D.6
解析:抛物线y2=4x的焦点为F(1,0),准线方程为x=-1,根据题意可得|PQ|=|PF|+|QF|=x1+1+x2+1=x1+x2+2=8.
3.[选修1-1·P64A组T4(2)题改编]顶点在原点,且过点P(-2,3)的抛物线的标准方程是__________________.
5.(忽视焦点的位置致误)若抛物线的焦点在直线x-2y-4=0上,则此抛物的标准方程为__________________.
y2=16x或x2=-8y
解析:当焦点在x轴上时,根据y=0,x-2y-4=0可得焦点坐标为(4,0),所以抛物线的标准方程为y2=16x;当焦点在y轴上时,根据x=0,x-2y-4=0可得焦点坐标为(0,-2),所以抛物线的标准方程为x2=-8y.
(四)走进高考6.[2021·北京卷]已知抛物线C:y2=4x,C的焦点为F,点M在C上,若|FM|=6,则M的横坐标是_____.
解析:设点M的坐标为(x0,y0),则有|FM|=x0+1=6,解得x0=5.
(2)设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,若B(3,2),则|PB|+|PF|的最小值为________.
解析:(2)如图,过点B作BQ垂直准线于点Q,交抛物线于点P1,则|P1Q|=|P1F|. 则有|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=4.即|PB|+|PF|的最小值为4.
一题多变 1.(变条件)将例1(2)中的B点坐标改为(3,4),试求|PB|+|PF|的最小值为________.
2.(变问题)若本例1(2)条件不变,求P到准线l的距离与P到直线3x+4y+7=0的距离之和的最小值是_____.
【对点训练】1.[2022·湖北武汉高三月考]已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|=( )A.4 B.6C.8 D.10
反思感悟 1.求抛物线的标准方程的方法(1)先定位:根据焦点或准线的位置.(2)再定形:即根据条件求p.2.抛物线性质的应用技巧(1)利用抛物线方程确定及应用其焦点、准线时,关键是将抛物线方程化成标准方程.(2)要结合图形分析,灵活运用平面图形的性质简化运算.
反思感悟 解决直线与抛物线位置关系问题的方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB|=x1+x2+p,若不过焦点,则必须用一般弦长公式.(2)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.[提醒] 涉及弦的中点、斜率时一般用“点差法”求解.
微专题35 活用抛物线焦点弦的几个结论
数学抽象素养水平表现为能够在得到的数学结论的基础上形成新命题,能够针对具体的问题运用数学方法解决问题,而新命题、新结论有助于数学运算,两者相辅相成,本课时抛物线的焦点弦问题的四个常用结论即为具体表现之一.
[方法总结]该种类型题目通过抛物线的特殊性质,脱离于传统的联立方程组求解,较为迅速的得到结果,体现了模式化的认识特征,将特殊的概念结论广泛地、抽象地应用于数学题目,体现了数学抽象的素养;代入数值进行计算,体现数学运算的素养.
[变式训练1] 已知抛物线C:y2=2px(p>0)的焦点F到其准线的距离为4,圆M:(x-2)2+y2=1,过F的直线l与抛物线C和圆M从上到下依次交于A,P,Q,B四点,则|AP|+4|BQ|的最小值为________.
[变式训练2] 经过抛物线C:y2=2px(p>0)的焦点F,倾斜角为30°的直线l与C交于A,B两点,若线段AB的中点M的横坐标为7,那么p=_____.
[方法总结]该题将求弦长问题,通过焦半径与p之间的关系,转化为焦半径问题,体现了数学抽象的素养;通过焦半径结论代入计算,体现了数学运算的素养.
适用于新教材2024版高考数学一轮总复习第九章平面解析几何第七节抛物线课件北师大版: 这是一份适用于新教材2024版高考数学一轮总复习第九章平面解析几何第七节抛物线课件北师大版,共29页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,常用结论,答案C等内容,欢迎下载使用。
备战2024高考一轮复习数学(理) 第九章 解析几何 第七节 抛物线课件PPT: 这是一份备战2024高考一轮复习数学(理) 第九章 解析几何 第七节 抛物线课件PPT,共32页。PPT课件主要包含了距离相等,答案A,答案B,答案D,答案x2=4y,答案C,答案22等内容,欢迎下载使用。
高中数学高考2018高考数学(文)大一轮复习课件 第八章 解析几何 第七节 抛物线: 这是一份高中数学高考2018高考数学(文)大一轮复习课件 第八章 解析几何 第七节 抛物线,共27页。












