高考数学一轮复习配套课件 第十二章 第三节 直接证明和间接证明

这是一份高考数学一轮复习配套课件 第十二章 第三节 直接证明和间接证明，共36页。PPT课件主要包含了必备知识基础落实，关键能力考点突破，假设Q不成立，第一个值n0，n＝k＋1，答案A等内容，欢迎下载使用。
·最新考纲·1．了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程、特点．2．了解间接证明的一种基本方法——反证法；了解反证法的思考过程、特点．
·考向预测·考情分析：直接证明与间接证明是高中数学的重要推理方法，它们仍是高考的考点，题型将是选择或填空题．学科素养：通过直接证明和间接证明的应用考查逻辑推理的核心素养．
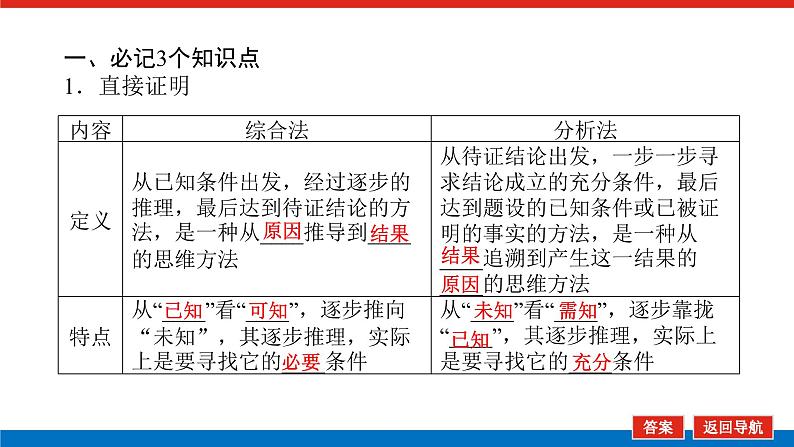
一、必记3个知识点1．直接证明
2.间接证明——反证法要证明某一结论Q是正确的，但不直接证明，而是先去____________(即Q的反面非Q是正确的)，经过正确的推理，最后得出________，因此说明非Q是______的，从而断定结论Q是________的，这种证明方法叫做反证法．3．数学归纳法一般地，证明一个与正整数n有关的命题，可按下列步骤进行：(1)(归纳奠基)证明当n取___________ (n0∈N*)时命题成立．(2)(归纳递推)假设n＝k(k≥n0，k∈N*)时命题成立，证明当________时命题也成立．只要完成这两个步骤，就可以断定命题对____________________都成立，上述证明方法叫做数学归纳法．
从n0开始的所有正整数n
二、必明2个常用结论1．分析法与综合法的应用特点：对较复杂的问题，常常先从结论进行分析，寻求结论与条件的关系，找到解题思路，再运用综合法证明；或两种方法交叉使用．2．利用反证法证明的特点：要假设结论错误，并用假设的命题进行推理，如果没有用假设命题推理而推出矛盾结果，其推理过程是错误的．
三、必练2类基础题(一)判断正误1．判断下列说法是否正确(请在括号中打“√”或“×”)．(1)综合法是直接证明，分析法是间接证明．(　　)(2)分析法是从要证明的结论出发，逐步寻找使结论成立的充要条件．(　　)(3)反证法是指将结论和条件同时否定，推出矛盾．(　　)
反思感悟　综合法证题的思路与方法
反思感悟　分析法的证题思路分析法的证题思路是“执果索因”，即从“未知”看“需知”，逐步靠拢“已知”或本身已经成立的定理、性质或已经证明成立的结论等．通常采用“欲证—只需证—已知”的格式，在表达中要注意叙述形式的规范．
反思感悟　反证法证明问题的一般步骤(1)反设——假设命题的结论不成立，即假设原结论的反面为真；(2)归谬——把“反设”作为条件，经过一系列正确的推理，得出矛盾；(3)存真——由矛盾结果断定反设错误，从而肯定原结论成立．应用反证法时，当原命题的结论的反面有多种情况时，要对结论的反面的每一种情况都进行讨论，从而达到否定结论的目的．
反思感悟　数学归纳法证明不等式的适用范围及关键(1)适用范围：当遇到与正整数n有关的不等式证明时，若用其他方法不易证，则可考虑应用数学归纳法．(2)关键：由n＝k时命题成立证n＝k＋1时命题也成立，在归纳假设使用后可运用比较法、综合法、分析法、放缩法等来加以证明，充分应用基本不等式、不等式的性质等放缩技巧，使问题得以简化.
角度2　归纳——猜想——证明[例5]　设函数f(x)＝ln (1＋x)，g(x)＝xf′(x)，x≥0，其中f′(x)是f(x)的导函数．(1)令g1(x)＝g(x)，gn＋1(x)＝g(gn(x))，n∈N*，求gn(x)的表达式；
(2)若f(x)≥ag(x)恒成立，求实数a的取值范围．
反思感悟　归纳—猜想—证明问题的一般步骤第一步：计算数列前几项或特殊情况，观察规律猜测数列的通项或一般结论；第二步：验证一般结论对第一个值n0(n0∈N*)成立；第三步：假设当n＝k(k≥n0，k∈N*)时结论成立，证明当n＝k＋1时结论也成立；第四步：下结论，由上可知结论对任意n≥n0，n∈N*成立．