天津市南开区美达菲学校2022-2023学年九年级上学期9月线上教学阶段性验收数学试题(解析版)

这是一份天津市南开区美达菲学校2022-2023学年九年级上学期9月线上教学阶段性验收数学试题(解析版)，共21页。试卷主要包含了2+3，下列结论等内容，欢迎下载使用。
天津市南开区美达菲学校2022-2023学年九年级上学期9月线上教学阶段性验收数学试题（附答案与解析）
一.选择题（共10小题，每道题4分，共40分。）
1．（4分）下列事件不属于随机事件的是（　　）
A．打开电视正在播放新闻联播
B．某人骑车经过十字路口时遇到红灯
C．抛掷一枚硬币，出现正面朝上
D．若今天星期一，则明天是星期二
2．（4分）不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别．从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是（　　）
A． B． C． D．
3．（4分）用配方法解一元二次方程2x2﹣4x﹣1＝0，配方正确的是（　　）
A．（x﹣1）2＝ B．（x﹣1）2＝2 C．（x﹣2）2＝ D．（x﹣2）2＝2
4．（4分）有一个人患流感，经过两轮传染后共有81个人患流感，每轮传染中平均一个人传染几个人？设每轮传染中平均一个人传染x个人，可列方程为（　　）
A．1+2x＝81 B．1+x2＝81
C．1+x+x2＝81 D．1+x+x（1+x）＝81
5．（4分）若二次函数y＝﹣x2+6x+c的图象经过点A（﹣1，y1），B（2，y2），C（5，y3），则y1，y2，y3的大小关系正确的为（　　）
A．y1＞y3＞y2 B．y2＞y3＞y1 C．y1＞y2＞y3 D．y3＞y1＞y2
6．（4分）对于抛物线y＝﹣（x+1）2+3，下列结论：
①抛物线的开口向下；
②对称轴为直线x＝1；
③顶点坐标为（﹣1，3）；
④x＞1时，y随x的增大而减小；
⑤抛物线与y轴的交点坐标为（0，3）．
其中正确的有（　　）个．
A．1 B．2 C．3 D．4
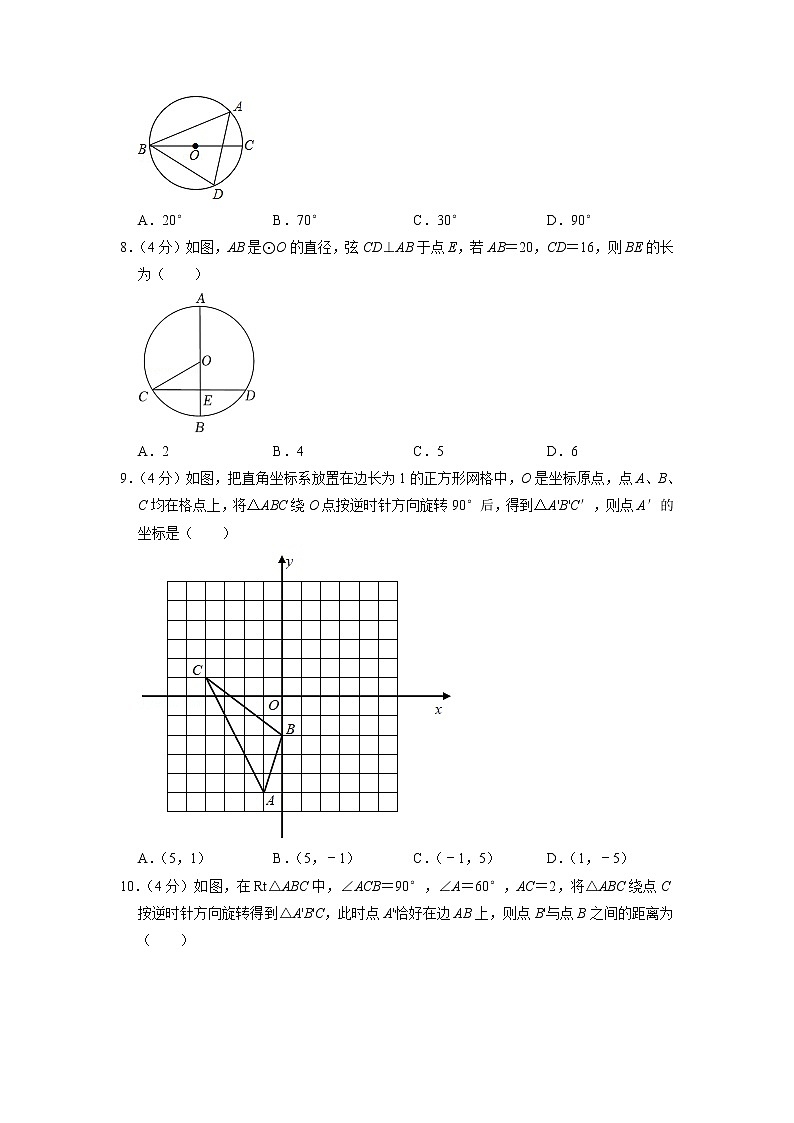
7．（4分）如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（　　）

A．20° B．70° C．30° D．90°
8．（4分）如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝20，CD＝16，则BE的长为（　　）

A．2 B．4 C．5 D．6
9．（4分）如图，把直角坐标系放置在边长为1的正方形网格中，O是坐标原点，点A、B、C均在格点上，将△ABC绕O点按逆时针方向旋转90°后，得到△A'B'C′，则点A′的坐标是（　　）

A．（5，1） B．（5，﹣1） C．（﹣1，5） D．（1，﹣5）
10．（4分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝2，将△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在边AB上，则点B'与点B之间的距离为（　　）

A．4 B．2 C．3 D．
二.填空题（共5小题，每道题4分，共20分）
11．（4分）关于x的一元二次方程ax2﹣2x+2＝0有两个不相等实数根，则a的取值范围为 　 　．
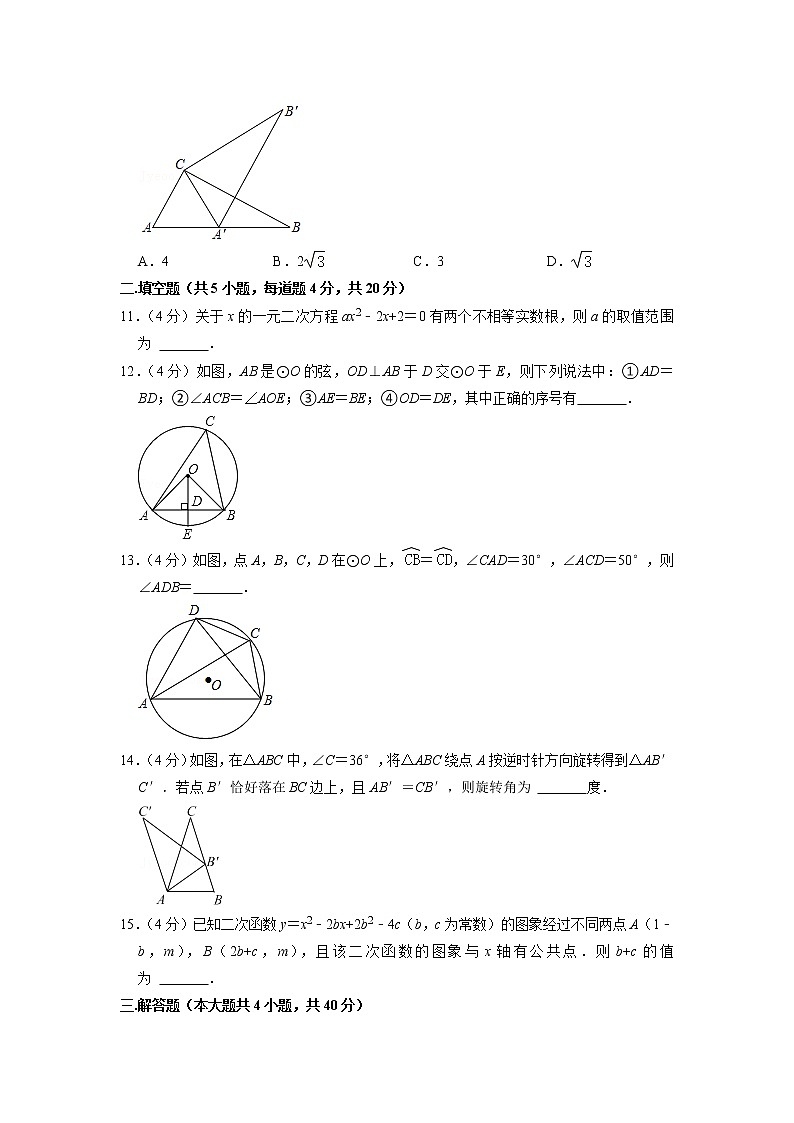
12．（4分）如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法中：①AD＝BD；②∠ACB＝∠AOE；③AE＝BE；④OD＝DE，其中正确的序号有　 　．

13．（4分）如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝　 　．

14．（4分）如图，在△ABC中，∠C＝36°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB′＝CB′，则旋转角为 　 　度．

15．（4分）已知二次函数y＝x2﹣2bx+2b2﹣4c（b，c为常数）的图象经过不同两点A（1﹣b，m），B（2b+c，m），且该二次函数的图象与x轴有公共点．则b+c的值为 　 　．
三.解答题（本大题共4小题，共40分）
16．（10分）解方程：
（1）x2﹣2x﹣3＝0；
（2）x2﹣16＝2（x+4）．
17．（10分）已知二次函数y＝x2﹣4x+3．
（Ⅰ）将y＝x2﹣4x+3化成y＝a（x﹣h）2+k的形式：　 　；
（Ⅱ）抛物线与x轴交点坐标为 　 　；
（Ⅲ）在平面直角坐标系中，画出这个二次函数的图象；
（Ⅳ）当y＜0时，x的取值范围是 　 　；
（Ⅴ）当0＜x＜3时，y的取值范围是 　 　．

18．（10分）已知Rt△ABC中，∠ACB＝90°，AC＝4，∠B＝30°，把边AC绕点A逆时针旋转，点C的对应点D落在边AB上．
（Ⅰ）如图①，则线段AD的长为 　 　，旋转角的大小为 　 　，点D到直线BC的距离为 　 　；
（Ⅱ）点P是直线BC上的一个动点，连接AP，把△ACP绕点A逆时针旋转，使边AC与AD重合，得△ADQ，点Q与点P是对应点．如图②，当点P在边CB上，且CP＝3时，求PQ的长．

19．（10分）如图，抛物线y＝x2+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C．直线y＝x﹣2经过B、C两点，点P是抛物线上一动点．
（1）求抛物线的解析式；
（2）当点P在BC下方运动时，求△BCP面积的最大值．
（3）连接OP，把△OCP沿着y轴翻折，使点P落在P'的位置，四边形CPOP'能否构成菱形，若能，求出点P的坐标，如不能，请说明理由；
（4）把抛物线y＝x2+bx+c向上平移1.5个单位，再向左平移m个单位，使顶点落在△ABC内部，求直接写出点m的取值范围．


天津市南开区美达菲学校2022-2023学年九年级上学期9月线上教学阶段性验收数学试题参考答案与试题解析
一.选择题（共10小题，每道题4分，共40分。）
1．（4分）下列事件不属于随机事件的是（　　）
A．打开电视正在播放新闻联播
B．某人骑车经过十字路口时遇到红灯
C．抛掷一枚硬币，出现正面朝上
D．若今天星期一，则明天是星期二
【分析】根据事件发生的可能性大小判断即可．
【解答】解：A、打开电视正在播放新闻联播是随机事件；
B、某人骑车经过十字路口时遇到红灯是随机事件；
C、抛掷一枚硬币，出现正面朝上是随机事件；
D、若今天星期一，则明天是星期二是必然事件；
故选：D．
【点评】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
2．（4分）不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别．从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是（　　）
A． B． C． D．
【分析】列表得出所有等可能的情况数，找出第一次摸到红球、第二次摸到绿球的情况数，即可确定出所求的概率．
【解答】解：列表如下：

红
绿
红
（红，红）
（绿，红）
绿
（红，绿）
（绿，绿）
所有等可能的情况有4种，其中第一次摸到红球、第二次摸到绿球的有1种情况，
所以第一次摸到红球、第二次摸到绿球的概率为，
故选：A．
【点评】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率＝所求情况数与总情况数之比．
3．（4分）用配方法解一元二次方程2x2﹣4x﹣1＝0，配方正确的是（　　）
A．（x﹣1）2＝ B．（x﹣1）2＝2 C．（x﹣2）2＝ D．（x﹣2）2＝2
【分析】将常数项移到方程的右边，再将二次项系数化为1，继而两边都加上一次项系数一半的平方配成完全平方式后即可．
【解答】解：∵2x2﹣4x﹣1＝0，
∴2x2﹣4x＝1，
∴x2﹣2x＝，
则x2﹣2x+1＝+1，即（x﹣1）2＝，
故选：A．
【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
4．（4分）有一个人患流感，经过两轮传染后共有81个人患流感，每轮传染中平均一个人传染几个人？设每轮传染中平均一个人传染x个人，可列方程为（　　）
A．1+2x＝81 B．1+x2＝81
C．1+x+x2＝81 D．1+x+x（1+x）＝81
【分析】平均一人传染了x人，根据有一人患了流感，第一轮有（x+1）人患流感，第二轮共有x+1+（x+1）x人，即81人患了流感，由此列方程求解．
【解答】解：设平均一人传染了x人，第一轮有（x+1）人患流感，第二轮共有x+1+（x+1）x人，
根据题意得：x+1+（x+1）x＝81，
故选：D．
【点评】本题考查了一元二次方程的应用，关键是得到两轮传染数量关系，从而可列方程求解．
5．（4分）若二次函数y＝﹣x2+6x+c的图象经过点A（﹣1，y1），B（2，y2），C（5，y3），则y1，y2，y3的大小关系正确的为（　　）
A．y1＞y3＞y2 B．y2＞y3＞y1 C．y1＞y2＞y3 D．y3＞y1＞y2
【分析】先根据二次函数图象上点的坐标特征，分别计算出自变量为2、﹣2和﹣5所对应的函数值，然后比较函数的大小即可．
【解答】解：当x＝﹣1时，y1＝﹣x2+6x+c＝﹣1﹣6+c＝﹣7+c；
当x＝2时，y2＝﹣x2+6x+c＝﹣4+12+c＝8+c；
当x＝5时，y3＝﹣x2+6x+c＝﹣25+30+c＝5+c，
所以y2＞y3＞y1．
故选：B．
【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
6．（4分）对于抛物线y＝﹣（x+1）2+3，下列结论：
①抛物线的开口向下；
②对称轴为直线x＝1；
③顶点坐标为（﹣1，3）；
④x＞1时，y随x的增大而减小；
⑤抛物线与y轴的交点坐标为（0，3）．
其中正确的有（　　）个．
A．1 B．2 C．3 D．4
【分析】根据二次函数的性质对各小题分析判断即可得解．
【解答】解：①∵a＝﹣＜0，
∴抛物线的开口向下，正确；
②对称轴为直线x＝﹣1，故本小题错误；
③顶点坐标为（﹣1，3），正确；
④∵x＞﹣1时，y随x的增大而减小，
∴x＞1时，y随x的增大而减小一定正确；
⑤抛物线与y轴的交点坐标为（0，），故本小题错误；
综上所述，结论正确的个数是①③④共3个．
故选：C．
【点评】本题考查了二次函数的性质，主要利用了抛物线的开口方向、对称轴、顶点坐标，以及二次函数的增减性．
7．（4分）如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（　　）

A．20° B．70° C．30° D．90°
【分析】连接AC，如图，根据圆周角定理得到∠BAC＝90°，∠ACB＝∠ADB＝70°，然后利用互余计算∠ABC的度数．
【解答】解：连接AC，如图，
∵BC是⊙O的直径，
∴∠BAC＝90°，
∵∠ACB＝∠ADB＝70°，
∴∠ABC＝90°﹣70°＝20°．
故选：A．

【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
8．（4分）如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝20，CD＝16，则BE的长为（　　）

A．2 B．4 C．5 D．6
【分析】由垂径定理可求得AB⊥CD及CE的长，再利用勾股定理可求解OE的长，进而可求解．
【解答】解：∵AB是⊙O的直径，弦CD⊥AB于点E，AB＝20，
∴CO＝OB＝10，AB⊥CD，CE＝DE＝CD，
∵CD＝16，
∴CE＝8，
在Rt△COE中，OE＝，
∴BE＝OB﹣OE＝10﹣6＝4，
故选：B．
【点评】本题主要考查垂径定理，勾股定理，求解OE的长是解题的关键．
9．（4分）如图，把直角坐标系放置在边长为1的正方形网格中，O是坐标原点，点A、B、C均在格点上，将△ABC绕O点按逆时针方向旋转90°后，得到△A'B'C′，则点A′的坐标是（　　）

A．（5，1） B．（5，﹣1） C．（﹣1，5） D．（1，﹣5）
【分析】利用旋转变换的性质分别作出A，B，C的对应点A′，B′，C′即可．
【解答】解：观察图象可知，A′（5，﹣1）．

故选：B．
【点评】本题考查坐标与图形变化﹣旋转，解题的关键是正确作出图形，属于中考常考题型．
10．（4分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝2，将△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在边AB上，则点B'与点B之间的距离为（　　）

A．4 B．2 C．3 D．
【分析】由旋转的性质，可证△ACA'、△BCB'都是等边三角形，由勾股定理求出BC的长即可．
【解答】解：如图，连接BB'，

∵将△ABC绕点C按逆时针方向旋转得到△A'B'C，
∴∠BCB'＝∠ACA'，CB＝CB'，CA＝CA'，
∵∠A＝60°，
∴△ACA'是等边三角形，∠ABC＝30°，
∴∠ACA'＝60°，AB＝2AC，
∴∠BCB'＝60°，
∴△BCB'是等边三角形，
∴BB'＝BC，
在Rt△ABC中，AB＝2AC＝4，
∴BC＝＝＝2，
∴BB'＝2，
故选：B．
【点评】本题主要考查了旋转的性质，等边三角形的判定与性质，勾股定理等知识，熟练掌握旋转的性质是解题的关键．
二.填空题（共5小题，每道题4分，共20分）
11．（4分）关于x的一元二次方程ax2﹣2x+2＝0有两个不相等实数根，则a的取值范围为 　a＜且a≠0　．
【分析】根据一元二次方程的定义和判别式的意义得到a≠0且Δ＝（﹣2）2﹣4a×2＞0，然后求解不等式即可．
【解答】解：根据题意得a≠0且Δ＝（﹣2）2﹣4a×2＞0，
解得a＜且a≠0，
故答案为a＜且a≠0．
【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．
12．（4分）如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法中：①AD＝BD；②∠ACB＝∠AOE；③AE＝BE；④OD＝DE，其中正确的序号有　①②③　．

【分析】由AB为圆的直径，且与OD垂直，根据垂径定理得到D为AB中点，且E为弧AB的中点，即弧AE等于弧BE，由D为AB中点得到AD＝BD，故选项①正确；由等弧对等弦得到AE＝BE，故选项③正确；再由等弧对等角得到∠AOE＝∠BOE＝∠AOB，又根据同弧所对的圆周角等于它所对圆心角的一半，得到∠ACB＝∠AOB，等量代换即可得到∠ACB＝∠AOE，故选项②正确；若OD＝DE，即可得到OD等于半径OA的一半，根据直角三角形中一直角边等于斜边的一半，这条直角边所对的角为30°，而原题没有此条件，故选项④错误．
【解答】解：∵AB是⊙O的弦，OD⊥AB于D交⊙O于E，
∴D为AB的中点，且＝，
∴AD＝BD，选项①正确；
∴AE＝BE（等弧对等弦），选项③正确；
∵＝，
∴∠AOE＝∠BOE＝∠AOB，
又∵圆心角∠AOB和圆周角∠ACB都对，
∴∠ACB＝∠AOB，
∴∠AOE＝∠ACB，选项②正确；
若OD＝DE，得到OD＝OE＝OA，又△ADO为直角三角形，
∴∠OAD＝30°，题中没有此条件，选项④错误，
综上，正确的选项有①②③．
故答案为：①②③
【点评】此题考查了垂径定理，以及圆周角定理，垂径定理可理解为：如果一条直线满足：过圆心、平分弦、垂直弦、平分优弧、平分劣弧这五个结论中的任两个，其余三个结论一定成立，对圆周角和圆心角进行相互转换是处理圆周角、圆心角问题时常用的方法，同时注意同圆或等圆中，弧、弦及圆心角，若一组对应量相等，其余两对对应量也相等．
13．（4分）如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝　70°　．

【分析】直接利用圆周角定理以及结合三角形内角和定理得出∠ACB＝∠ADB＝180°﹣∠CAB﹣∠ABC，进而得出答案．
【解答】解：∵＝，∠CAD＝30°，
∴∠CAD＝∠CAB＝30°，
∴∠DBC＝∠DAC＝30°，
∵∠ACD＝50°，
∴∠ABD＝50°，
∴∠ADB＝∠ACB＝180°﹣∠CAB﹣∠ABC＝180°﹣50°﹣30°﹣30°＝70°．
故答案为：70°．
【点评】此题主要考查了圆周角定理以及三角形内角和定理，正确得出∠ABD度数是解题关键．
14．（4分）如图，在△ABC中，∠C＝36°，将△ABC绕点A按逆时针方向旋转得到△AB′C′．若点B′恰好落在BC边上，且AB′＝CB′，则旋转角为 　36　度．

【分析】由旋转的性质可得∠C＝∠C'，AB＝AB'，由等腰三角形的性质可得∠C＝∠CAB'，∠B＝∠AB'B，由三角形的外角性质和三角形内角和定理可求解．
【解答】解：∵AB'＝CB'，
∴∠C＝∠CAB'＝36°，
∴∠AB'B＝∠C+∠CAB'＝2∠C，
∵将△ABC绕点A按逆时针方向旋转得到△AB'C'，
∴∠C＝∠C'，AB＝AB'，
∴∠B＝∠AB'B＝2∠C，
∵∠B+∠C+∠CAB＝180°，
∴3∠C+∠CAB＝180°，
∵∠C＝36°，
∴∠CAB＝180°﹣3×36°＝72°，
∴旋转角的度数＝∠BAB'＝∠BAC﹣∠CAB'＝36°，
故答案为：36．
【点评】本题考查了旋转的性质，等腰三角形的性质，灵活运用这些的性质解决问题是本题的关键．
15．（4分）已知二次函数y＝x2﹣2bx+2b2﹣4c（b，c为常数）的图象经过不同两点A（1﹣b，m），B（2b+c，m），且该二次函数的图象与x轴有公共点．则b+c的值为 　3　．
【分析】根据抛物线对称性可得抛物线对称轴为直线x＝﹣＝，从而可得c＝b﹣1，由抛物线与x轴有交点可得Δ＝（﹣2b）2﹣4（2b2﹣4c）≥0，将c＝b﹣1代入可得b＝2，c＝1，进而求解．
【解答】解：∵抛物线经过不同两点A（1﹣b，m），B（2b+c，m），
∴抛物线对称轴为直线x＝﹣＝，
即b＝，整理得c＝b﹣1，
∵抛物线与x轴有交点，
Δ＝（﹣2b）2﹣4（2b2﹣4c）
＝4b2﹣8b2+16c
＝﹣4b2+16（b﹣1）
＝﹣4（b﹣2）2，
∴﹣4（b﹣2）2≥0，
∴b＝2，c＝b﹣1＝1，
∴b+c＝2+1＝3．
故答案为：3．
【点评】本题二次函数图象与系数的关系，解题关键是掌握二次函数的性质，掌握二次函数与x轴交点与判别式Δ的关系．
三.解答题（本大题共4小题，共40分）
16．（10分）解方程：
（1）x2﹣2x﹣3＝0；
（2）x2﹣16＝2（x+4）．
【分析】（1）先把方程的左边分解因式，再得到两个一次方程，再解一次方程即可；
（2）先把方程化为（x+4）（x﹣4）﹣2（x+4）＝0，再把左边分解因式，再解方程即可．
【解答】解：（1）解：x2﹣2x﹣3＝0，
∴（x﹣3）（x+1）＝0，
∴x﹣3＝0或x+1＝0，
解得：x1＝3，x2＝﹣1；
（2）x2﹣16＝2（x+4）
整理得：（x+4）（x﹣4）﹣2（x+4）＝0，
∴（x+4）（x﹣6）＝0，
∴x+4＝0或x﹣6＝0，
解得：x1＝﹣4，x2＝6．
【点评】本题考查了利用因式分解的方法解一元二次方程，掌握“因式分解法和解方程的基本步骤”是解本题的关键．
17．（10分）已知二次函数y＝x2﹣4x+3．
（Ⅰ）将y＝x2﹣4x+3化成y＝a（x﹣h）2+k的形式：　y＝（x﹣2）2﹣1；　；
（Ⅱ）抛物线与x轴交点坐标为 　（1，0）或（3，0）　；
（Ⅲ）在平面直角坐标系中，画出这个二次函数的图象；
（Ⅳ）当y＜0时，x的取值范围是 　x＜3或x＞1　；
（Ⅴ）当0＜x＜3时，y的取值范围是 　1＜x＜3　．

【分析】（Ⅰ）利用配方法化简即可；
（Ⅱ）将已知二次函数解析式转化为两点式，可以直接得到答案；
（Ⅲ）用“五点法”取值描点连线即可求解；
（Ⅳ）、（Ⅴ）观察函数图象即可求解．
【解答】解：（Ⅰ）y＝x2﹣4x+3＝（x﹣2）2﹣1，
故答案为：y＝（x﹣2）2﹣1；
（Ⅱ）由二次函数y＝x2﹣4x+3＝（x﹣1）（x﹣3）知，该图象与x轴的交点为（1，0）或（3，0），
故答案为：（1，0）或（3，0）；
（Ⅲ）当x＝0时，y＝3；当x＝1时，y＝0；当x＝﹣2时，y＝﹣1；当x＝3时，y＝0；当x＝4时，y＝3，
用上述五点描点连线得到函数图象如下：

（Ⅳ）观察函数图象知，当自变量x的取值范围满足x＜3或x＞1时，y＜0．
故答案是：x＜3或x＞1；
（Ⅴ）观察函数图象知，当1＜x＜3时，y的取值范围是：y＜0．
故答案是1＜x＜3．
【点评】本题考查的是抛物线与x轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．
18．（10分）已知Rt△ABC中，∠ACB＝90°，AC＝4，∠B＝30°，把边AC绕点A逆时针旋转，点C的对应点D落在边AB上．
（Ⅰ）如图①，则线段AD的长为 　4　，旋转角的大小为 　60°　，点D到直线BC的距离为 　2　；
（Ⅱ）点P是直线BC上的一个动点，连接AP，把△ACP绕点A逆时针旋转，使边AC与AD重合，得△ADQ，点Q与点P是对应点．如图②，当点P在边CB上，且CP＝3时，求PQ的长．

【分析】（Ⅰ）先由旋转的性质得AD＝AC＝4，再由直角三角形的性质得AB＝2AC＝8，∠CAB＝60°，过D作DF⊥BC于F，由直角三角形的性质即可得出DF＝BD＝2；
（Ⅱ）先由旋转的性质得△ADQ≌△ACP，则AQ＝AP，∠PAQ＝∠CAD＝60°，再证出△PAQ是等边三角形，得PQ＝AP，然后由勾股定理即可得出答案．
【解答】解：（Ⅰ）由旋转的性质得：AD＝AC＝4，
∵∠ACB＝90°，∠B＝30°，
∴AB＝2AC＝8，∠CAB＝90°﹣30°＝60°，
即旋转角的大小为60°，
过D作DF⊥BC于F，如图①所示：
∵BD＝AB﹣AD＝4，∠B＝30°，
∴DF＝BD＝2，
即点D到直线BC的距离为2，
故答案为：4，60°，2；
（Ⅱ）如图②所示：
∵把△ACP绕点A逆时针旋转，使边AC与AD重合，
∴△ADQ≌△ACP，
∴AQ＝AP，∠PAQ＝∠CAD＝60°，
∴△PAQ是等边三角形，
∴PQ＝AP，
在Rt△ACP中，AP＝＝＝，
∴PQ＝．


【点评】本题是几何变换综合题目，考查了旋转的性质、等边三角形的判定与性质、全等三角形的性质、含30°角的直角三角形的性质、勾股定理等知识；本题综合性强，熟练掌握旋转的性质和含30°角的直角三角形的性质，属于中考常考题型．
19．（10分）如图，抛物线y＝x2+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C．直线y＝x﹣2经过B、C两点，点P是抛物线上一动点．
（1）求抛物线的解析式；
（2）当点P在BC下方运动时，求△BCP面积的最大值．
（3）连接OP，把△OCP沿着y轴翻折，使点P落在P'的位置，四边形CPOP'能否构成菱形，若能，求出点P的坐标，如不能，请说明理由；
（4）把抛物线y＝x2+bx+c向上平移1.5个单位，再向左平移m个单位，使顶点落在△ABC内部，求直接写出点m的取值范围．

【分析】（1）先求出点B，C坐标，再代入抛物线解析式中，即可得出结论；
（2）过点P作PG∥y轴交BC于点G，设P（t，t2﹣t﹣2，则G（t，t﹣2），则PG＝﹣t2+2t，S△BCP＝﹣（t﹣2）2+4，再求解即可；
（3）由翻折得，点P、P'关于y轴对称，可得OC垂直平分PP′，当PP′垂直平分OC时，四边形CPOP'能构成菱形，则点P的纵坐标为﹣1，代入y＝x2﹣x﹣2求出x的值，即可求解；
（4）平移后抛物线的解析式为y＝（x﹣+m）2﹣+1.5，然后求得直线AC的解析式为y＝﹣2x﹣2，由抛物线的顶点在△ABC的内部即可求得m的取值范围．
【解答】解：（1）对于直线y＝x﹣2，
令x＝0，则y＝﹣2，
∴C（0，﹣2），
令y＝0，则0＝x﹣2，
∴x＝4，
∴B（4，0），
将点B，C坐标代入抛物线y＝x2+bx+c中，得，
∴，
∴抛物线的解析式为y＝x2﹣x﹣2；

（2）过点P作PG∥y轴交BC于点G，

设P（t，t2﹣t﹣2，则G（t，t﹣2），
∴PG＝t﹣2﹣t2+t+2＝﹣t2+2t，
∴S△BCP＝×4（﹣t2+2t）＝﹣（t﹣2）2+4，
∴当t＝2时，S△BCP的值最大，最大值为4；

（3）如图，

由翻折得，点P、P'关于y轴对称，
∴OC垂直平分PP′，
当PP′垂直平分OC时，四边形CPOP'能构成菱形，
∴点P的纵坐标为﹣1，
当y＝﹣1时，﹣1＝x2﹣x﹣2，
∴x＝，
∴四边形CPOP'能构成菱形，点P的坐标为（，﹣1）或（，﹣1）；

（4）∵y＝x2﹣x﹣2＝（x﹣）2﹣，
∴平移后抛物线的解析式为y＝（x﹣+m）2﹣+1.5＝（x﹣+m）2﹣，
∴平移后抛物线的顶点坐标为（﹣m，﹣），
y＝x2﹣x﹣2，当y＝0时，x2﹣x﹣2＝0，
∴x＝4或﹣1，
∴A（﹣1，0），C（0，﹣2），
∵设直线AC的解析式y＝kx﹣2，
∴﹣k﹣2＝0，解得k＝﹣2，
∴直线AC的解析式为y＝﹣2x﹣2，
当y＝﹣时，﹣2x﹣2＝﹣，
∴x＝﹣，
∴﹣m＞﹣，
∴m＜；
∵直线BC的解析式为y＝x﹣2，
当y＝﹣时，x﹣2＝﹣，
∴x＝，
∴﹣m＜，
∴m＞；
综上所述，m的取值范围为＜m＜．
【点评】本题是二次函数综合题，考查一次函数的应用、平移变换、翻折变换，菱形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会用数形结合的思想思考问题，属于中考压轴题．