《新高考数学大二轮复习课件》专题二 培优点6 平面向量数量积的最值与范围问题

这是一份《新高考数学大二轮复习课件》专题二 培优点6 平面向量数量积的最值与范围问题，共23页。PPT课件主要包含了跟踪演练，∴P14，因为0≤t≤1等内容，欢迎下载使用。
平面向量的数量积是平面向量的重要内容，求解平面向量数量积的最值与范围问题，要深刻理解数量积的意义，从不同角度对数量积进行转化.
解析　如图，以BC所在直线为x轴，BC的垂直平分线DA为y轴，D为坐标原点建立平面直角坐标系，
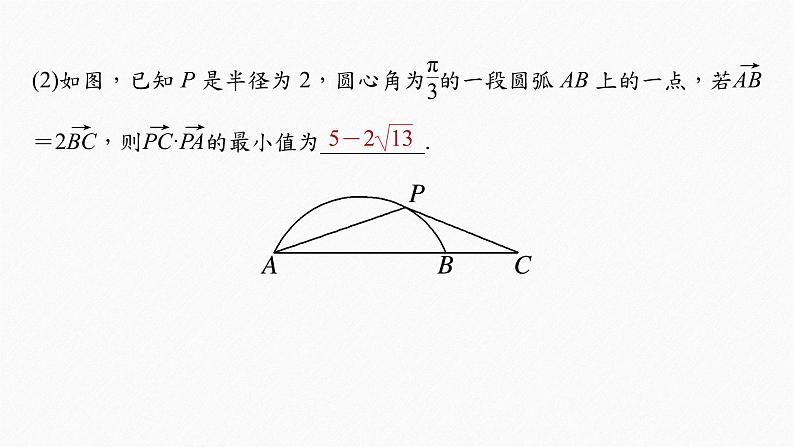
解析　以圆心为坐标原点，平行于AB的直径所在直线为x轴，AB的垂直平分线所在的直线为y轴，建立平面直角坐标系(图略)，
解析　如图，取线段AB的中点M，连接OM，则OM⊥AB，∵A，B是圆x2＋y2＝16上的两个动点，且∠AOB＝120°，
则OM＝2，即M点轨迹为以原点为圆心，以2为半径的圆.
设原点到直线3x＋4y＋25＝0的距离为d，
与数量积有关的最值和范围问题是高考的热点之一，其基本题型是根据已知条件求某个变量的范围、最值，比如向量的模、数量积、夹角、系数的范围等.解决思路是建立目标函数的解析式，转化为求函数(二次函数、三角函数)等的最值或应用基本不等式.同时向量兼顾“数”与“形”的双重身份，所以还有一种思路是数形结合，应用图形的几何性质.
即12(a·b)2＋2a·b－2＝0，整理得(2a·b＋1)(3a·b－1)＝0，
解析　建立如图所示的平面直角坐标系，
4.已知a，b是单位向量，a·b＝0，若向量c满足|c－a＋b|＝1，则|c－b|的取值范围是________________.
解析　由a，b是单位向量，且a·b＝0，则可设a＝(1,0)，b＝(0,1)，c＝(x，y).∵向量c满足|c－a＋b|＝1，∴|(x－1，y＋1)|＝1，
即(x－1)2＋(y＋1)2＝1，它表示圆心为C(1，－1)，半径为r＝1的圆，