江苏省泰州市姜堰区四校联考2022-2023学年八年级上学期10月月考数学试卷(解答案)

这是一份江苏省泰州市姜堰区四校联考2022-2023学年八年级上学期10月月考数学试卷(解答案)，共13页。试卷主要包含了选择题．，填空题．，解答题．等内容，欢迎下载使用。
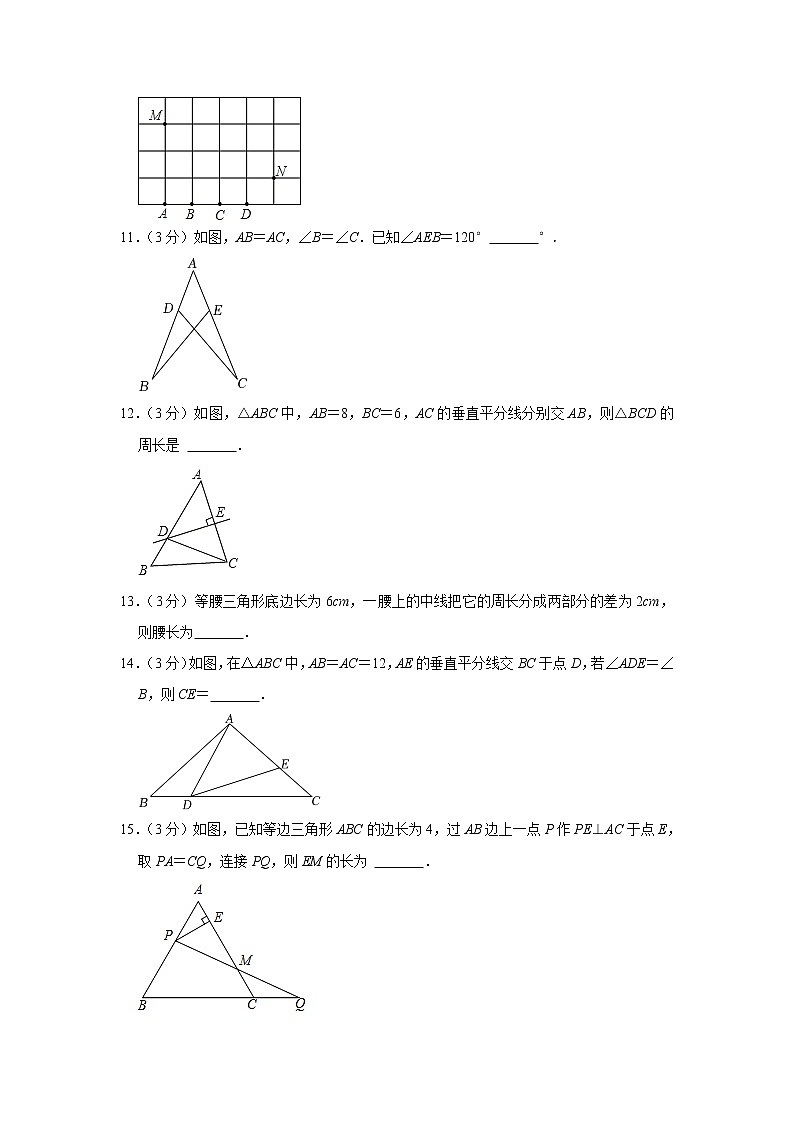
2022-2023学年江苏省泰州市姜堰区四校联考八年级（上）月考数学试卷（10月份）一、选择题（本大题共6小题，每小题3分，共18分）．1．（3分）2022年2月4日至20日，第24届冬奥会在北京和张家口举办，北京是唯一举办过夏季和冬季奥运会的城市，其中是轴对称图形的是（　　）A． B． C． D．2．（3分）如图，在等边△ABC中，AB＝4cm，点E在BC的延长线上，且∠E＝30°（　　）A．1cm B．2cm C．3cm D．4cm3．（3分）如图，在方格纸中，以AB为一边作△ABP，在方格的格点中找出符合条件的P点（不与点A，B，C重合），则点P有（　　）A．1个 B．2个 C．3个 D．4个4．（3分）如图，在等腰三角形ABC中，AB＝AC，直线MN垂直平分边AC，分别交AB，E，则∠BCD＝（　　）A．10° B．15° C．20° D．25°5．（3分）如图，△ABC的三边AB，BC，20，25，则S△ABO：S△BCO：S△CAO等于（　　）A．1：1：1 B．1：2：3 C．2：3：4 D．3：4：56．（3分）如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，再分别以M、N为圆心，大于，两弧交于点P，连结AP并延长交BC于点D，②点D在AB的垂直平分线上，③AB＝2AC△DAB＝2S△DAC，其中正确的个数是（　　）A．1 B．2 C．3 D．4二、填空题（本大题共10小题，每小题3分，共30分）．7．（3分）如果2m×4m＝215，那么m＝　   　．8．（3分）冠状病毒最先是1937年从鸡身上分离出来，病毒颗粒的平均直径为0.00000011m，用科学记数法表示这个数是　   　．9．（3分）某电梯中一面镜子正对楼层显示屏，显示屏中显示的是电梯所在楼层号和电梯运行方向．当电梯中镜子如图显示时，电梯所在楼层号为 　   　．10．（3分）如图，桌球的桌面上有M，N两个球，反弹一次后击中N球，则A，B，C，D，可以反弹击中N球的是 　   　点．11．（3分）如图，AB＝AC，∠B＝∠C．已知∠AEB＝120°　   　°．12．（3分）如图，△ABC中，AB＝8，BC＝6，AC的垂直平分线分别交AB，则△BCD的周长是 　   　．13．（3分）等腰三角形底边长为6cm，一腰上的中线把它的周长分成两部分的差为2cm，则腰长为　   　．14．（3分）如图，在△ABC中，AB＝AC＝12，AE的垂直平分线交BC于点D，若∠ADE＝∠B，则CE＝　   　．15．（3分）如图，已知等边三角形ABC的边长为4，过AB边上一点P作PE⊥AC于点E，取PA＝CQ，连接PQ，则EM的长为 　   　．16．（3分）如图，△ABC是等边三角形，直线MN⊥AC于点C，以AD为边向右作等边△ADE，连接CE，则CE的最小值是 　   　．三、解答题（本大题共10小题，共102分）．17．（10分）计算：（1）16×2﹣3+（）0÷（）2；（2）a2•a4+（2a3）2．18．（10分）（1）解方程组；（2）解不等式组．19．（8分）先化简，再求值：（x﹣2）2﹣4x（x﹣1）+（2x+1）（2x﹣1），其中x＝2．20．（8分）如图，在长度为1个单位长度的小正方形组成的正方形网格中，△ABC的三个顶点A、B、C都在格点上．（1）在图中画出与△ABC关于直线l成轴对称的△A1B1C1；（2）在直线l上找出一点P，使得|PA﹣PC1|的值最大，该最大值为 　   　（保留作图痕迹并标上字母P）（3）在正方形网格中存在 　   　个格点，使得该格点与B、C两点构成以BC为底边的等腰三角形．21．（8分）已知：如图，∠A＝∠D，∠B＝∠E，求证：AC＝DF．22．（10分）如图，△ABC≌△DBE，点A、D、C在同一条直线上，∠C＝35°，求∠DBC的度数．23．（10分）如图，在△ABC中，AF平分∠BAC，交AC于点D，∠B＝75°，求∠C的度数．24．（12分）如图，已知△ABC，AD是∠BAC的角平分线，DF⊥AC于点F，连接EF交AD于点G．（1）求证：AD垂直平分EF；（2）若AB+AC＝10，DE＝3，求△ABC的面积．25．（12分）在△ABC中，AB、AC的垂直平分线分别交BC于点E、F． （1）如图，当∠B＝∠C＝20°时，求∠EAF的度数；（2）如图，AB≠AC，且90°＜∠BAC＜180°．①若∠BAC＝130°，则∠EAF＝　   　°；若∠BAC＝n°，则∠EAF＝　   　°；②当∠BAC＝　   　°时，AE⊥AF；③若BC＝a，求△AEF的周长．（用含a的式子表示）26．（14分）如图1，在等边三角形ABC中，AD⊥BC于D，AD与CE相交于点O．（1）求证：OA＝2DO；（2）如图2，若点G是线段AD上一点，CG平分∠BCE，GF交CE所在直线于点F．求证：GB＝GF．（3）如图3，若点G是线段OA上一点（不与点O重合），连接BG，边GF交CE所在直线于点F．猜想：OG，OF、OA三条线段之间的数量关系
2022-2023学年江苏省泰州市姜堰区四校联考八年级（上）月考数学答案一、选择题（本大题共6小题，每小题3分，共18分）．1．D．2．B．3．C．4．B．5．D．6．D．二、填空题（本大题共10小题，每小题3分，共30分）．7．58．1.8×10﹣7．9．15．10．点D．11．60．12．14．13．4cm或8cm．14．4．15．2．16．3．三、解答题（本大题共10小题，共102分）．17．解：（1）16×2﹣3+（）0÷（）2＝16×+1÷＝2+5×4＝2+7＝6；（2）a2•a3+（2a3）2＝a6+4a2＝5a6．18．解：（1）将x＝3y代入﹣y＝﹣7y﹣y＝﹣5，解得y＝4，将y＝4代入x＝5y，得：x＝12，所以方程组的解为；（2）解不等式2x+6≤3（x+2），得：x≥﹣8，解不等式＜，得：x＜3，则不等式组的解集为﹣1≤x＜2．19．解：原式＝x2﹣4x+2﹣4x2+4x+4x2﹣4＝x2+3，当x＝7时，原式＝4+3＝6．20．解：（1）如图所示，△A1B1C5即为所求；（2）如图所示，点P即为所求1|的值最大，最大值为线段A1C的长，A4C＝＝5，（3）如图，在正方形网格中存在4个格点、C两点构成以BC为底边的等腰三角形，故答案为：421．证明：∵BF＝CE，∴BF+CF＝CE+CF，即BC＝EF，在△ABC与△DEF中，，∴△ABC≌△DEF（AAS），∴AC＝DF．22．解：∵△ABC≌△DBE，∴AB＝BD，∴∠A＝∠BDA＝60°，∵∠BDA＝∠C+∠DBC，∠C＝35°，∴∠DBC＝60°﹣35°＝25°，故∠DBC的度数为25°．23．解：∵DE是AC的垂直平分线，∴EA＝EC，∴∠EAC＝∠C，∵∠FAE＝15°，∴∠FAC＝∠EAC+15°＝∠C+15°，∵AF平分∠BAC，∴∠BAE＝∠FAC＝∠C+15°，∵∠B+∠BAC+∠C＝180°，∴75°+∠C+15°+∠C+15°+∠C＝180°，解得：∠C＝25°．24．（1）证明：∵DE⊥AB，DF⊥AC，∴∠DEA＝∠DFA＝90°，∵AD是∠BAC的角平分线，∴∠EAD＝∠FAD，在△AED和△AFD中，，∴△AED≌△AFD（AAS），∴AE＝AF，∵AD是∠BAC的角平分线，∴AG⊥EF，EG＝FG，∴AD垂直平分EF；（2）解：∵AD是∠BAC的角平分线，DE⊥AB于点E，∴DE＝DF，∵DE＝3，∴DF＝3，∵AB+AC＝10，∴△ABC的面积＝＝＝15．25．解：（1）∵DE垂直平分AB，GF垂直平分AC，∴BE＝AE，AF＝CF．∴∠B＝∠BAE＝20°，∠C＝∠CAF＝20°．∴∠BAE+∠CAF＝40°．∵∠B＝∠C＝20°，∴∠BAC＝180°﹣∠B﹣∠C＝140°．∴∠EAF＝∠BAC﹣（∠BAE+∠CAF）＝140°﹣40°＝100°．（2）①由（1）得：∠B＝∠BAE，∠C＝∠CAF．∵∠BAC＝130°，∴∠B+∠C＝180°﹣∠BAC＝50°．∴∠BAE+∠CAF＝50°．∴∠EAF＝∠BAC﹣（∠BAE+∠CAF）＝130°﹣50°＝80°．若∠BAC＝n°，∴∠B+∠C＝180°﹣∠BAC＝180°﹣n°．∴∠BAE+∠CAF＝180°﹣n°．∴∠EAF＝∠BAC﹣（∠BAE+∠CAF）＝n°﹣（180°﹣n°）＝2n°﹣180°．故答案为：80，2n﹣180．②由（1）可知：当∠BAC＝n°，则∠EAF＝6n°﹣180°．∵AE⊥AF，∴∠EAF＝90°．∴2n°﹣180°＝90°．∴n°＝135°．∴当∠BAC＝135°时，AE⊥AF．故答案为：135．③∵DE垂直平分AB，GF垂直平分AC，∴BE＝AE，AF＝CF．∵BC＝BE+EF+CF＝a，∴BC＝AE+EF+AF＝a．∴△AEF的周长为a．26．（1）证明：∵△ABC为等边三角形，∴AB＝BC＝AC，∠BAC＝∠ACB＝60°，∵AD⊥BC，CE⊥AB，∴AD平分∠BAC，CE平分∠ACB，∴∠OAC＝∠OAB＝∠OCA＝∠OCB＝30°，∴OA＝OC，在Rt△OCD中，∠ODC＝90°，∴OC＝2OD，∴OA＝2OD；（2）证明：∵AB＝AC＝BC，AD⊥BC，∴BD＝CD，∴BG＝CG，∴∠GCB＝∠GBC，∵CG平分∠BCE，∴∠FCG＝∠BCG＝∠BCF＝15°，∴∠BGC＝150°，∵∠BGF＝60°，∴∠FGC＝360°﹣∠BGC﹣∠BGF＝150°，∴∠BGC＝∠FGC，在△CGB和△CGF中，，∴△CGB≌△CGF（ASA），∴GB＝GF；（3）解：OF＝OG+OA．理由如下：连接OB，在OF上截取OM＝OG，∵CA＝CB，CE⊥AB，∴AE＝BE，∴OA＝OB，∴∠OAB＝∠OBA＝30°，∴∠AOB＝120°，∠AOM＝∠BOM＝60°，∵OM＝OG，∴△OMG是等边三角形，∴GM＝GO＝OM，∠MGO＝∠OMG＝60°，∵∠BGF＝60°，∴∠BGF＝∠MGO，∴∠MGF＝∠OGB，∵∠GMF＝120°，∴∠GMF＝∠GOB，在△GMF和△GOB中，，∴△GMF≌△GOB（ASA），∴MF＝OB，∴MF＝OA，∵OF＝OM+MF，∴OF＝OG+OA．