山西省临汾市古县2022年九年级上学期期末数学试题及答案

 九年级上学期期末数学试题

一、单选题

1．下列各式中，是二次根式的是（　　）

A． B． C． D．

2．若关于的一元二次方程中，是投掷骰子所得的数字（1，2，3，4，5，6），则该方程有两个不相等的实数根的概率为（　　）

A． B． C． D．

3．已知Rt△ABC中，∠BAC＝90°，过点A作一条直线，使其将△ABC分成两个相似的三角形．观察下列图中尺规作图痕迹，作法错误的（　　）

A． B．

C． D．

4．用配方法将二次函数y=x2﹣8x﹣9化为y=a（x﹣h）2+k的形式为（　　）  

A．y=（x﹣4）2+7 B．y=（x+4）2+7

C．y=（x﹣4）2﹣25 D．y=（x+4）2﹣25

5．在求解一元二次方程﹣2x2+4x+1＝0的两个根x1和x2时，某同学使用电脑软件绘制了如图所示的二次函数y＝﹣2x2+4x+1的图象，然后通过观察抛物线与x轴的交点，该同学得出﹣1＜x1＜0，2＜x2＜3的结论，该同学采用的方法体现的数学思想是（　　） 

A．类比 B．演绎 C．数形结合 D．公理化

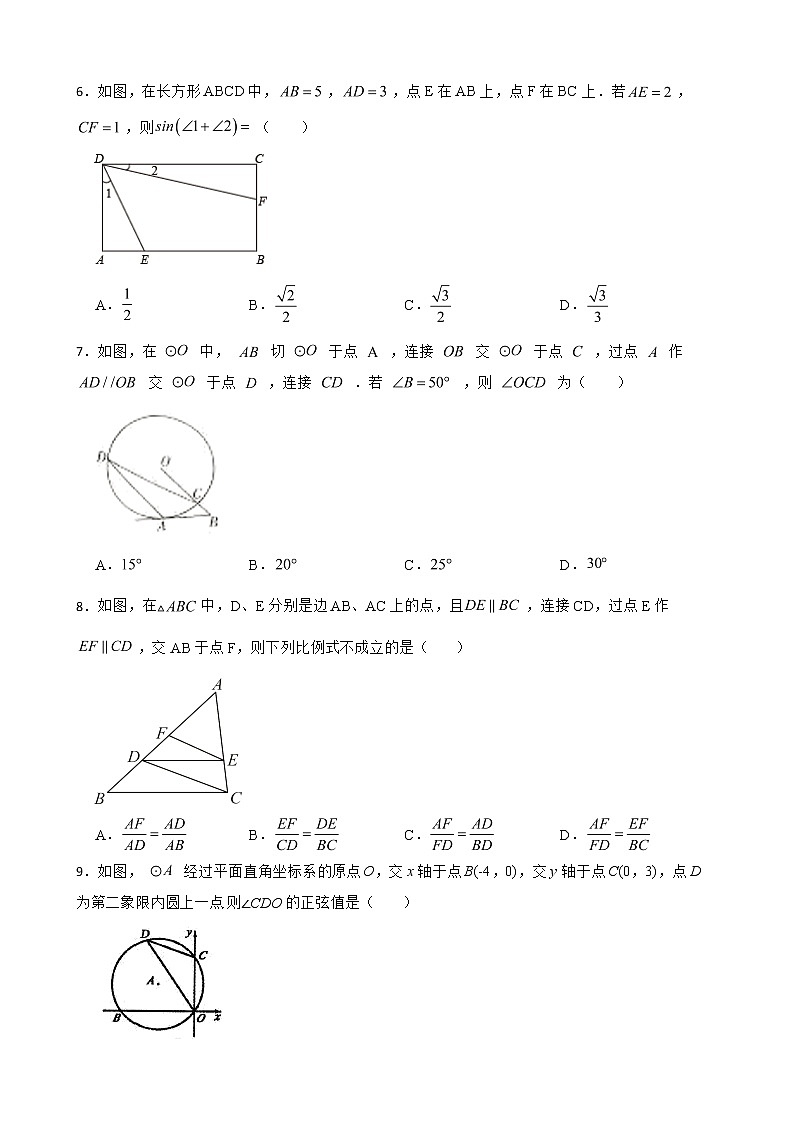
6．如图，在长方形ABCD中，，，点E在AB上，点F在BC上．若，，则（　　）

A． B． C． D．

7．如图，在 中， 切 于点 ，连接 交 于点 ，过点 作 交 于点 ，连接 ．若 ，则 为（　　） 

A． B． C． D．

8．如图，在中，D、E分别是边AB、AC上的点，且，连接CD，过点E作，交AB于点F，则下列比例式不成立的是（　　）

A． B． C． D．

9．如图， 经过平面直角坐标系的原点O，交x轴于点B(-4，0)，交y轴于点C(0，3)，点D为第二象限内圆上一点.则∠CDO的正弦值是（　　） 

A． B． C． D．

10．如图，抛物线与轴相交于，两点，与轴相交于点，点在抛物线上，且.与轴相交于点，过点的直线平行于轴，与抛物线相交于，两点，则线段的长为（　　）

A． B． C． D．

二、填空题

11．计算的结果　     　．

12．若，β均为锐角，且|sin﹣|+（﹣tanβ）2＝0，则+β＝　     　．

13．已知⊙与⊙的半径分别是方程的两根，且，若这两个圆相切，则＝　           　．

14．教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）之间的关系为 ，由此可知铅球推出的距离是　     　m.

15．如图，在▱ABCD中，对角线AC，BD相交于点O，在BA的延长线上取一点E，连接OE交AD于点F.若CD＝5，BC＝8，AE＝2，则AF＝　     　．

三、解答题

16．  

（1）计算：；

（2）解方程：．

17．如图，已知在平面直角坐标系中，的三个顶点坐标分别是，，．

（1）将向右平移4个单位长度后得到，请画出；

（2）画出关于轴对称的；

（3）连接，求的值．

18．2020年5月13日，共青团中央维护青少年权益部、中国互联网络信息中心（CNNIC）联合发布《2019年全国未成年人互联网使用情况研究报告》．下面是根据此报告得到的统计图．

（1）由统计图可知未成年网民中工作日玩手机游戏的日均时长超过2小时的约占　     　%．

（2）小文根据报告整理了“初中生上网经常从事各类活动的百分比及排行榜（前五）”，如下表．

小文发现，这些活动所占百分比之和远远超过100%，请你解释其中的原因．

（3）小文关注了“人民日报”“共青团中央”“新华社”“中科院之声”4个微信公众号（依次记为A，B，C，D）．他每天早晨会从这4个公众号中随机选择一个，浏览最新信息．求小文连续两天浏览同一个公众号的概率．

19．如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠BCD＝∠A.

（1）求证：CD是⊙O的切线；

（2）若⊙O的半径为3，CD＝4，求BD的长.

20．阅读下列材料，并完成相应任务．

黄金分割

天文学家开普勒把黄金分割称为神圣分割，并指出，毕达哥拉斯定理（勾股定理）和黄金分割“是几何中的双宝，前者好比黄金，后者堪称珠玉”．历史上最早正式在书中使用“黄金分割”这个名称的是欧姆.19世纪以后，“黄金分割”的说法逐渐流行起来，黄金分割被广泛应用于建筑等领域．黄金分割指把一条线段分为两部分，使其中较长部分与线段总长之比等于较短部分与较长部分之比，该比值为．用下面的方法（如图（1））就可以作出已知线段AB的黄金分割点H；

①以线段AB为边作正方形ABCD；

②取AD的中点E，连接EB；

③延长DA到点F，使；

④以线段AF为边作正方形AFGH，点H就是线段AB的黄金分割点．

以下是证明点H就是线段AB的黄金分割点的部分过程．

证明：设正方形ABCD的边长为1，则．

∵点E为AD的中点，∴．

在中，，∴，

∴．……

任务：

（1）补全题中的证明过程．

（2）如图（2），点C为线段AB的黄金分割点（），分别以AC，BC为边在线段AB同侧作正方形ACDE和矩形CBFD，连线BD，BE．求证：．

（3）如图（3），在正五边形ABCDE中，对角线AD，AC与EB分别交于点M，N．求证：点M是AD的黄金分割点．

21．垃圾分类作为一个公共管理的综合系统工程，需要社会各个层面共同发力，今年5月，太原市20个小区实施“撤桶并站、定时定点、分类投放，桶边督导”，掀起了垃圾分类的新风尚．某超市计划定制一款家用分类垃圾桶，独家经销．生产厂家给出如下定制方案：不收设计费，定制不超过200套时，每套费用60元；超过200套后，超出的部分8折优惠．已知该超市定制这款垃圾桶的平均费用为56元1套．

（1）该超市定制了这款垃圾桶多少套？

（2）超市经过市场调研发现：当此款垃圾桶售价定为80元/套时，平均每天可售出20套；售价每降低1元，平均每天可多售出2套．当售价下降多少元时，可使该超市平均每天销售此款垃圾桶的利润最大？．

22．如图，中，，是的内切圆，D，E，F是切点．

（1）求证：四边形ODCE是正方形；

（2）如果，，求内切圆的半径．

23．下图是二次函数的图象，其顶点坐标为．

（1）求出图象与轴的交点，的坐标；

（2）在二次函数的图象上是否存在点，使？若存在，求出点的坐标；若不存在，请说明理由；

（3）将二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线与此图象有两个公共点时，的取值范围．

答案解析部分

1．【答案】A

2．【答案】A

3．【答案】B

4．【答案】C

5．【答案】C

6．【答案】B

7．【答案】B

8．【答案】D

9．【答案】A

10．【答案】D

11．【答案】2

12．【答案】90°

13．【答案】0或2或2或0

14．【答案】10

15．【答案】

16．【答案】（1）解：原式，

，

．

（2）解：将原方程化成一般形式，得，

因为，

所以，

整理，得，

所以，，．

17．【答案】（1）解：如图，△A1B1C1为所作；

（2）解：如图，△A2B2C2为所作；

（3）解：连接，

，

，

，

∵，

∴，且，

∴是等腰直角三角形，且∠=90，

∴∠=45，

∴．

18．【答案】（1）12.5

（2）解：收集数据时，对于调查项目没有要求单项选择，所以，各个项目数据有重叠，各数据所占的百分比之和就会超过100%；

（3）解：画树状图如图所示，共有16种等可能的结果，其中连续两天浏览同一个公众号的结果有4种，∴“连续两天浏览同一个公众号“的概率P＝．

19．【答案】（1）证明：如图，连接OC.

∵AB是⊙O的直径，C是⊙O上一点，

∴∠ACB=90°，即∠ACO+∠OCB=90°.

∵OA=OC，∠BCD=∠A，

∴∠ACO=∠A=∠BCD，

∴∠BCD+∠OCB=90°，即∠OCD=90°，

∴CD是⊙O的切线

（2）解：在Rt△OCD中，∠OCD=90°，OC=3，CD=4，

∴OD= =5，

∴BD=OD﹣OB=5﹣3=2

20．【答案】（1）证明：设正方形ABCD的边长为1，则．

∵点E为AD的中点，

∴．

在中，，

∴，

∴．

∵四边形AFGH为正方形，

∴，

∴，

∴点H是线段AB的黄金分割点．

（2）证明∶设AC的长为1，

∵点C为线段AB的黄金分割点（），

∴，

∴，

∵四边形ACDE是正方形，四边形CBFD是矩形，

∴，∠A=∠BCD=90°，

∴， ，

∴ ，

∴；

（3）证明：在正五边形ABCDE中，AE=DE=AB，，

∴∠ABE=∠AEB=∠DAE=∠ADE=36°，

∴∠DEM=∠AED-∠AEB=72°，AM=EM，

∴∠DME=72°，

∴∠DME=∠DEM，

∴DM=DE=AE，

设DM=1，

∵∠AEM=∠ADE，∠EAM=∠EAD，

∴△AEM∽△ADE，

∴，即，

解得：或（舍去）．

∴，

即点M是AD的黄金分割点．

21．【答案】（1）解：设该超市定制了这款垃圾桶套．

因为56<60，所以．

根据题意，得．

解，得．

答：该超市定制这款垃圾桶300套．

（2）解：设售价下降元，平均每天销售此款垃圾桶的利润为元．

根据题意，得．

整理，得．

因为，且，

所以，当时，有最大值．

答：售价下降7元时，平均每天销售此款垃圾桶的利润最大．

22．【答案】（1）证明：∵BC，AC分别切于点D，E，

∴，，

又∵，

∴四边形ODCE是矩形，

又∵，

∴矩形ODCE是正方形．

（2）解：设的半径为r，

∵四边形ODCE是正方形，

∴，

在中，，

∴，，

∵与各边相切于点D，E，F，

∴，，

又∵，

∴，解得

∴内切圆的半径是1．

23．【答案】（1）解：因为是二次函数的顶点坐标，

所以，

令，

解之得，．

∴，两点的坐标分别为，；

（2）解：在二次函数的图象上存在点，使，

设，

则，

又∵，

∴．

∵二次函数的最小值为，

∴．

当时，或．

故点坐标为或；

（3）解：如图，

当直线经过时，可得，又因为，

故可知在的下方，

当直线经过点时，，则，

由图可知正确的的取值范围为时，直线与此图象有两个公共点．