2022-2023学年河南省郑州外国语中学八年级（上）期中数学试卷（含解析）

这是一份2022-2023学年河南省郑州外国语中学八年级（上）期中数学试卷（含解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年河南省郑州外国语中学八年级（上）期中数学试卷  第I卷（选择题） 一、选择题（本大题共5小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）在下列实数中，属于无理数的是(    )A.  B.  C.  D. 下列条件中，不能判定是直角三角形的是(    )A.  B. ：：：：
C.  D. ：：：：点，在一次函数的图象上，与的大小关系是(    )A.  B.  C.  D. “今有人盗库绢，不知所失几何．但闻草中分绢，人得六匹，盈六匹；人得七匹，不足七匹，问人、绢各几何？选自孙子算经”大意为：有盗贼窃去库存的绸缎，不知究竟窃去多少．有人在草丛中听到这帮盗贼分赃的情况．如果每个盗贼分得匹，就多出匹；如果每个盗贼分得匹，就缺少匹．盗贼有几人？失窃的绸缎有几匹？设盗贼有人，失窃的绸缎有匹，根据题意可列方程组为(    )A.  B.  C.  D. 李老师童心未泯，拿着如图的密码表玩听声音猜动物的游戏，若听到“咚咚咚咚，咚咚，咚咚咚咚”表示的动物是“狗”，那么若听到“咚咚咚，咚咚咚咚咚，咚咚咚咚”时，表示的动物是(    )
 A. 狐狸 B. 牛 C. 蜜蜂 D. 猫第II卷（非选择题） 二、填空题（本大题共5小题，共20.0分）的立方根是______．已知变量与满足一次函数关系，且随的增大而减小，若其图象与轴的交点坐标为，请写出一个满足上述要求的函数关系式______．某商场销售，，，四种商品，它们的单价依次是元，元，元，元．某天这四种商品销售数量的百分比如图所示，则这天销售的四种商品的平均单价是______元．
 李老师和“几何小分队”的队员们在学习数学史时，发现了一个著名的“希波克拉蒂月牙问题”：如图在中，，，，分别以的各边为直径作半圆，则图中两个“月牙”即阴影部分面积为______．如图，在平面直角坐标系中，长方形的边、分别在轴、轴上，，点在边上，将长方形沿折叠，若点的对应点恰好是边的三等分点，则点的坐标是______．
   三、解答题（本大题共6小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）本小题分
计算：；
解方程组：．本小题分
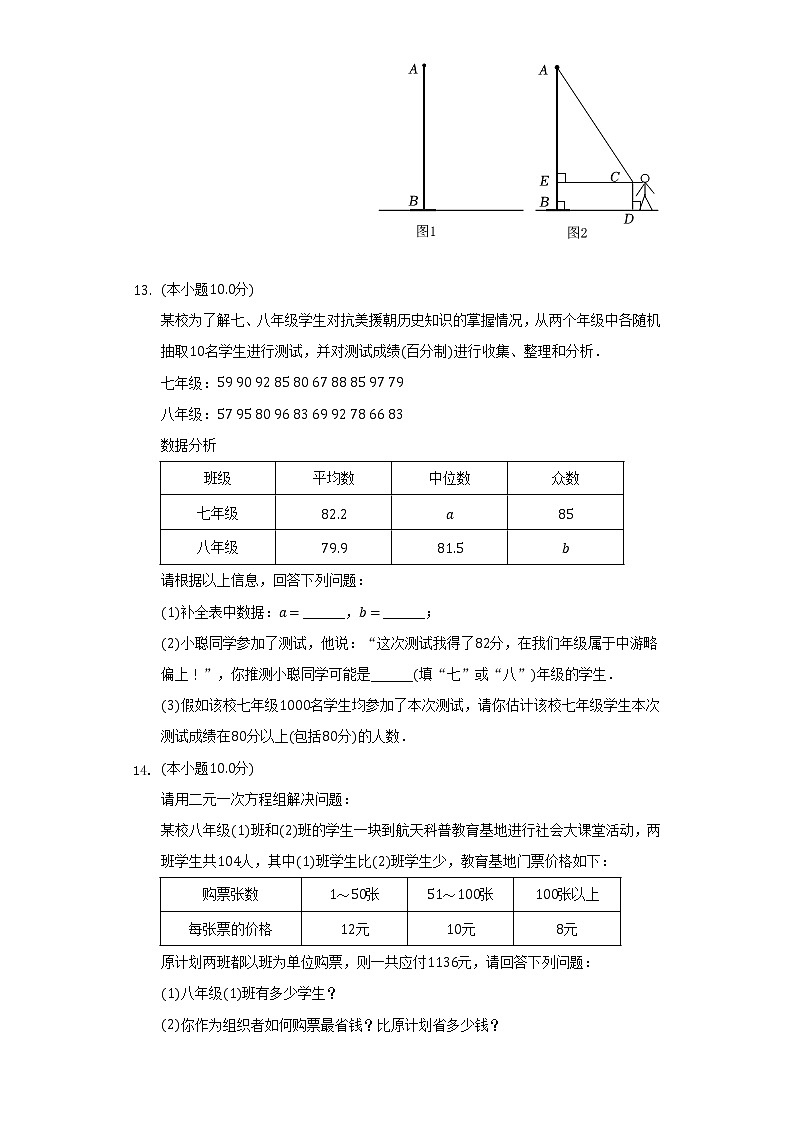
学过勾股定理后，李老师和“几何小分队”的队员们到操场上测量旗杆高度，得到如下信息：
测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长米如图；
当将绳子拉直时，测得此时拉绳子的手到地面的距离为米，到旗杆的距离为米如图．
根据以上信息，求旗杆的高度．
本小题分
某校为了解七、八年级学生对抗美援朝历史知识的掌握情况，从两个年级中各随机抽取名学生进行测试，并对测试成绩百分制进行收集、整理和分析．
七年级：
八年级：
数据分析班级平均数中位数众数七年级八年级请根据以上信息，回答下列问题：
补全表中数据：______，______；
小聪同学参加了测试，他说：“这次测试我得了分，在我们年级属于中游略偏上”，你推测小聪同学可能是______填“七”或“八”年级的学生．
假如该校七年级名学生均参加了本次测试，请你估计该校七年级学生本次测试成绩在分以上包括分的人数．本小题分
请用二元一次方程组解决问题：
某校八年级班和班的学生一块到航天科普教育基地进行社会大课堂活动，两班学生共人，其中班学生比班学生少，教育基地门票价格如下：购票张数张张张以上每张票的价格元元元原计划两班都以班为单位购票，则一共应付元，请回答下列问题：
八年级班有多少学生？
你作为组织者如何购票最省钱？比原计划省多少钱？本小题分
李老师和“函数小分队”的队员们根据学习函数的经验，对函数的图象和性质进行了探究，探究过程如下：
在自变量的取值范围内，与的几组对应值如下表：其中______；在平面直角坐标系中，画出该函数的图象，并回答以下问题：根据该函数图象写出一条性质：______；
已知函数的图象与函数的图象关于轴对称，请在图中画出函数的图象，并结合图象直接写出直线与函数图象的交点坐标．
本小题分
如图，在平面直角坐标系中，直线与轴，轴分别交于，两点，点为直线上一点，直线过点．
求和的值；
直线与轴交于点，动点在轴上．
若的面积为，求点坐标；
是否存在点使为等腰三角形，若存在，直接写出点坐标；若不存在，请说明理由．

答案和解析 1.【答案】 【解析】解：，，是有理数，
是无理数，
故选：．
分别根据无理数、有理数的定义即可判定选择项．
本题主要考查了无理数的知识，掌握无理数的定义是关键．
 2.【答案】 【解析】解：、，，
，
为直角三角形，故此选项不合题意；
B、设，，，
，
解得：，
则，
不是直角三角形，故此选项符合题意．
C、，即，
，
能构成直角三角形，故此选项不符合题意；
D、，
能构成直角三角形，故此选项不符合题意；
故选：．
根据三角形内角和定理可分析出、的正误；根据勾股定理逆定理可分析出、的正误．
本题考查勾股定理的逆定理的应用．正确记忆判断三角形是否为直角三角形的方法是解题关键．
 3.【答案】 【解析】解：，
随的增大而增大，
又点和点是一次函数图象上的两点，且，
．
故选：．
由，利用一次函数的性质可得出随的增大而增大，结合，即可得出．
本题考查了一次函数的性质，牢记“，随的增大而增大；，随的增大而减小”是解题的关键．
 4.【答案】 【解析】解：每个盗贼分得匹，就多出匹，
；
每个盗贼分得匹，就缺少匹，
．
根据题意可列方程组为．
故选：．
根据“每个盗贼分得匹，就多出匹；每个盗贼分得匹，就缺少匹”，即可得出关于，的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．
 5.【答案】 【解析】解：由题意知，咚咚咚咚对应，咚咚对应，咚咚咚咚对应．
咚咚咚对应，表示；咚咚咚咚咚对应，表示；咚咚咚咚对应，表示．
此时，表示的动物是猫．
故选：．
根据点的坐标解决此题．
本题主要考查点的坐标，熟练掌握点的坐标的表示方法与意义是解决本题的关键．
 6.【答案】 【解析】解：因为，
所以
故答案为：．
根据立方根的定义求解即可．
此题主要考查了立方根的定义，求一个数的立方根，应先找出所要求的这个数是哪一个数的立方．由开立方和立方是互逆运算，用立方的方法求这个数的立方根．注意一个数的立方根与原数的符号相同．
 7.【答案】答案不唯一 【解析】解：由与满足一次函数关系，且随的增大而减小，则，
其图象与轴的交点坐标为，
，
满足上述要求的函数关系式可以为：答案不唯一．
故答案为：答案不唯一．
直接利用一次函数的性质结合其增减性进而得出答案．
此题主要考查了一次函数的性质，正确掌握一次函数的性质是解题关键．
 8.【答案】 【解析】解：这天销售的四种商品的平均单价是：
元，
故答案为：．
根据加权平均数定义即可求出这天销售的四种商品的平均单价．
本题考查了加权平均数、扇形统计图，解决本题的关键是掌握加权平均数的定义．
 9.【答案】 【解析】解：由勾股定理得：，
则



，
故答案为：．
根据勾股定理得到，再根据扇形面积公式计算，得到答案．
本题考查的是勾股定理、扇形面积计算，掌握勾股定理和扇形面积公式是解题的关键．
 10.【答案】或 【解析】解：由题意知点是的三等分点，分两种情况：
若时，，，如图，

将该矩形沿折叠，点恰好落在处，
，
，
四边形是矩形，
．
设，则，
由题意可得，，
，，
，
解得，，
；
若时，，，如图，

将该矩形沿折叠，点恰好落在处，
，
，
四边形是矩形，
．
设，则，
由题意可得，，
，，
，
解得，，
，
解得，，
；
综上所述，点的坐标为或；
故答案为：或；
分两种情况画出图形，由折叠的性质及勾股定理可求出答案．
本题考查勾股定理的应用，矩形的性质、翻折变化、坐标与图形变化对称，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
 11.【答案】解：原式
；
，
，得，
解得，
把代入，得，
故原方程组的解为． 【解析】利用乘方的定义，绝对值的定义以及零指数幂的定义计算即可；
方程组利用加减法求解即可．
本题考查了实数的运算以及解二元一次方程组，掌握相关运算法则以及消元的方法是解答本题的关键．
 12.【答案】解：设，则，，根据题意得：
在中，根据勾股定理得：，
，
．
答：旗杆的高度为米． 【解析】设，在中根据勾股定理列方程求解即可．
本题考查了勾股定理的应用，熟练掌握勾股定理的相关知识并在直角三角形中正确运用是解题的关键．
 13.【答案】    八 【解析】解：因为将七年级对抗美援朝历史知识的掌握情况成绩从小到大排列得：，，，，，，，，，，
中间的数是，，所以中位数，
因为八年级数据中，数据出现两次，出现次数最多，所以这组数据的众数是，即的值为，
故答案为：，．

推测小聪同学可能是八年级的学生．
因为小聪的分数在年级属于中游略偏上，而，即小聪的分数大于八年级的中位数，所以成绩在中游略偏上，
故答案为：八．

由原数据可得七年级分以上包括分的同学有人，
全校学生本次测试成绩在分以上包括分的人数有人，
估计该校七年级学生本次测试成绩在分以上包括分的人数约为人．
根据中位数、众数的定义直接求解即可；
根据中位数的定义判断即可；
先求出七年级学生本次测试成绩在分以上的人数，再用乘以七年级学生本次测试成绩在分以上的人数所占的比例即可．
本题考查了统计表、中位数、众数等知识，熟练掌握中位数、众数的定义，用样本估计总体等知识是解答此题的关键．
 14.【答案】解：设八年级班有人，则八年级班有人，
，
，，
，
解得，，
答：八年级有人；
两个班一起购票最省钱，
元，
即可以节省元． 【解析】根据表格中的数据和两个班人数之间的关系可以列出相应的方程，从而可以得到八年级班的人数；
根据表格中的数据和中的结果，可知两个班一起购买最省钱，从而可以求得可以省多少钱．
本题考查一元一次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答．
 15.【答案】  当时，随的增大而增大 【解析】解：当时，，
故答案为：；


当时，随的增大而增大；
函数的图象与函数的图象关于轴对称，
，

直线与函数图象的交点为．
将代入中即可求的值；
画出函数图象，通过观察函数图象直接求解即可；
求出，再画出函数的图象，根据函数图象写出交点坐标即可；
本题考查一次函数的图象及性质，熟练掌握一次函数的图象及性质，能够准确地画出函数图象，掌握图象对称的性质是解题的关键．
 16.【答案】解：将点代入，
，
解得，
将点代入，
，
解得；
中，令，则，
，
中，令，则，
，
，
，
，
或；
存在点使为等腰三角形，理由如下：
设，
，，，
当时，，
解得，
；
当时，，
解得或，
或；
当时，，
解得或舍去，
；
综上所述：点坐标为或或或． 【解析】分别将点代入，中，即可求、的值；
求出点坐标，由，求出的长，即可求点坐标；
设，分别求出，，，再由等腰三角形边的关系，分三种情况分别求点坐标即可．
本题考查一次函数的图象及性质，熟练掌握一次函数的图象及性质，等腰三角形的性质，分类讨论是解题的关键．