2021-2022学年河北省秦皇岛市卢龙县九年级（上）期末数学试卷（含解析）

2021-2022学年河北省秦皇岛市卢龙县九年级（上）期末数学试卷

第I卷（选择题）

一、选择题（本大题共14小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）

1. 一元二次方程根的情况是(    )

A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定

2. 下列说法正确的是(    )

A. 长度相等的弧是等弧
B. 圆既是轴对称图形，又是中心对称图形
C. 弧是半圆
D. 三点确定一个圆

3. 下列判断中，不正确的有(    )

A. 三边对应成比例的两个三角形相似
B. 两边对应成比例，且有一个角相等的两个三角形相似
C. 有一个锐角相等的两个直角三角形相似
D. 有一个角是的两个等腰三角形相似

4. 如果是等边三角形的一个内角，那么的值等于(    )

A.  B.  C.  D.

5. 在反比例函数图象的每一支曲线上，都随的增大而减小，则的取值范围是(    )

A.  B.  C.  D.

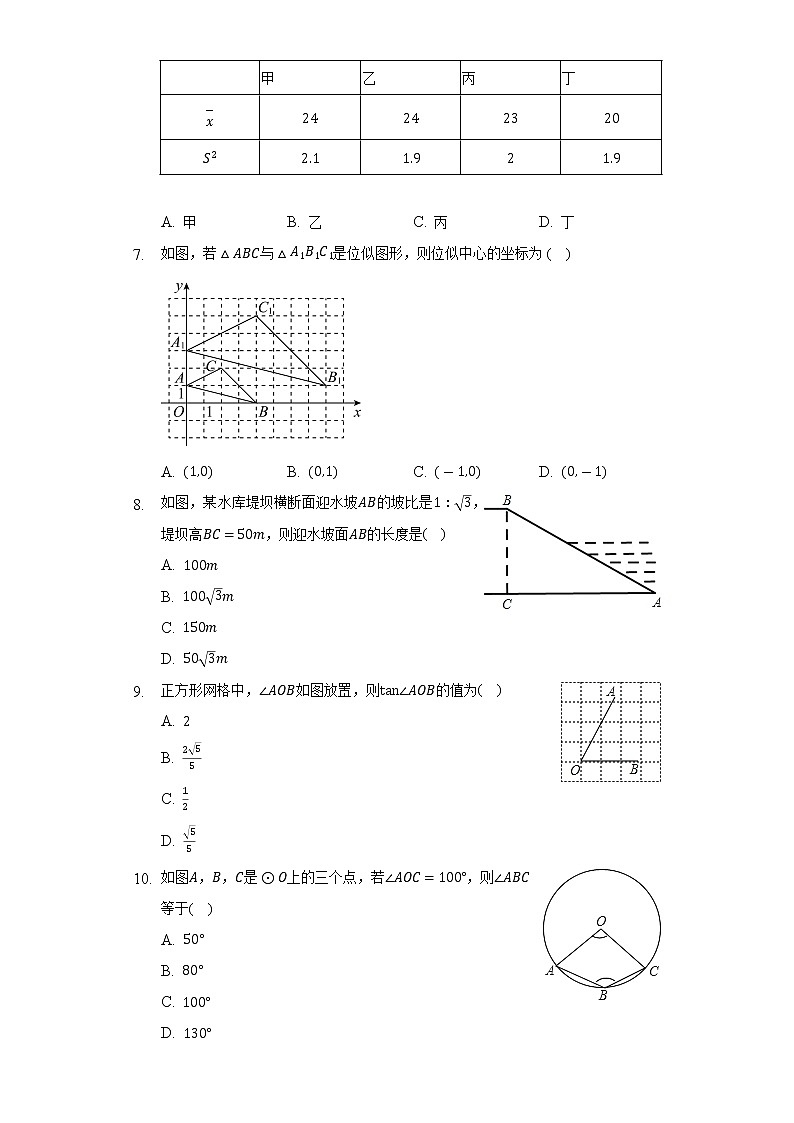
6. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各菜摘了棵，每棵产量的平均数单位：千克及方差单位：千克如表所示，今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是(    )

A. 甲 B. 乙 C. 丙 D. 丁

7. 如图，若与是位似图形，则位似中心的坐标为(    )

A.  B.  C.  D.

8. 如图，某水库堤坝横断面迎水坡的坡比是，堤坝高，则迎水坡面的长度是(    )

A.
B.
C.
D.

9. 正方形网格中，如图放置，则的值为(    )

A.
B.
C.
D.

10. 如图，，是上的三个点，若，则等于(    )

A.
B.
C.
D.

11. 一元二次方程配方，得，则和的值分别是(    )

A. ， B. ，
C. ， D. ，

12. 在同一平面直角坐标系中，函数和的图象大致是(    )

A.  B.
C.  D.

13. 如图，是的中位线，延长至使，连接，则的值为(    )
     

A.  B.  C.  D.

14. 如图，是的直径，弦交于点，且为的中点，，，则阴影部分的面积为(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共6小题，共18.0分）

15. 已知是的反比例函数，当时，，则这个函数关系式为______ ．
16. 已知一组数据，，，，，的平均数为，众数为，则这组数据的中位数是______．
17. 三角形两边的长是和，第三边的长是方程的根，则该三角形的周长为______．
18. 点、在反比例函数的图象上，若，则的范围是______．
19. 如图，在内画有边长为，，的三个正方形，则的值为______．
     
20. 如图，已知▱，，，以为直径的半圆与相切于点，则图中阴影部分的面积为______结果保留．

三、解答题（本大题共6小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）

21. 本小题分
    按要求解题：
    解方程：；
    计算：．
22. 本小题分
    如图，以为位似中心，在网格内作出四边形的位似图形，使新图形与原图形的相似比为：，并以为原点，写出新图形各点的坐标．

23. 本小题分
    平行四边形中，过作，垂足为，连为线段上一点，且求证：∽．

24. 本小题分
    钟南山院士谈到防护新型冠状病毒肺炎时说：“我们需要重视防护，尽量呆在家，勤洗手，多运动，多看书，少熬夜．”学校为鼓励学生抗疫期间在家阅读，组织八年级全体同学参加了疫期居家海量读书活动，随机抽查了部分同学读书本数的情况进行统计，如图所示：
    
    本次共抽查学生______人，并将条形统计图补充完整；
    读书本数的众数是______本，中位数是______本；
    在八年级名学生中，读书本及以上含本的学生估计有多少人？
25. 本小题分
    某商店代销一批季节性服装，每套代销成本元，第一个月每套销售定价为元时，可售出套；应市场变化调整第一个月的销售价，预计销售定价每增加元，销售量将减少套．
    若设第二个月的销售定价每套增加元，填写下表．

若商店预计要在这两个月的代销中获利元，则第二个月销售定价每套多少元？

26. 本小题分
    教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后接通电源，则自动开始加热，每分钟水温上升，待加热到，饮水机自动停止加热，水温开始下降．水温和通电时间成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为，接通电源后，水温和通电时间之间的关系如图所示，回答下列问题：
    
    分别求出当和时，和之间的函数关系式；
    求出图中的值；
    李老师这天早上：将饮水机电源打开，若他想在：上课前喝到不低于的开水，则他需要在什么时间段内接水？
    

答案和解析

1.【答案】 

【解析】解：，，，
，
方程有两个不相等的实数根．
故选A．
根据根的判别式的值的符号即可得．
本题考查了一元二次方程根的判别式的应用．
 

2.【答案】 

【解析】解：、在同圆或等圆中，长度相等的弧是等弧，所以选项错误；
B、圆既是轴对称图形，又是中心对称图形，所以选项正确；
C、弧不一定是半圆，而半圆是弧，所以选项错误；
D、不共线的三点确定一个圆，所以选项错误．
故选：．
根据等弧的定义对进行判断；根据轴对称图形和中心对称图形的定义对进行判断；根据弧的定义对进行判断；根据确定圆的条件对进行判断．
本题考查了圆的认识：圆可以看作是所有到定点的距离等于定长的点的集合；掌握与圆有关的概念弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等．
 

3.【答案】 

【解析】解：、三边对应成比例的两个三角形相似，故A选项不合题意；
B、两边对应成比例，且夹角相等的两个三角形相似，故B选项符合题意；
C、有一个锐角相等的两个直角三角形的三个角分别对应相等，所以两三角形相似，故C选项不合题意；
D、有一个角是的两个等腰三角形，则它们的底角都是，所以有一个角是的两个等腰三角形相似，故D选项不合题意．
故选：．
由相似三角形的判定依次判断可求解．
本题考查了相似三角形的判定，熟练运用相似三角形的判定是本题的关键．
 

4.【答案】 

【解析】解：是等边三角形的一个内角，
．
．
故选：．
根据等边三角形的性质及特殊角的三角函数值即可解答．
本题考查特殊角三角函数值的计算，特殊角三角函数值计算在中考中经常出现，要掌握特殊角度的三角函数值和等边三角形的性质．
 

5.【答案】 

【解析】解：在图象的每一支曲线上，都随的增大而减小，根据反比例函数的性质，
得，
．
故选：．
利用反比例函数的性质可得出，解不等式即可得出的取值范围．
本题考查了反比例函数的性质：
当时，图象分别位于第一、三象限；当时，图象分别位于第二、四象限．
当时，在同一个象限内，随的增大而减小；当时，在同一个象限，随的增大而增大．
 

6.【答案】 

【解析】解：因为甲组、乙组的平均数比丙组、丁组大，
而乙组的方差比丙组的小，
所以乙组的产量比较稳定，
所以产量既高又稳定的葡萄树进行种植，应选的品种是乙；
故选：．
先比较平均数得到甲组和乙组产量较好，然后比较方差得到乙组的状态稳定．
本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
 

7.【答案】 

【解析】

【解答】
解：如图所示：位似中心的坐标为．

故选：．
【分析】
此题主要考查了位似变换，正确掌握位似图形的性质是解题关键．
直接利用位似图形的性质得出位似中心即可．  

8.【答案】 

【解析】解：堤坝横断面迎水坡的坡比是，
，
，
，
，
故选：．
根据题意可得，把，代入即可算出的长，再利用勾股定理算出的长即可．
此题主要考查了解直角三角形的应用坡度问题，关键是掌握坡度是坡面的铅直高度和水平宽度的比．
 

9.【答案】 

【解析】解：由图可得，
故选：．
认真读图，在以为顶点的直角三角形里求的值．
本题考查锐角三角函数的概念：在直角三角形中，正切等于对边比邻边．
 

10.【答案】 

【解析】解：如图，在优弧上取点，连接，，
，
，
．
故选：．
首先在上取点，连接，，由圆周角定理即可求得的度数，然后由圆的内接四边形的性质，求得的度数．
本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
 

11.【答案】 

【解析】解：方程，配方得：，
整理得：，
由配方结果为，
，．
故选：．
方程配方后确定出所求即可．
此题考查了解一元二次方程配方法，熟练掌握完全平方公式是解本题的关键．
 

12.【答案】 

【解析】

【分析】
本题主要考查了反比例函数的图象和一次函数的图象，熟悉两函数中的符号对函数图象的影响是解题的关键．
分两种情况讨论，当时，分析出一次函数和反比例函数所过象限；再分析出时，一次函数和反比例函数所过象限，符合题意者即为正确答案．
【解答】
解：当时，过一、二、三象限；过一、三象限；
当时，过一、二、四象限；过二、四象限．
观察图形可知，只有选项符合题意．
故选：．  

13.【答案】 

【解析】

【分析】
本题考查了全等三角形、相似三角形的判定与性质，三角形中位线定理．关键是利用中位线判断相似三角形及相似比．先利用证明≌，得出，再由为中位线，判断∽，且相似比为：，利用相似三角形的面积比等于相似比，得到：：，则：：，进而得出：：．
【解答】

解：为的中位线，
．
在与中，
，
≌，
．
为的中位线，
∽，且相似比为：，
：：，
，
：：，
：：．
故选A．

14.【答案】 

【解析】

【分析】
本题主要考查了扇形的面积公式，圆周角定理，垂径定理，等边三角形的判定与性质，证明是等边三角形，得到，是本题的关键．首先证明是等边三角形，得到，，利用扇形的面积公式即可求解．
【解答】
解：如图所示，连接．

，
，
又，
是等边三角形，
为的中点，
，
是的直径，
，，
，，
，，
，
．
故选：．  

15.【答案】 

【解析】解：设反比例函数是，
当时，，代入可解得．
所以．
故答案为：．
根据反比例函数的定义设出表达式，再利用待定系数法解出系数则可．
本题考查了运用待定系数法求反比例函数的表达式，属于基本题型．
 

16.【答案】 

【解析】解：一组数据，，，，，的众数为，
，中至少有一个是，
一组数据，，，，，的平均数为，
，
，
，中一个是，另一个是，
这组数为，，，，，，
这组数据的中位数是，
故答案为：．
先判断出，中至少有一个是，再用平均数求出，即可得出结论．
本题考查了众数、平均数和中位数的知识，解答本题的关键是掌握各个知识点的概念．
 

17.【答案】 

【解析】解：解方程，
得，，
第三边，
第三边长为，
周长为．
先解一元二次方程，由于未说明两根哪个是腰哪个是底，故需分情况讨论，从而得到其周长．
此题是一元二次方程的解结合几何图形的性质的应用，注意分类讨论．
 

18.【答案】 

【解析】解：，
在图象的每一支上，随的增大而减小，
当点、在图象的同一支上，
，
，
解得：无解；
当点、在图象的两支上，
，
，，
解得：，
故答案为：．
根据反比例函数的性质分两种情况进行讨论，当点、在图象的同一支上时，当点、在图象的两支上时．
此题主要考查了反比例函数的性质，关键是掌握当时，在图象的每一支上，随的增大而减小．
 

19.【答案】 

【解析】解：如图，

这三个正方形的边都互相平行．
∽，
，
，
解得：．
故答案为．
由∽，可得 ，由此构建方程即可解决问题
本题考查相似三角形形的判定和性质，解题的关键是正确寻找相似三角形解决问题，学会构建方程解决问题．
 

20.【答案】 

【解析】解：连接，如图所示：
半圆与相切于点，
，
四边形为平行四边形，
，
，
，


．
故答案为：．
连接，求出，由即可得出结果．
此题考查了平行四边形的性质、切线的性质、平行四边形面积与三角形面积以及扇形面积的计算等知识；把不规则图形的面积转化为规则图形的面积是解决问题的关键．
 

21.【答案】解：，
，
，
或，
，；



． 

【解析】利用解一元二次方程因式分解法，进行计算即可解答；
把特殊角的三角函数值代入进行计算即可解答．
本题考查了解一元二次方程因式分解法，实数的运算，特殊角的三角函数值，准确熟练地进行计算是解题的关键．
 

22.【答案】解：如图所示，新图形为四边形，

新图形各点坐标分别为，，，． 

【解析】以为位似中心，作四边形的位似图形，使各边都扩大倍，再根据为原点，写出新图形各点的坐标即可．
此题考查了位似图形的作法，画位似图形的一般步骤为：确定位似中心；分别连接并延长位似中心和能代表原图的关键点；根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．
 

23.【答案】证明：四边形是平行四边形，
，，
，．
，，
，
∽． 

【解析】先根据平行线的性质得出，，再根据，可得出，由此可得出结论．
本题考查的是相似三角形的判定定理，熟知有两组角对应相等的两个三角形相似是解答此题的关键．
 

24.【答案】     

【解析】解：本次共抽查学生：人，
读书本的人数有：人，
补全的条形统计图如右图所示：

故答案为：；
由条形统计图可得，读书本数的众数是本，中位数是：本，
故答案为：；；
名，
答：读书本及以上含本的学生估计有人．
根据读书本的人数和所占的百分比，可以计算出本次共抽查的学生人数；计算出读书本的人数，从而可以将条形统计图补充完整；
根据众数和中位数的定义解答即可；
利用样本估计总体即可．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
 

25.【答案】解：若设第二个月的销售定价每套增加元，填写下表：

若设第二个月的销售定价每套增加元，根据题意得：
，
解得：舍去，，
当时，舍去，
当时，．
答：第二个月销售定价每套应为元． 

【解析】本题主要考查了一元二次方程的应用问题，在解题时要注意分析题意，找出等量关系．
本题先设第二个月的销售定价每套增加元，再分别求出销售量即可；
本题先设第二个月的销售定价每套增加元，根据题意找出等量关系列出方程，再把解得的代入即可．
 

26.【答案】解：当时，设，
将，的坐标分别代入得，
解得，．
当时，．
当时，设，
将的坐标代入，
得
当时，．
综上，当时，；当时，；

将代入，
解得，
即；

当时，．
要想喝到不低于的开水，需满足，
即李老师要在：到：之间接水． 

【解析】直接利用反比例函数解析式和一次函数解析式求法得出答案；
利用中所求解析式，当时，得出答案；
当时，代入反比例函数解析式，结合水温的变化得出答案．
此题主要考查了一次函数的应用及反比例函数的应用，正确求出函数解析式是解题关键．