2022-2023学年黑龙江省哈尔滨市巴彦县八年级（上）期中数学试卷（含解析）

2022-2023学年黑龙江省哈尔滨市巴彦县八年级（上）期中数学试卷

第I卷（选择题）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 点关于轴的对称点的坐标是(    )

A.  B.  C.  D.

2. 一个多边形的外角和比内角和大，则这个多边形的边数是(    )

A.  B.  C.  D.

3. 下列疫情防控宣传图片中，是轴对称图形的是(    )

A. 勤洗手，勤通风
B. 打喷嚏，捂口鼻
C. 有症状，早就医
D. 防控疫情，我们在一起

4. 如图，在和中，，，，，则的长为(    )

A.
B.
C.
D.

5. 如图，在中，，，为的中点，于点，若，则的长为(    )

A.  B.  C.  D.

6. 到三角形三个顶点距离相等的点是(    )

A. 三边高线的交点 B. 三边垂直平分线的交点
C. 三条中线的交点 D. 三条内角平分线的交点

7. 如图，和关于直线对称，若，，则的度数为(    )
    

A.
B.
C.
D.

8. 如图，中，，平分，交于点，，，则的长为(    )

A.
B.
C.
D.

9. 如图，中，，直线为的垂直平分线交于点，连接，则的周长为(    )

A.
B.
C.
D.

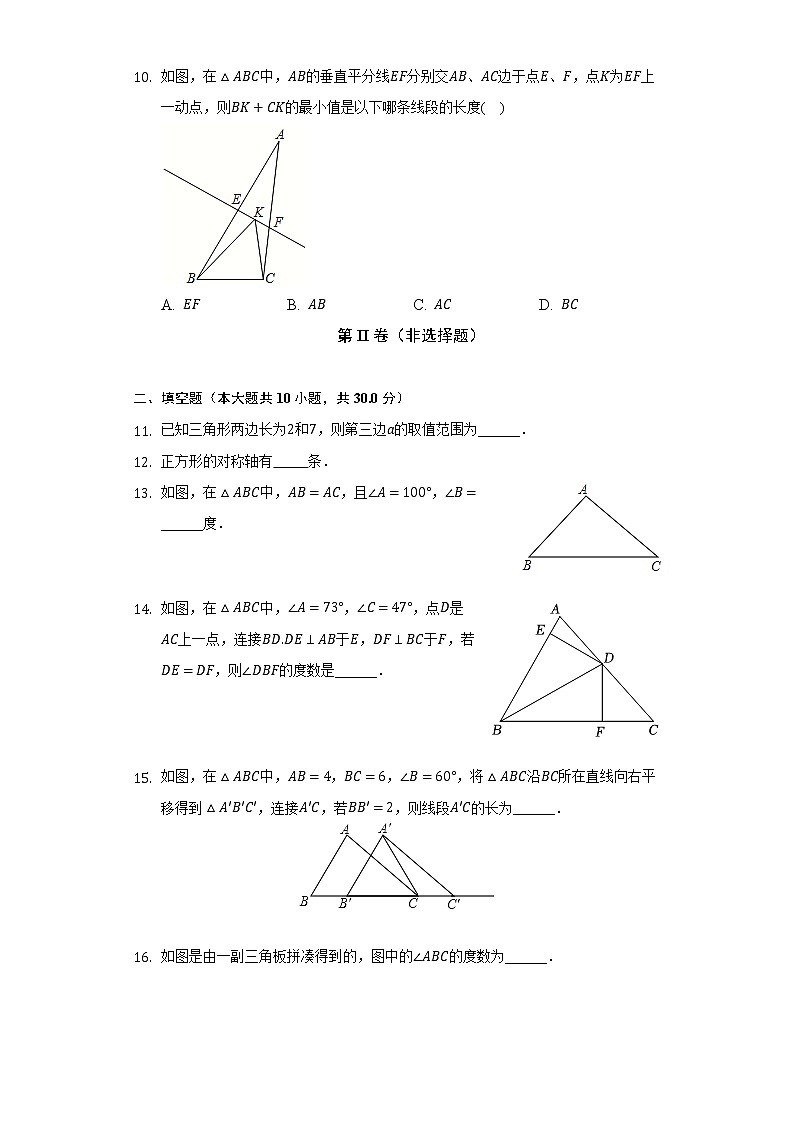
10. 如图，在中，的垂直平分线分别交、边于点、，点为上一动点，则的最小值是以下哪条线段的长度(    )
     

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共10小题，共30.0分）

11. 已知三角形两边长为和，则第三边的取值范围为______．
12. 正方形的对称轴有          条．
13. 如图，在中，，且，______度．

14. 如图，在中，，，点是上一点，连接于，于，若，则的度数是______．

15. 如图，在中，，，，将沿所在直线向右平移得到，连接，若，则线段的长为______．

16. 如图是由一副三角板拼凑得到的，图中的的度数为______．

17. 如图，是延长线上一点，交于点，，，若，，则的长是______．

18. 如图三角形纸片中，，，，沿过点的直线折叠这个三角形，使点落在边上的点处，折痕为，则的周长为______．

19. 等腰三角形的周长为，其中一边长为，则该等腰三角形的底边长为______．
20. 如图，在中，过点作的角平分线的垂线，垂足为，交于点，若，则线段的长为______．

三、解答题（本大题共7小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）

21. 本小题分
    如图，在中，，，的外角的平分线交的延长线于点，为延长线上的一点，连接．
    求的度数．
    若，求证：．

22. 本小题分
    如图，在平面直角坐标系中，，，．
    在图中作出，使与关于轴对称点、、的对称点分别为、、
    写出点、、的坐标．

23. 本小题分
    某市旧城改造项目计划在一块如图所示的三角形空地上种植某种草皮美化环境，经过测量得，的外角已知这种草皮每平方米元，则购买这种草皮一共需要多少钱？

24. 本小题分
    如图，，于，于，、交于点．
    求证：；
    如图，连接，请直接写出图中所有的全等三角形．
     
25. 本小题分
    如图，在中，，点是边上一点，且，平分交于点．
    若，求的度数；
    过点作，交于点，求证：．

26. 本小题分
    如图，在中，，点在边上，交的延长线于点．
    若，求证：；
    如图，连接，点为的中点，延长交于点，连接，若，求证：；
    如图，在的条件下，若，，点为的中点，求线段的长．
     
27. 本小题分
    如图，在平面直角坐标系中，点为坐标原点，的顶点、在轴上左右，点在轴正半轴上，，点为的中点，．
    求点的坐标；
    如图，点为上一点，点为轴上一点，，连接，，交轴于点，设线段的长为，线段的长为，请用含的式子表示；
    在的条件下，当点与点重合时，在的延长线上取点，作交轴于点，若，连接，过点作于点，求点的纵坐标．
    
    

答案和解析

1.【答案】 

【解析】解：点关于轴的对称点的坐标是．
故选D．
根据“关于轴对称的点，横坐标相同，纵坐标互为相反数”解答．
本题考查了关于轴、轴对称点的坐标，解决本题的关键是掌握好对称点的坐标规律：
关于轴对称的点，横坐标相同，纵坐标互为相反数；
关于轴对称的点，纵坐标相同，横坐标互为相反数；
关于原点对称的点，横坐标与纵坐标都互为相反数．
 

2.【答案】 

【解析】解：设这个多边形的边数是，
由题意得：，
，
故选：．
由多边形内角和定理：且为整数，多边形的外角和是，列出关于边数的方程即可求解．
本题考查多边形的有关知识，关键是掌握多边形内角和定理：且为整数，多边形的外角和是．
 

3.【答案】 

【解析】解：不是轴对称图形，故本选项不合题意；
B.不是轴对称图形，故本选项不合题意；
C.不是轴对称图形，故本选项不合题意；
D.是轴对称图形，故本选项符合题意．
故选：．
如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，根据轴对称图形的概念对各选项分析判断即可得解．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．轴对称图形的对称轴可以是一条，也可以是多条甚至无数条．
 

4.【答案】 

【解析】解：在与中，
，
≌，
，
，
故选：．
在与中，由证明两三角形全等得出，即可求解．
本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键．
 

5.【答案】 

【解析】解：，，
，
是的中点，
，
，
，
，
故选：．
由，推出，从而得到，
本题考查直角三角形的性质，等腰三角形的性质，关键是掌握：在直角三角形中，角所对的直角边等于斜边的一半；等腰三角形的两个底角相等．
 

6.【答案】 

【解析】解：到三角形三个顶点距离相等的点是三边垂直平分线的交点，
故选：．
根据线段垂直平分线的性质判断即可．
本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
 

7.【答案】 

【解析】

【分析】
本题考查的是轴对称的性质，熟知轴对称的两个图形全等是解答此题的关键．
先根据和关于直线对称得出≌，故可得出，再由三角形内角和定理即可得出结论．
【解答】
解：和关于直线对称，，，
≌，
，
．
故选：．  

8.【答案】 

【解析】解：如图，过点作于，
，平分，
，
，
解得：，
．
故选：．
过点作于，根据角平分线上的点到角的两边距离相等可得，然后利用的面积列式计算即可得解．
本题考查了三角形的面积和角平分线的性质，能熟记角平分线上的点到角两边的距离相等是解此题的关键．
 

9.【答案】 

【解析】解：直线是线段的垂直平分线，
，
的周长．
故选：．
根据中垂线的性质，可得，继而可确定的周长．
本题考查了线段垂直平分线的性质，掌握线段垂直平分线上任意一点，到线段两端点的距离相等是解决问题的关键．
 

10.【答案】 

【解析】解：连接，

是线段的垂直平分线，
，
，
的最小值即为的最小值，
当，，在同一直线上时，即与重合，最小，
即时，的值最小，即的值最小，
的最小值是线段的长度，
故选：．
连接，根据线段垂直平分线的性质得到，求得，得到的最小值的最小值，于是得到当时，的值最小，即的值最小，即可得到结论．
本题考查的是轴对称最短路线问题，线段垂直平分线的性质，三角形的三边关系，熟知线段垂直平分线的性质是解答此题的关键．
 

11.【答案】 

【解析】解：，，
第三边的取值范围为．
故答案为：．
利用“三角形的两边差小于第三边，三角形两边之和大于第三边”，可求出的取值范围．
本题考查了三角形三边关系，牢记“三角形的两边差小于第三边，三角形两边之和大于第三边”是解题的关键．
 

12.【答案】 

【解析】

【分析】
根据正方形的轴对称性作出图形以及对称轴，即可得解．
本题考查了轴对称的基本概念，熟记正方形的对称轴是解题的关键．
【解答】
解：如图，正方形对称轴为经过对边中点的直线，两条对角线所在的直线，共条．
故答案为：．
  

13.【答案】 

【解析】解：，
，
，
．
故填．
如图，依题意可知该三角形为等腰三角形，利用等腰三角形的性质得另外二角相等，结合三角形内角和易求的值．
本题考查了等腰三角形的性质：等边对等角和三角形内角和定理．借助三角形内角和求角的度数是一种很重要的方法，应熟练掌握．
 

14.【答案】 

【解析】解：，，
，
，，，
平分，
，
故答案为：．
先利用三角形内角和定理可得，再利用角平分线的性质定理的逆定理可得平分，然后利用角平分线的定义进行计算即可解答．
本题考查了角平分线的性质，熟练掌握角平分线的性质定理的逆定理是解题的关键．
 

15.【答案】 

【解析】解：由平移得：，，
，，
，
是等边三角形，
，
故答案为：．
利用平移可得，，再判定是等边三角形，进而可得答案．
此题主要考查了等边三角形的判定和性质，以及平移的性质，关键是掌握有一个角是的等腰三角形是等边三角形．
 

16.【答案】 

【解析】解：，，是的外角，
，
，
．
故答案为：．
由三角形的外角性质可求得，从而可求得的度数．
本题主要考查三角形的外角性质，解答的关键是明确三角形的外角等于与其不相邻的两个内角之和．
 

17.【答案】 

【解析】解：，
，，
在和中，
，
≌，
，
，
故答案为：．
由“”可证≌，可得，即可求解．
本题考查了全等三角形的判定和性质，证明三角形全等是解题的关键．
 

18.【答案】 

【解析】解：由折叠的性质得：，，
，
的周长，
故答案为：．
先根据折叠的性质可得，，再求出的长，然后求出的周长，即可得出答案．
本题考查了翻折变换的性质以及三角形周长；熟练掌握翻折变换的性质的解题的关键．
 

19.【答案】或 

【解析】解：当是等腰三角形的底边时，则其腰长是，能够组成三角形；
当是等腰三角形的腰时，则其底边是，能够组成三角形．
所以该等腰三角形的底边为或，
故答案为：或．
此题分为两种情况：是等腰三角形的底边或是等腰三角形的腰．然后进一步根据三角形的三边关系进行分析能否构成三角形．
此题考查了等腰三角形的两腰相等的性质，同时注意三角形的三边关系．
 

20.【答案】 

【解析】解：延长交于，
平分，
，
，
，
，
≌，
，
，
，
，
，
，
，
，
，
故答案为：．
延长交于，根据角平分线的定义得到，根据全等三角形的性质得到，根据平行线的性质得到，得到，推出．
本题考查了全等三角形的判定和性质，角平分线的定义，直角三角形的性质，平行线的性质，等腰三角形的判定和性质，正确地作出辅助线是解题的关键．
 

21.【答案】解：，，是的外角，
，
平分，
；
证明：，，
，
，
，
． 

【解析】由三角形的外角性质可求得，再由角平分线的定义即可求的度数；
结合可求得，利用同位角相等，两直线平行即可判定．
本题主要考查三角形的外角性质，平行线的判定，解答的关键是熟记三角形的外角等于与其不相邻的两个内角之和．
 

22.【答案】解：如图，为所作；

，，． 

【解析】利用网格特点和轴对称的性质画出点、、关于轴的对称点即可；
利用中所画图形求解．
本题考查了作图轴对称变换：作轴对称后的图形的依据是轴对称的性质，掌握其基本作法是解决问题的关键先确定图形的关键点；利用轴对称性质作出关键点的对称点；按原图形中的方式顺次连接对称点．
 

23.【答案】解：如图，过点作于点．

，
，
，
，
，
，
，
，
这种草皮每平方米元，
购买这种草皮一共需要元． 

【解析】如图，过点作于点证明，求出，再求出的面积，可得结论．
本题考查等腰三角形的性质，直角三角形度角的性质，三角形的面积等知识，解题的关键是转化添加常用辅助线，构造直角三角形解决问题．
 

24.【答案】证明：，，
，
在和中，
，
≌，
，
，
，
即；

解：图中全等三角形有≌，≌，≌，≌，
理由是：，，
，
在和中，
，
≌，
，，
根据可以证明≌和≌． 

【解析】根据垂直得出，根据全等三角形的判定定理可以证明≌，根据全等三角形的性质定理得出即可；
根据垂直得出，根据全等三角形的判定定理得出≌，根据全等三角形的性质得出，，再根据全等三角形的判定定理证明≌和≌即可．
本题考查了全等三角形的判定定理和性质定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有，，，，两直角三角形全等还有．
 

25.【答案】解：，
，
，
，
，
，
，
平分，
；
证明：设，则，
，
，
，
，
，
，
． 

【解析】首先利用三角形外角的性质求得，再利用三角形内角和求出的度数，从而得出答案；
设，则，利用平行线的性质和三角形内角和定理分别表示出和，从而解决问题．
本题主要考查了等腰三角形的性质，三角形内角和定理，平行线的性质等知识，利用参数分别表示出和是解题的关键．
 

26.【答案】证明：如图中，过点作于点，过点作于点，设交于点．

，，
，
，，
，
，
，
，，
，
，
，
，
，，
，
．

证明：如图中，

，
，
，
，，
，
，
，
，
；

解：过点作于点，交于点，连接，过点作于点．

，，
，
，，
，
，
，
，
，
，
，
，，，
，，
，
，
，
设，
，
，
，
，
，
，
． 

【解析】如图中，过点作于点，过点作于点，设交于点证明，可得结论；
证明垂直平分线段即可；
过点作于点，交于点，连接，过点作于点解直角三角形求出，，再利用勾股定理，可得结论．
本题属于三角形综合题，考查了等腰三角形的性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．
 

27.【答案】解：，为的中点，
垂直平分，
，
，
，
，
，
；
，，，
，
，
为等边三角形，
，，
又，
，
，
，
≌，
，
，
，
，
即；
过点作，交的延长线于点，连接，，，

，，
，
，
，
，
，，
又，
≌，
，
，，四边形的内角和为，
，
，
，
，
，，
，
为等边三角形，
，，
，，
≌，
，
，
，
，
，
，，
，
，，
点的纵坐标为． 

【解析】由线段垂直平分线的性质证出，由等腰三角形的性质得出，由直角三角形的性质求出的长，则可得出答案；
证出为等边三角形，由等边三角形的性质得出，，证明≌，由全等三角形的性质得出，则可得出答案；
过点作，交的延长线于点，连接，，，证明≌，由全等三角形的性质得出，证出为等边三角形，得出，，证明≌，由全等三角形的性质得出，证出，由等腰三角形的性质可得出答案．
本题是三角形综合题，考查了等腰三角形的性质，线段垂直平分线的性质，坐标与图形的性质，全等三角形的判定与性质，等边三角形的判定与性质，等腰直角三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键．