湖南省长沙麓山外国语实验中学2022-2023学年九年级上学期第一次限时训练数学试卷(解析版)

这是一份湖南省长沙麓山外国语实验中学2022-2023学年九年级上学期第一次限时训练数学试卷(解析版)，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
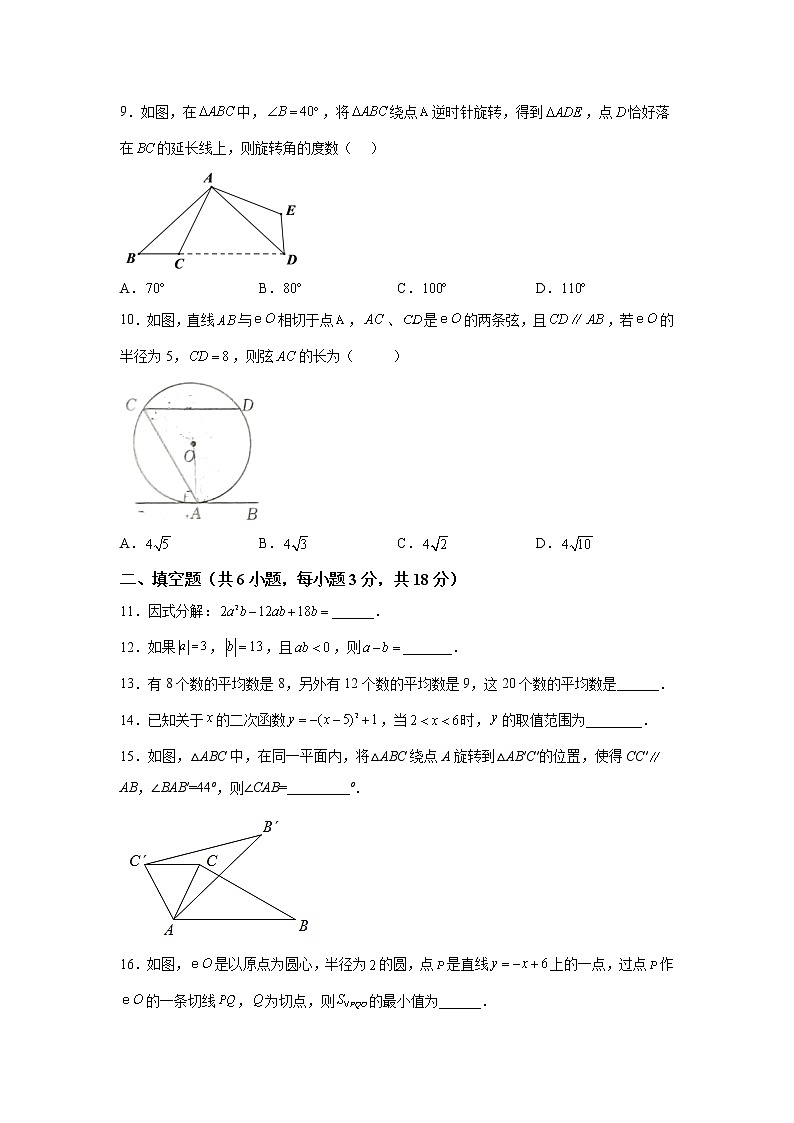
麓山外国语实验中学初三第一次限时训练数学试题卷一、选择题（共10小题，每小题3分，共30分）1．许多数学符号蕴含着对称美，在下列数学符号中，既是轴对称图形，又是中心对称图形的符号是（          ）A．∽ B．× C．⊥ D．∵2．下列运算中，正确的是（       ）A． B．C． D．3．大庆市2020年GDP超过了2800亿元，2800亿用科学记数法表示为（　　）A．2.8×103 B．28×1011 C．2.8×1012 D．2.8×10114．已知点在第二象限，且，则点M关于原点对称的点的坐标是（       ）A． B． C． D．5．下列说法正确的是（       ）A．平分弦的直径垂直于弦，并且平分弦所对的两条弧； B．圆的切线垂直于圆的半径；C．三角形的外心到三角形三边的距离相等； D．同弧或等弧所对的圆周角相等；6．已知一元二次方程x2﹣3x﹣3=0的两根为α与β，则的值为（　　）A．﹣1 B．1 C．﹣2 D．27．用一根绳子环绕一棵大树，若环绕大树3周，则绳子还多5尺；若环绕大树4周，则绳子又少了2尺，这根绳子有多长？环绕大树一周需要多少尺？设绳子有x尺，环绕大树一周需要y尺，所列方程组中正确的是（　　　）A． B．C． D．8．若不等式组的解集是x＞4，那么m的取值范围是（　　　）A． B． C． D．9．如图，在中，，将绕点逆时针旋转，得到，点恰好落在的延长线上，则旋转角的度数（   ）A． B． C． D．10．如图，直线与相切于点，、是的两条弦，且，若的半径为5，，则弦的长为（       ）A． B． C． D．二、填空题（共6小题，每小题3分，共18分）11．因式分解：______．12．如果，，且，则_______．13．有8个数的平均数是8，另外有12个数的平均数是9，这20个数的平均数是______．14．已知关于的二次函数，当时，的取值范围为________．15．如图，△ABC中，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′AB，∠BAB′=44º，则∠CAB=_________º．16．如图，是以原点为圆心，半径为的圆，点是直线上的一点，过点作的一条切线，为切点，则的最小值为______．三、解答题（共8小题，17-19题每小题6分，20-21题每小题8分，22-23题每小题9分，24-25题每小题10分，共72分）17．计算：．18．解不等式（组）．19．先化简：（﹣a+1）÷，并从0，﹣1，2中选一个合适的数作为a的值代入求值．20．已知直线与抛物线．(1)求证：直线l与该抛物线总有两个交点；(2)当时，求两交点坐标．21．如图，在中，，AD平分∠BAC，交BC于点D，DE⊥AB于E，点F在AC上，且．(1)求证：；(2)若，，求BE的长．22．如图，在中，对角线AC的垂直平分线分别与AD，AC，BC相交于点E，O，F．  (1)求证：四边形AFCE是菱形；(2)若∠BAC=90°，∠B=60°，AB=2，求DE的长．23．如图，内接于，，是的直径，点是延长线上的一点且．(1)求证：是的切线；(2)若，，求及的半径．24．定义：对于一次函数 ，我们称函数为函数的“组合函数”.(1)若m=3，n=1，试判断函数是否为函数的“组合函数”，并说明理由;(2)设函数与的图像相交于点P.①若，点P在函数的“组合函数”图像的上方，求p的取值范围；②若p≠1，函数的“组合函数”图像经过点P.是否存在大小确定的m值，对于不等于1的任意实数p，都有“组合函数”图像与x轴交点Q的位置不变?若存在，请求出m的值及此时点Q的坐标;若不存在，请说明理由.25．已知：为的直径，，为弦上一动点（不与、重合）．(1)如图1，若平分，连接交于点．①求证：；②若，求的长．(2)如图2，若绕点顺时针旋转得，连接．求证：为的切线． 
1．B【分析】根据轴对称图形与中心对称图形的概念求解．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．【详解】A．是中心对称图形，不是轴对称图形，故此选项不合题意；B．既是中心对称图形，也是轴对称图形，符合题意；C．是轴对称图形，不是中心对称图形，故此选项不合题意；D．是轴对称图形，不是中心对称图形，故此选项不合题意．故选：B．【点睛】本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．2．D【分析】根据幂的乘方，同底数幂相除，同底数幂相乘，积的乘方，逐项判断即可求解．【详解】解：A、，故本选项错误，不符合题意；B、，故本选项错误，不符合题意；C、，故本选项错误，不符合题意；D、，故本选项正确，符合题意；故选：D【点睛】本题主要考查了幂的乘方，同底数幂相除，同底数幂相乘，积的乘方，熟练掌握相关运算法则是解题的关键．3．D【分析】根据科学记数法的表示方法进行改写即可．【详解】2800亿，故选：D．【点睛】本题考查了科学记数法的表示方法，科学记数法的表示形式为，n为整数，正确确定a的值是解题的关键．4．D【分析】由题意，先求出，得到点M的坐标，然后求出关于原点对称的点的坐标即可．【详解】解：∵，∴，∵点在第二象限，∴，∴点，∴点M关于原点对称的点的坐标是；故选：D【点睛】此题主要考查了关于原点对称点的性质，解决本题的关键是掌握好对称点的坐标规律：关于原点对称的点，横坐标与纵坐标都互为相反数．5．D【分析】利用垂径定理、切线的性质、外心的性质及圆周角定理，分别判断后即可确定正确的选项．【详解】解：A、平分弦（不是直径）的直径必垂直于弦，且平分弦所对的两条弧，错误，是假命题；B、圆的切线垂直于过切点的的半径，故错误，是假命题；C、三角形的外心到三角形三个顶点的距离相等，故错误，是假命题；D、同弧或等弧所对的圆周角相等，正确，是真命题，故选：D．【点睛】本题考查了圆的有关知识，解题的关键是了解垂径定理、切线的性质、外心的性质及圆周角定理，难度不大．6．A【详解】试题分析：由一元二次方程根与系数关系得知:α＋β=-=3,αβ==-3,所求式子化为（α＋β）÷（αβ）=3÷（-3）=-1.故本题选A.考点：一元二次方程根与系数关系.7．D【分析】根据“若环绕大树3周，则绳子还多5尺；若环绕大树4周，则绳子又少了2尺”，列出二元一次方程组即可．【详解】解：由题意可得故选D．【点睛】此题考查的是二元一次方程组的应用，掌握实际问题中的等量关系是解题关键．8．D【分析】先求出第一个不等式的解集，再根据不等式组的解集是x＞4得出m的范围即可．【详解】解：，解不等式①，得x＞4，∵不等式组的解集是x＞4，∴m≤4，故选：D．【点睛】本题考查了解一元一次不等式组，能熟记求不等式组解集的规律（同小取小，同大取大，大小小大中间找，大大小小找不了）是解此题的关键．9．C【分析】由旋转的性质可知AB=AD，可算出∠ADB=40°，就可以算出旋转角．【详解】由旋转的性质可知：AB=AD，∠BAD是旋转角∵AB=AD∴∠ADB=∠B=40°∴∠BAD=180°-∠ADB-∠B=100°故选：C．【点睛】本题考查旋转的性质．找到旋转的对应边、对应角是解决问题的关键．10．A【分析】延长交于点E，连接．由题意可得，根据垂径定理求出，根据勾股定理可得，即可得，根据勾股定理可求的长．【详解】解：延长交于点E，连接．  ∵是切线，∴，又∵，∴即，∴，在中，，∴，在中，，故选A．【点睛】本题考查了切线的性质、垂径定理、勾股定理等知识点，添加辅助线构造直角三角形是解题的关键．11．【分析】原式提取公因式2b，再运用完全平方公式进行因式分解即可【详解】解：．故答案为：．【点睛】本题主要考查了综合运用提公因式法和公式法进行因式分解，熟练掌握完全平方公式是解答本题的关键．12．【分析】根据绝对值的性质可得，再由，可得a，b异号，即可求解．【详解】解∶∵，，∴，∵，∴a，b异号，当时，；当时，；综上所述，．故答案为：【点睛】本题考查了绝对值的性质，有理数的大小比较，有理数的减法运算，有理数的乘法，求得a，b的值是解题的关键．13．8.6【分析】根据平均数的公式求解即可，8个数的和加12个数的和除以20即可．【详解】解：由题意，得这些数之和为8×8＋12×9＝172，故这些数的平均数是=8.6．故答案为：8.6．【点睛】本题考查的是样本平均数的求法，正确地计算能力是解决问题的关键．14．【分析】根据函数解析式得出抛物线的对称轴，抛物线开口向下，当时，函数有最大值，距离对称轴越远，函数值越小，由此可解．【详解】解：∵二次函数解析式为，∴抛物线开口向下，对称轴为，∴在范围内，当时，函数有最大值，最大值为1，当时，函数有最小值，最小值为：，∴的取值范围为，故答案为：．【点睛】本题考查二次函数的图象及性质，能够根据二次函数解析式判断出抛物线的开口方向、对称轴，并熟练运用数形结合思想是解题的关键．15．68【分析】根据旋转的性质可得∠CAC′＝∠BAB′＝44°，AC＝AC′，然后利用等腰三角形的性质求出∠ACC′，再根据两直线平行，内错角相等解答．【详解】解：∵△ABC绕点A旋转得到△AB′C′，∴∠CAC′＝∠BAB′＝44°，AC＝AC′，∴∠AC′C＝∠ACC′＝，∵CC′AB，∴∠ACC′＝∠CAB＝68°，故答案为：68．【点睛】本题考查了旋转的性质，等腰三角形的性质，平行线的性质，熟记性质并准确识图是解题的关键．16．【分析】过点作于点，根据切线的性质得到，根据勾股定理用表示出，根据三角形的面积公式求出，得到答案．【详解】解：过点作于点，是的切线，，，是的半径，大小不变，当最小时，的面积最小，在中，，则当最小时，最小，对于直线，当时，，当时，，则，，由勾股定理得：，，则，解得：，当点与点重合时，最小，的最小值为，则的最小值为：，的最小值，故答案为：．【点睛】本题考查的是切线的性质、一次函数的图象和性质，掌握圆的切线垂直于经过切点的半径是解题的关键．17．【分析】根据二次根式的乘法，零指数次幂，立方根及实数的乘方分别计算即可．【详解】解：原式．【点睛】本题考查实数的混合运算，二次根式的乘法，零指数次幂，立方根等，解题关键是掌握相关的运算法则．18．【分析】分别求出两个不等式的解集，即可求解．【详解】解：，解不等式①得：， 解不等式②得：，所以原不等式组的解集为．【点睛】本题主要考查了解一元一次不等式组，熟练掌握解不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）是解题的关键．19．，1【分析】根据分式的加法和除法可以化简题目中的式子，然后在0，﹣1，2中选一个使得原分式有意义的值代入即可解答本题．【详解】解：，∵，，∴当时，原式．【点睛】本题考查了分式的化简求值，解答本题的关键是明确分式化简求值的方法．20．(1)见解析(2)（，），（，） 【分析】（1）令，证明Δ大于0．（2）将k＝−2代入直线解析式，联立两方程求解．（1）解：令，整理得，∵，∴直线l与该抛物线总有两个交点．（2）∵k＝−2，∴y＝−2x＋1，联立方程 ，解得， ，∴交点坐标为（，），（，）．【点睛】本题考查二次函数与一次函数的交点问题，解题关键是掌握函数与方程的关系．21．(1)见解析(2)6 【分析】（1）由角平分线的性质可得DC＝DE，根据HL可证得进而证得结论；（2）容易证得，则AC＝AE，分别用BE表示AC、AE，即可求出BE的长．（1）证明：∵AD平分∠BAC，DC⊥AC于C，DE⊥AB于E，∴DC＝DE，又DF＝BD，∴（HL），∴BE＝CF．（2）在和中，∵DE＝DF，AD＝AD，∴，∴AC＝AE，AB＝AE＋BE＝AC＋BE，AC＝AF＋CF，由（1）知CF＝BE，∴AB＝AF＋BE＋BE即，∴．【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，灵活运用角平分线的性质得出线段相等，进而证得两三角形全等是解题的关键．22．(1)见解析(2)2 【分析】（1）证△AOE≌△COF（ASA），得OE=OF，再由OA=OC，得四边形AFCE为平行四边形，然后由EF⊥AC，即可得出结论；（2）由含30°角的直角三角形的性质得BC=2AB=4，再证△ABF是等边三角形，得AF=AB=2，则AE=AF=2，即可得出答案．（1）证明：∵四边形ABCD为平行四边形，∴ADBC，∴∠EAO=∠FCO，∵EF垂直平分AC，∴OA=OC，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE=OF，又OA=OC，∴四边形AFCE为平行四边形，∵EF垂直平分AC，∴平行四边形AFCE是菱形．（2）解：∵∠BAC=90°，∠B=60°，AB=2，∴∠ACB=90°﹣∠B=30°，∴BC=2AB=4，∵四边形ABCD是平行四边形，∴AD=BC=4，由（1）可知，四边形AFCE是菱形，∴AE=AF=CF，∴∠FAC=∠ACB=30°，∴∠BAF=∠BAC﹣∠FAC=90°﹣30°=60°，∴∠B=∠BAF=60°，∴△ABF是等边三角形，∴AF=AB=2，∴AE=AF=2，∴DE=AD﹣AE=4﹣2=2．【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质、全等三角形的判定与性质、含30°角的直角三角形的性质、等边三角形的判定与性质、等腰三角形的性质等知识，熟练掌握菱形的判定与性质是解题的关键．23．(1)见解析(2)，的半径为3 【分析】（1）连接，先根据圆周角定理证明，从而得到，再根据圆周角定理可得，然后根据等腰三角形的性质可得，，即可求证；（2）过点C作于点E，根据锐角三角函数求出的长，即可根据勾股定理求出的长，然后在中，根据锐角三角函数求出的长，即可．（1）证明∶如图，连接，∵，∴，∴，∴，∵，∴，∴，即，∵是是的半径，∴是的切线；（2）解：如图，过点C作于点E，则，∵，，∴，，∵，∴，∴，∴，∵，∴，即的半径为3．【点睛】此题重点考查等腰三角形的性质、圆的切线的判定、圆周角定理、勾股定理、锐角三角函数等知识，正确地作出所需要的辅助线是解题的关键．24．(1)是函数的“组合函数”(2)①；②存在，见详解 【分析】（1）把m=3，n=1代入组合函数中，化简后进行判断即可；（2）①先求出点P的坐标和“组合函数”，把代入“组合函数”，再根据题意，列不等式求解即可；②将点P代入“组合函数”，整理得m+n=1，把n=1-m代入“组合函数”，消去n，把y=0代入解一元一次方程即可求解．（1）解：是函数的“组合函数”，理由：由函数的“组合函数”为：，把m=3，n=1代入上式，得，函数是函数的“组合函数”；（2）解：①解方程组得， 函数与的图像相交于点P，点P的坐标为，的“组合函数”为， ， ，点P在函数的“组合函数”图像的上方，，整理，得，，， p的取值范围为；②存在，理由如下：函数的“组合函数”图像经过点P．将点P的坐标代入“组合函数”，得， ，，，，将代入=，把y=0代入，得解得：，设，则， ，对于不等于1的任意实数p，存在“组合函数”图像与x轴交点Q的位置不变．【点睛】本题考查了一次函数的图像和性质，一次函数与不等式的关系，一次函数与一元一次方程，正确理解“组合函数”的定义是解本题的关键．25．(1)①见解析；②4(2)见解析 【分析】（1）①根据圆周角定理和平分，可得，即可求证；②取的中点G，连接，根据三角形中位线定理可得，，再根据，可得，即可求解；（3）在上截取，连接，证明，可得，从而得到，即可求证．（1）①证明∶∵为的直径，∴，∵，∴，∴，∴，∵平分，∴，∴，，∴，∴；②解：如图，取的中点G，连接，∵点O为的中点，∴，，∴，∵，∴，∴，∴；（2）证明：如图，在上截取，连接，∵，∴，∴，∵，∴，∴，根据旋转的性质得：，∴，∵，∴，∴，∴，∴，即，∵为半径，∴为的切线．【点睛】本题主要考查圆的综合知识，熟练掌握圆周角定理，全等三角形的判定和性质，三角形中位线定理等知识是解题的关键．