


- 2022郑州高二上学期期末考试语文PDF版含答案 试卷 0 次下载
- 2022郑州高二上学期期末考试英语含解析 试卷 1 次下载
- 2022郑州高二上学期期末考试地理含解析 试卷 1 次下载
- 2022郑州高二上学期期末考试历史含解析 试卷 0 次下载
- 2022郑州高二上学期期末考试生物含解析 试卷 0 次下载
2022郑州高二上学期期末考试数学(文)含解析
展开郑州市2021—2022学年上期期末考试
高二数学(文)试题卷
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设a,b,c非零实数,且,则( ).
A. B.
C. D.
【答案】C
【解析】
【分析】对于A、B、D:取特殊值否定结论;
对于C:利用作差法证明.
【详解】对于A:取符合已知条件,但是不成立.故A错误;
对于B:取符合已知条件,但是,所以不成立.故B错误;
对于C:因为,所以.故C正确;
对于D:取符合已知条件,但是,所以不成立.故D错误;
故选:C.
2. 在等差数列中,,则( ).
A. 9 B. 6 C. 3 D. 1
【答案】A
【解析】
【分析】直接由等差中项得到结果.
详解】由得.
故选:A.
3. 椭圆的长轴长是( ).
A. 3 B. 6 C. 9 D. 4
【答案】B
【解析】
【分析】根据椭圆方程有,即可确定长轴长.
【详解】由椭圆方程知:,故长轴长为6.
故选:B
4. 中,三边长之比为,则为( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不存在这样的三角形
【答案】C
【解析】
【分析】利用余弦定理可求得最大角的余弦值小于零,由此可知最大角为钝角.
【详解】设三边分别为,,,中的最大角为,
,为钝角,
为钝角三角形.
故选:C.
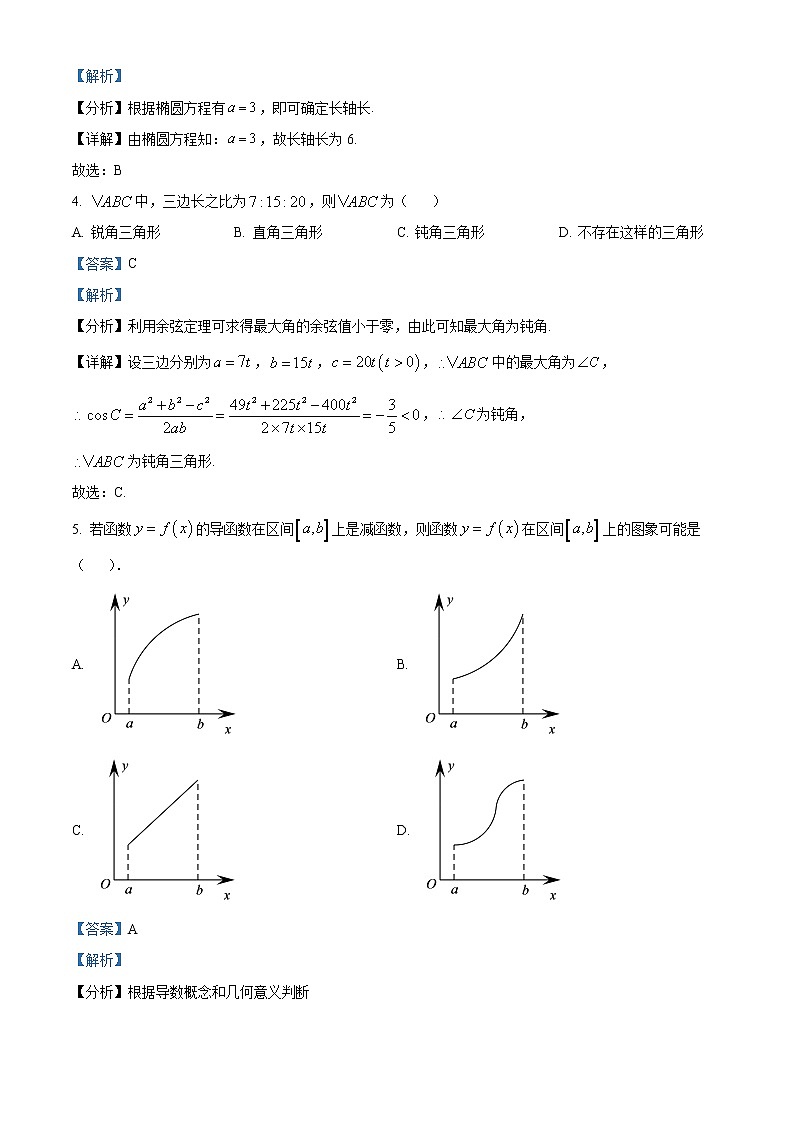
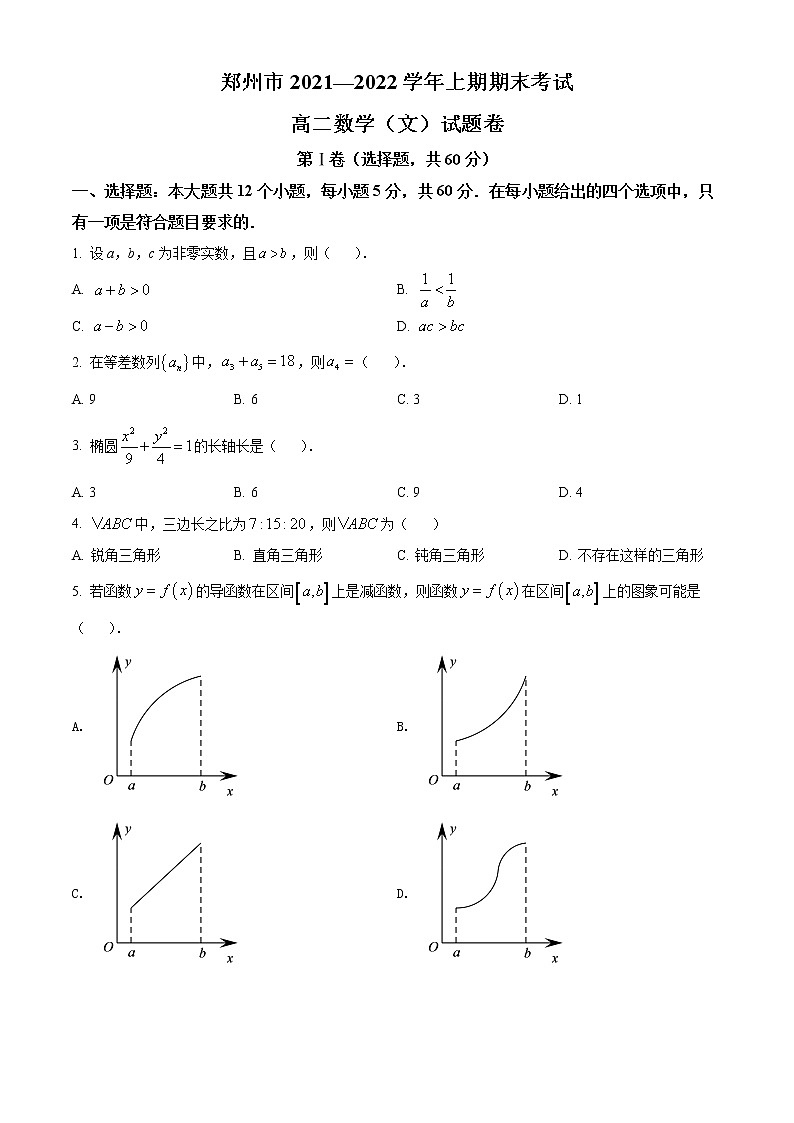
5. 若函数的导函数在区间上是减函数,则函数在区间上的图象可能是( ).
A. B.
C. D.
【答案】A
【解析】
【分析】根据导数概念和几何意义判断
【详解】由题意得,图象上某点处的切线斜率随增大而减小,满足要求的只有A
故选:A
6. 设变量x,y满足约束条件则目标函数的最小值为( ).
A. 3 B. 1 C. 0 D. ﹣1
【答案】C
【解析】
【分析】线性规划问题,作出可行域后,根据几何意义求解
【详解】作出可行域如图所示,,数形结合知过时取最小值
故选:C
7. 2021年11月,郑州二七罢工纪念塔入选全国职工爱国主义教育基地名单.某数学建模小组为测量塔的高度,获得了以下数据:甲同学在二七广场A地测得纪念塔顶D的仰角为45°,乙同学在二七广场B地测得纪念塔顶D的仰角为30°,塔底为C,(A,B,C在同一水平面上,平面ABC),测得,,则纪念塔的高CD为( ).
A. 40m B. 63m
C. m D. m
【答案】B
【解析】
【分析】设,先表示出,再利用余弦定理即可求解.
【详解】
如图所示,,设塔高为,因为平面ABC,所以,
所以,又,即,
解得.
故选:B.
8. 已知各项都为正数的等比数列,其公比为q,前n项和为,满足,且是与的等差中项,则下列选项正确的是( ).
A. B.
C D.
【答案】D
【解析】
【分析】根据题意求得,即可判断AB,再根据等比数列的通项公式即可判断C;再根据等比数列前项和公式即可判断D.
【详解】解:因为各项都为正数的等比数列,,
所以,
又因是与的等差中项,
所以,
即,解得或(舍去),故B错误;
所以,故A错误;
所以,故C错误;
所以,故D正确.
故选:D.
9. 设的内角的对边分别为的面积,则( )
A. B. C. D.
【答案】A
【解析】
【分析】利用三角形面积公式、二倍角正弦公式有,再由三角形内角的性质及余弦定理化简求即可.
【详解】由,
∴,在中,,
∴,解得.
故选:A.
10. 已知命题,;命题,,那么下列命题为假命题的是( ).
A. B.
C. D.
【答案】B
【解析】
【分析】由题设命题的描述判断、的真假,再判断其复合命题的真假即可.
【详解】对于命题,仅当时,故为假命题;
对于命题,由且开口向上,故为真命题;
所以为真命题,为假命题,
综上,为真,为假,为真,为真.
故选:B
11. 下列说法错误的是( ).
A. 命题“,”的否定是“,”
B. 若“”是“或”的充分不必要条件,则实数m的最大值为2021
C. “”是“函数在内有零点”的必要不充分条件
D. 已知,且,则的最小值为9
【答案】C
【解析】
【分析】对于A:用存在量词否定全称命题,直接判断;
对于B:根据充分不必要条件直接判断;
对于C:判断出“”是“函数在内有零点”的充分不必要条件,即可判断;
对于D:利用基本不等式求最值.
【详解】对于A:用存在量词否定全称命题,所以命题“,”的否定是“,”.故A正确;
对于B:若“”是“或”的充分不必要条件,所以,即实数m的最大值为2021.故B正确;
对于C:“函数在内有零点”,则,解得:或,所以“”是“函数在内有零点”的充分不必要条件.故C错误;
对于D:已知,且,所以(当且仅当,即时取等号)故D正确.
故选:C
12. 已知函数在上是增函数,则实数的取值范围是( )
A. B.
C. D.
【答案】A
【解析】
【分析】由题意可知,对任意的恒成立,可得出对任意的恒成立,利用基本不等式可求得实数的取值范围.
【详解】因为,则,
由题意可知,对任意的恒成立,所以,对任意的恒成立,
由基本不等式可得,当且仅当时,等号成立,
所以,.
故选:A.
第Ⅱ卷 非选择题(共90分)
二、填空题:本大题共4个小题,每小题5分,共20分.
13. 函数的图象在点处的切线方程为______.
【答案】
【解析】
【分析】求出、的值,利用点斜式可得出所求切线的方程.
【详解】因为,则,所以,,,
故所求切线方程为,即.
故答案为:.
14. 已知抛物线的焦点为,点在上,且,则______.
【答案】
【解析】
【分析】由抛物线的焦半径公式可求得的值.
【详解】抛物线的准线方程为,由抛物线的焦半径公式可得,解得.
故答案为:.
15. 已知数列,点在函数的图象上,则数列的前10项和是______.
【答案】
【解析】
【分析】将点代入可得,从而得,再由裂项相消法可求解.
【详解】由题意有,所以,
所以数列的前10项和为:
.
故答案为:
16. 若点P为双曲线上任意一点,则P满足性质:点P到右焦点的距离与它到直线的距离之比为离心率e,若C的右支上存在点Q,使得Q到左焦点的距离等于它到直线的距离的6倍,则双曲线的离心率的取值范围是______.
【答案】
【解析】
【分析】若Q到的距离为有,由题设有,结合双曲线离心率的性质,即可求离心率的范围.
【详解】由题意,,即,整理有,
所以或,
若Q到的距离为,则Q到左、右焦点的距离分别为、,又Q在C的右支上,
所以,则,又,
综上,双曲线的离心率的取值范围是.
故答案为:
【点睛】关键点点睛:若Q到的距离为,根据给定性质有Q到左、右焦点的距离分别为、,再由双曲线性质及已知条件列不等式组求离心率范围.
三、解答题:本大题共6小题,共70分,解答题应写出文字说明、证明过程或演算步骤.
17. △的内角A,B,C的对边分别为a,b,c.已知.
(1)求角B的大小;
(2)若△不为钝角三角形,且,,求△的面积.
【答案】(1)或;
(2).
【解析】
【分析】(1)根据正弦定理边角关系可得,再由三角形内角的性质求其大小即可.
(2)由(1)及题设有,应用余弦定理求得、,最后利用三角形面积公式求△的面积.
【小问1详解】
由正弦定理得:,又,
所以,又B为△的一个内角,则,
所以或;
【小问2详解】
由△不为钝角三角形,即,又,,
由余弦定理,,得(舍去负值),则.
∴.
18. 已知命题p:点在椭圆内;命题q:函数在R上单调递增.
(1)若p为真命题,求m的取值范围;
(2)若为假命题,求实数m的取值范围.
【答案】(1)
(2)
【解析】
分析】(1)根据题意列不等式组求解
(2)判断的真假性后分别求解
【小问1详解】
由题意得,解得且.
故m的取值范围是
【小问2详解】
∵为假命题,∴p和q都是真命题,
对于命题q,由题意得:恒成立,
∴,∴,
∴,解得.
故m的取值范围是
19. 设数列的前n项和为,且,数列.
(1)求和的通项公式;
(2)设数列的前n项和为,证明:.
【答案】(1),
(2)证明见解析
【解析】
【分析】(1)根据可得,从而可得;
(2)利用错位相减法可得,从而可得,又,即可证明不等式成立.
【小问1详解】
解:∵,∴当时,,
当时,,∴,
经检验,也符合,
∴,;
【小问2详解】
证明:因为,
∴,
∴
∴,
又∵,∴,
所以.
20. 已知函数.
(1)当时,求的单调区间与极值;
(2)若不等式在区间上恒成立,求k的取值范围.
【答案】(1)在上单调递增,在上单调递减,极大值为﹣1,无极小值
(2)
【解析】
【分析】(1)利用导数求出单调区间,即可求出极值;
(2)令,利用分离参数法得到,利用导数求出的最大值即可求解.
【小问1详解】
当时,,定义域为,.
当时,,单调递增;
当时,,单调递减.
∴当时,取得极大值﹣1.
所以在上单调递增,在上单调递减.
极大值为﹣1,无极小值.
【小问2详解】
由,得,
令,只需.
求导得,
所以当时,,单调递增,
当时,,单调递减,
∴当时,取得最大值,
∴k的取值范围为.
21. 球形物体天然萌,某食品厂沿袭老字号传统,独家制造并使用球形玻璃瓶用于售卖酸梅汤,其中瓶子的制造成本c(分)与瓶子的半径r(cm)的平方成正比,且当cm时,制造成本c为3.2π分,已知每出售1mL的酸梅汤,可获得0.2分,且制作的瓶子的最大半径为6cm.
(1)写出每瓶酸梅汤的利润y与r的关系式(提示:);
(2)瓶子半径多大时,每瓶酸梅汤的利润最大,最大为多少?(结果用含π的式子表示).
【答案】(1),
(2)当时,每瓶酸梅汤的利润最大,最大利润为28.8π
【解析】
【分析】(1)直接由条件写出关系式即可;
(2)直接求导确定单调性后,求出最大值即可.
【小问1详解】
设瓶子的制造成本c与瓶子的半径r的平方成正比的比例系数等于k,则瓶子的制造成本,由题意,当时,.
∴,即瓶子的制造成本.
∴每瓶酸梅汤的利润是,
∴每瓶酸梅汤的利润关于r的函数关系式为:,.
【小问2详解】
由(1)知,则,
令,则,
当时,;当时,.
∴函数在上单调递减,在上单调递增,
∴当时,每瓶酸梅汤的利润最大,最大利润为28.8π.
22. 从椭圆上一点P向x轴作垂线,垂足恰为左焦点,A是椭圆C与x轴正半轴的交点,直线AP的斜率为,若椭圆长轴长为8.
(1)求椭圆C的方程;
(2)点Q为椭圆上任意一点,求面积的最大值.
【答案】(1)
(2)18
【解析】
【分析】(1)易得,,进而有,再结合已知即可求解;
(2)由(1)易得直线AP的方程为,,设与直线AP平行的直线方程为,由题意,当该直线与椭圆相切时,记与AP距离比较远的直线与椭圆的切点为Q,此时的面积取得最大值,将代入椭圆方程,联立即可得与AP距离比较远的切线方程,从而即可求解.
【小问1详解】
解:由题意,将代入椭圆方程,得,
又∵,∴,化简得,解得,
又,,所以,
∴,
∴椭圆的方程为;
【小问2详解】
解:由(1)知,直线AP的方程为,即,
设与直线AP平行的直线方程为,
由题意,当该直线与椭圆相切时,记与AP距离比较远的直线与椭圆的切点为Q,此时的面积取得最大值,
将代入椭圆方程,化简可得,
由,即,解得,
所以与AP距离比较远的切线方程,
因为与之间的距离,又,
所以的面积的最大值为.
2024郑州高二上学期10月联考试题数学含解析: 这是一份2024郑州高二上学期10月联考试题数学含解析,共11页。
2022-2023学年四川省雅安市高二上学期期末考试数学(文)试题含解析: 这是一份2022-2023学年四川省雅安市高二上学期期末考试数学(文)试题含解析,共21页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省内江市高二上学期期末考试数学(文)试题含解析: 这是一份2022-2023学年四川省内江市高二上学期期末考试数学(文)试题含解析,共18页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












