福建省厦门市思明区逸夫中学2021-2022学年八年级上学期期中数学试卷（含答案）

这是一份福建省厦门市思明区逸夫中学2021-2022学年八年级上学期期中数学试卷（含答案），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（4分）计算的结果是
A．0B．1C．2D．
2．（4分）下列各式的计算结果为的是
A．B．C．D．
3．（4分）以下列各组线段长为边，不能组成三角形的是
A．，，B．，，
C．，，D．，，
4．（4分）运用完全平方公式计算，则公式中的是
A．B．C．D．
5．（4分）如图，点，分别在的边，上，点在线段上，则下列是的外角的是
A．B．C．D．
6．（4分）如图，在中，交边于点．设的重心为，若点在线段上，则下列结论正确的是
A．B．
C．的周长等于的周长D．的面积等于的面积
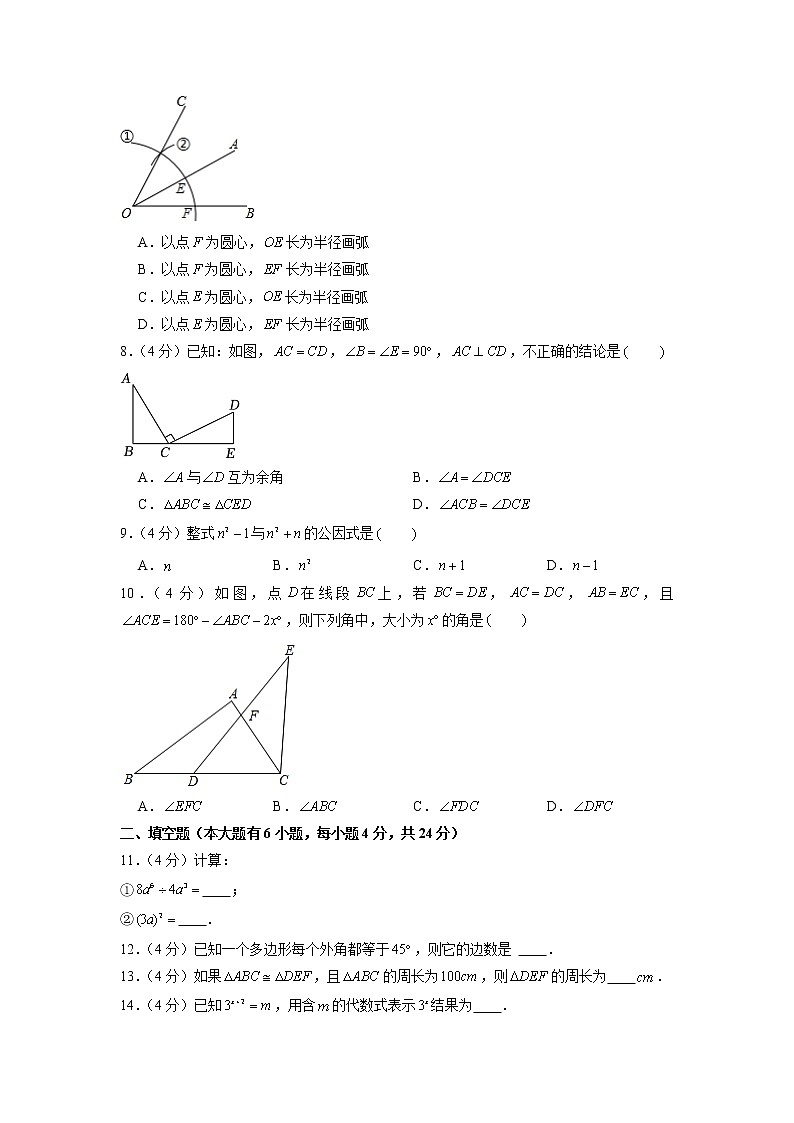
7．（4分）如图，用尺规作图作的第一步是以点为圆心，以任意长为半径画弧①，分别交、于点、，那么第二步的作图痕迹②的作法是
A．以点为圆心，长为半径画弧
B．以点为圆心，长为半径画弧
C．以点为圆心，长为半径画弧
D．以点为圆心，长为半径画弧
8．（4分）已知：如图，，，，不正确的结论是
A．与互为余角B．
C．D．
9．（4分）整式与的公因式是
A．B．C．D．
10．（4分）如图，点在线段上，若，，，且，则下列角中，大小为的角是
A．B．C．D．
二、填空题（本大题有6小题，每小题4分，共24分）
11．（4分）计算：
① ；
② ．
12．（4分）已知一个多边形每个外角都等于，则它的边数是 ．
13．（4分）如果，且的周长为，则的周长为 ．
14．（4分）已知，用含的代数式表示结果为 ．
15．（4分）如图，，是的两条高，，，，则的长为 ．
16．（4分）我国古代数学的许多创新与发展都曾居世界前列，其中“杨辉三角”（如图）就是一例，它的发现比欧洲早五百年左右．
杨辉三角两腰上的数都是1，其余每个数为它的上方（左右）两数之和，事实上，这个三角形给出了，2，3，4，5，的展开式（按的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应着展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着展开式中各项的系数，等等．
（1）当时，的展开式中第3项的系数是 ；
（2）人们发现，当是大于6的自然数时，这个规律依然成立，那么的展开式中各项的系数的和为 ．
三、解答题（本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤）
17．（8分）（1）计算：；
（2）计算：．
18．（8分）把下列多项式分解因式：
（1）；
（2）．
19．（7分）如图，点，，，在一条直线上，，，，求证：．
20．（8分）先化简，再求值：，其中，．
21．（8分）如图，在中，
（1）是的外角的平分线，且交的延长线于点（依题意补出图形）．
（2），，求的度数．
22．（10分）求证：三角形一边的两端点到这边的中线（或中线的延长线）的距离相等．（根据题意画图，写已知，求证，然后证明）
23．（11分）已知一些两位数相乘的算式：
，，，，，，，．
利用这些算式探究两位数乘法中可以简化运算的特殊情形：
（1）观察已知算式，选出具有共同特征的3个算式，并用文字描述它们的共同特征；
（2）分别计算你选出的算式．观察计算的结果，你能发现不经过乘法运算就可以快速、直接地写出积的规律吗？请用文字描述这个规律（计算结果与两位数因数之间的关系）；
（3）请用整式乘法的知识证明你发现的规律；
（4）在已知算式中，找出所有可以应用（或经过转化可以应用）上述规律的算式，并将它们写在横线上： ．
24．（12分）（阅读理解）
“若满足，求的值”
解：设，，则，，
所以
（解决问题）
（1）若满足，求的值．
（2）若满足，求的值．
（3）如图，正方形的边长为，，，长方形的面积是500，四边形和都是正方形，是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）．
25．（14分）如图，，，，，垂足为．
（1）求证：；
（2）求的度数；
（3）求证：．
2021-2022学年福建省厦门市思明区逸夫中学八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题有10小题，每小题4分，共40分）
1．（4分）计算的结果是
A．0B．1C．2D．
【解答】解：，
故选：．
2．（4分）下列各式的计算结果为的是
A．B．C．D．
【解答】解：、原式，故符合题意．
、原式，故不符合题意．
、原式，故不符合题意．
、原式，故不符合题意．
故选：．
3．（4分）以下列各组线段长为边，不能组成三角形的是
A．，，B．，，
C．，，D．，，
【解答】解：、，能组成三角形，故此选项不合题意；
、，不能组成三角形，故此选项符合题意；
、，能组成三角形，故此选项不合题意；
、，能组成三角形，故此选项不合题意；
故选：．
4．（4分）运用完全平方公式计算，则公式中的是
A．B．C．D．
【解答】解：由于，
所以完全平方公式中的是，
故选：．
5．（4分）如图，点，分别在的边，上，点在线段上，则下列是的外角的是
A．B．C．D．
【解答】解：的一个外角是，
故选：．
6．（4分）如图，在中，交边于点．设的重心为，若点在线段上，则下列结论正确的是
A．B．
C．的周长等于的周长D．的面积等于的面积
【解答】解：的重心为，
，为的中线，
，
．
故选：．
7．（4分）如图，用尺规作图作的第一步是以点为圆心，以任意长为半径画弧①，分别交、于点、，那么第二步的作图痕迹②的作法是
A．以点为圆心，长为半径画弧
B．以点为圆心，长为半径画弧
C．以点为圆心，长为半径画弧
D．以点为圆心，长为半径画弧
【解答】解：用尺规作图作的第一步是以点为圆心，以任意长为半径画弧①，分别交、于点、，
第二步的作图痕迹②的作法是以点为圆心，长为半径画弧．
故选：．
8．（4分）已知：如图，，，，不正确的结论是
A．与互为余角B．
C．D．
【解答】解：，
，
，
，
，
，
在和中，
，
，
，
，，
，
即和互余，
即只有选项错误，
故选：．
9．（4分）整式与的公因式是
A．B．C．D．
【解答】解：，，所以整式与的公因式是，
故选：．
10．（4分）如图，点在线段上，若，，，且，则下列角中，大小为的角是
A．B．C．D．
【解答】解：，，，
，
，，，
，
，
，
，
，
．
故选：．
二、填空题（本大题有6小题，每小题4分，共24分）
11．（4分）计算：
① ；
② ．
【解答】解：①，
故答案为：；
②，
故答案为：．
12．（4分）已知一个多边形每个外角都等于，则它的边数是 8 ．
【解答】解：多边形的外角和是，每个外角都等于，
，
正多边形的边数为8．
故答案为：8．
13．（4分）如果，且的周长为，则的周长为 100 ．
【解答】解：，
，，，
，
的周长，
故答案为：100．
14．（4分）已知，用含的代数式表示结果为 ．
【解答】解：，
．
．
故答案为：．
15．（4分）如图，，是的两条高，，，，则的长为 ．
【解答】解：，，
的面积，
，
，
，
故答案为：．
16．（4分）我国古代数学的许多创新与发展都曾居世界前列，其中“杨辉三角”（如图）就是一例，它的发现比欧洲早五百年左右．
杨辉三角两腰上的数都是1，其余每个数为它的上方（左右）两数之和，事实上，这个三角形给出了，2，3，4，5，的展开式（按的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应着展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着展开式中各项的系数，等等．
（1）当时，的展开式中第3项的系数是 6 ；
（2）人们发现，当是大于6的自然数时，这个规律依然成立，那么的展开式中各项的系数的和为 ．
【解答】解：（1）当时，的展开式中第3项的系数是6；
（2）人们发现，当是大于6的自然数时，这个规律依然成立，当时，各项系数分别为1，7，21，35，35，21，7，1，
那么的展开式中各项的系数的和为128，
故答案为：（1）6；（2）128
三、解答题（本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤）
17．（8分）（1）计算：；
（2）计算：．
【解答】解：（1）原式
；
（2）原式
．
18．（8分）把下列多项式分解因式：
（1）；
（2）．
【解答】解：（1）
；
（2）
．
19．（7分）如图，点，，，在一条直线上，，，，求证：．
【解答】证明：在和中，，
，
，
．
20．（8分）先化简，再求值：，其中，．
【解答】解：，
，
，
，
，
当，时，原式．
21．（8分）如图，在中，
（1）是的外角的平分线，且交的延长线于点（依题意补出图形）．
（2），，求的度数．
【解答】解：（1）如图所示：
（2），，
，
平分，
，
．
22．（10分）求证：三角形一边的两端点到这边的中线（或中线的延长线）的距离相等．（根据题意画图，写已知，求证，然后证明）
【解答】解：已知：如图所示，为的中线，且于，的延长线于．
求证：．
证明：为的中线．
，
，，
，
在和中，
，
，
．
23．（11分）已知一些两位数相乘的算式：
，，，，，，，．
利用这些算式探究两位数乘法中可以简化运算的特殊情形：
（1）观察已知算式，选出具有共同特征的3个算式，并用文字描述它们的共同特征；
（2）分别计算你选出的算式．观察计算的结果，你能发现不经过乘法运算就可以快速、直接地写出积的规律吗？请用文字描述这个规律（计算结果与两位数因数之间的关系）；
（3）请用整式乘法的知识证明你发现的规律；
（4）在已知算式中，找出所有可以应用（或经过转化可以应用）上述规律的算式，并将它们写在横线上： ， ．
【解答】（1）解：，，．
这3个算式共同特征是：一个两位数与11相乘；
（2）解：，，，
规律：两位数乘法中，如果有一个因数为11，得数的百位上的数是两个因数最高位上的积，十位上的数是第一个因数各个位数的和（满10进，个位上的数是两个因数个位上数的积；
如，
（3）证明：设一个两位数为，另一个数为11，
则它们的积为：；
（4）解：，
，
所以这些算式也可以利用此规律：，．
故答案为：，．
24．（12分）（阅读理解）
“若满足，求的值”
解：设，，则，，
所以
（解决问题）
（1）若满足，求的值．
（2）若满足，求的值．
（3）如图，正方形的边长为，，，长方形的面积是500，四边形和都是正方形，是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）．
【解答】解：（1）设，，
则，，
所以；
（2）设，，
则，，
；
（3）根据题意可得，
，，
，
设，，
则，，
．
所以图中阴影部分的面积为2100．
25．（14分）如图，，，，，垂足为．
（1）求证：；
（2）求的度数；
（3）求证：．
【解答】证明：（1），
，，
，
在和中，
，
；
（2），，
，
由（1）知，
，
，
，
，
；
（3）延长到，使得，
，
，
在和中，
，
，
，，
，
，，，
，，
，
，
在和中，
，
，
，
，
．