黑龙江省齐齐哈尔市克东县第二中学2021-2022学年八年级上学期期中数学试卷（含答案）

这是一份黑龙江省齐齐哈尔市克东县第二中学2021-2022学年八年级上学期期中数学试卷（含答案），共18页。试卷主要包含了下列运算正确的是，下列两个电子数字成轴对称的是，如图，，，那么等内容，欢迎下载使用。
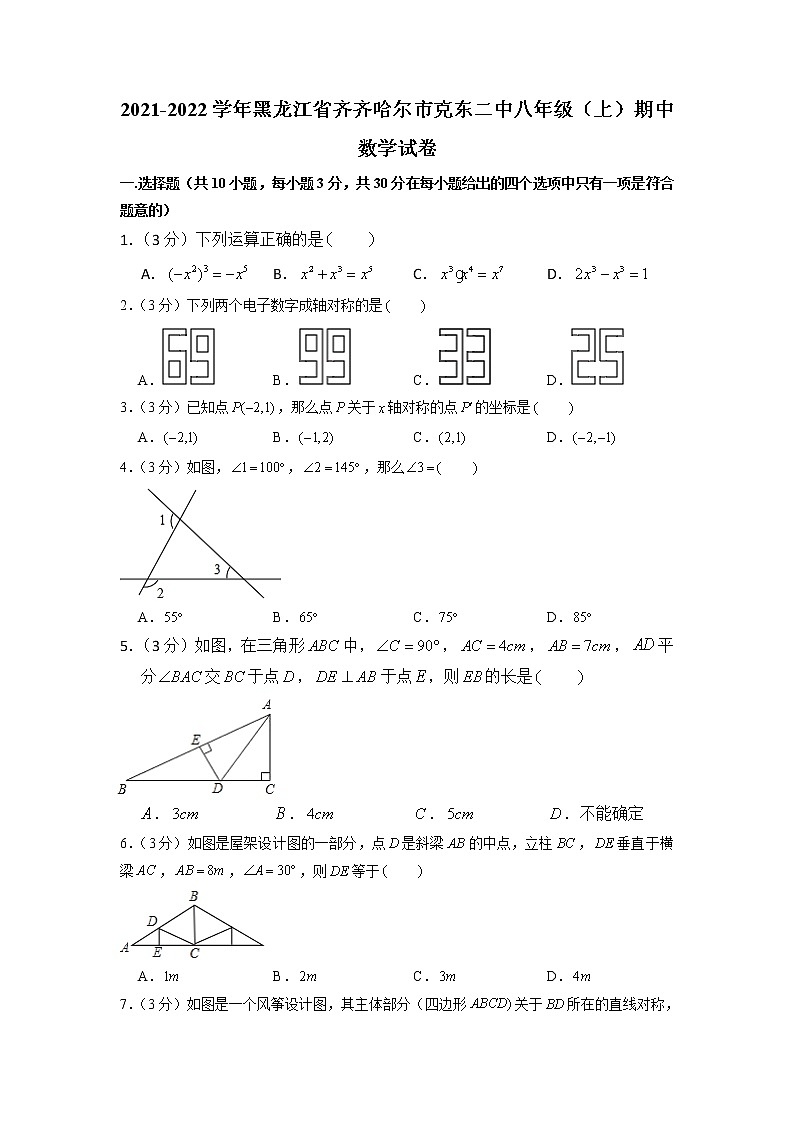
2021-2022学年黑龙江省齐齐哈尔市克东二中八年级（上）期中数学试卷一.选择题（共10小题，每小题3分，共30分在每小题给出的四个选项中只有一项是符合题意的）1．（3分）下列运算正确的是　　A． B． C． D．2．（3分）下列两个电子数字成轴对称的是　　A． B． C． D．3．（3分）已知点，那么点关于轴对称的点的坐标是　　A． B． C． D．4．（3分）如图，，，那么　　A． B． C． D．5．（3分）如图，在三角形中，，，，平分交于点，于点，则的长是　　． ． ． ．不能确定6．（3分）如图是屋架设计图的一部分，点是斜梁的中点，立柱，垂直于横梁，，，则等于　　A． B． C． D．7．（3分）如图是一个风筝设计图，其主体部分（四边形关于所在的直线对称，与相交于点，且，则下列判断不正确的是　　A． B． C． D．8．（3分）如图，把长方形纸片沿对角线折叠，设重叠部分为，那么，有下列说法：①是等腰三角形，；②折叠后和一定相等；③折叠后得到的图形是轴对称图形；④和一定是全等三角形．其中正确的有　　A．1个 B．2个 C．3个 D．4个9．（3分）已知，点在内部，与关于对称，与关于对称，则，，三点构成的三角形是　　A．直角三角形 B．等腰三角形 C．等边三角形 D．等腰直角三角形10．（3分）如图，在中，，的垂直平分线交于，连结，若的周长为23，则的长为　　A．6 B．7 C．8 D．9二.填空题（共10小题，每小题3分，共30分）11．（3分）已知中不含的三次项，则　　．12．（3分）若从一个多边形的一个顶点出发，最多可引8条对角线，则它是 　　边形．13．（3分）如图，已知，，的延长线交于，则图中全等的三角形共有　 　对．14．（3分）如图：作的角平分线的依据是　 　．（填全等三角形的一种判定方法）15．（3分）把两根钢条、的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），如图，若测得厘米，则槽宽为　　米．16．（3分）已知点关于轴的对称点的坐标是，则的值为　　．17．（3分）一个多边形，除了一个内角外，其余各角的和为，则这一内角为　　度．18．（3分）多项式的计算结果是，已知，由此可知多项式是 　　．19．（3分）若，，则　　．20．（3分）等腰三角形的周长为，一边长为，则底边长为　　．三.解答题（满分40分）21．（6分）已知，如图，在，，于，平分，，求的度数．22．（6分）如图，在平面直角坐标系中，，，．（1）如图中作出关于轴的对称图形△；（2）写出点，，的坐标（直接写答案）．　 　  　 　 　 　；（3）求的面积．23．（8分）如图，已知点、、在同一条直线上，和都是等边三角形．交于，交于，①求证：；②判断的形状并说明理由．24．（10分）如图1，为等边的边上一点，为延长线上一点，且，连接交于点．（1）求证：；（2）如图2，过作于，若，求的长．25．（10分）如图，已知中，、分别平分、，交于，连接，①直接写出与之间的关系式；②求证：为等腰三角形；③当的大小满足什么条件时，以、、为顶点的三角形为等腰三角形？
2021-2022学年黑龙江省齐齐哈尔市克东二中八年级（上）期中数学试卷参考答案与试题解析一.选择题（共10小题，每小题3分，共30分在每小题给出的四个选项中只有一项是符合题意的）1．（3分）下列运算正确的是　　A． B． C． D．【解答】解：、，此选项错误；、、不是同类项，不能合并，此选项错误；、，此选项正确；、，此选项错误；故选：．2．（3分）下列两个电子数字成轴对称的是　　A． B． C． D．【解答】解：选项，，的两个数字不是轴对称，选项中两个数字成轴对称，故选：．3．（3分）已知点，那么点关于轴对称的点的坐标是　　A． B． C． D．【解答】解：点与点关于轴对称，点，的坐标为．故选：．4．（3分）如图，，，那么　　A． B． C． D．【解答】解：，，，，，．故选：．5．（3分）如图，在三角形中，，，，平分交于点，于点，则的长是　　． ． ． ．不能确定【解答】解：平分交于点，，，，在和中，，，，，故选：．6．（3分）如图是屋架设计图的一部分，点是斜梁的中点，立柱，垂直于横梁，，，则等于　　A． B． C． D．【解答】解：如右图所示，立柱、垂直于横梁，，是中点，，，，是的中位线，，在中，，．故选：．7．（3分）如图是一个风筝设计图，其主体部分（四边形关于所在的直线对称，与相交于点，且，则下列判断不正确的是　　A． B． C． D．【解答】解：四边形关于所在的直线对称，，，，故、、判断正确；，和不全等，故判断不正确．故选：．8．（3分）如图，把长方形纸片沿对角线折叠，设重叠部分为，那么，有下列说法：①是等腰三角形，；②折叠后和一定相等；③折叠后得到的图形是轴对称图形；④和一定是全等三角形．其中正确的有　　A．1个 B．2个 C．3个 D．4个【解答】解：①是等腰三角形，，正确；②折叠后，和不一定相等（除非都是，故此说法错误；③折叠后得到的图形是轴对称图形，正确；④和一定是全等三角形，正确．故选：．9．（3分）已知，点在内部，与关于对称，与关于对称，则，，三点构成的三角形是　　A．直角三角形 B．等腰三角形 C．等边三角形 D．等腰直角三角形【解答】解：如图，连接，与关于对称，与关于对称，，，，，，，，，三点构成的三角形是等腰直角三角形．故选：．10．（3分）如图，在中，，的垂直平分线交于，连结，若的周长为23，则的长为　　A．6 B．7 C．8 D．9【解答】解：是线段的垂直平分线，，，的周长为23，，．故选：．二.填空题（共10小题，每小题3分，共30分）11．（3分）已知中不含的三次项，则　　．【解答】解：原式，原式不含的三次项，，．故答案为．12．（3分）若从一个多边形的一个顶点出发，最多可引8条对角线，则它是 　11　边形．【解答】解：从一个多边形的一个顶点出发，最多可引8条对角线，则它是11边形．故答案为：11．13．（3分）如图，已知，，的延长线交于，则图中全等的三角形共有　3　对．【解答】解：①，，；②，，；③，，图中全等的三角形共有3对．14．（3分）如图：作的角平分线的依据是　　．（填全等三角形的一种判定方法）【解答】解：在与中，，，是的平分线．故答案为：．15．（3分）把两根钢条、的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），如图，若测得厘米，则槽宽为　0.05　米．【解答】解：连接，，为和的中点，，，△，即，故，．故答案为0.05．16．（3分）已知点关于轴的对称点的坐标是，则的值为　2　．【解答】解：点关于轴的对称点的坐标是，，解得：，则的值为：2．故答案为：2．17．（3分）一个多边形，除了一个内角外，其余各角的和为，则这一内角为　130　度．【解答】解：设，解得，因而多边形的边数是18，则这一内角为度．故答案为：130．18．（3分）多项式的计算结果是，已知，由此可知多项式是 　　．【解答】解：多项式的计算结果是，已知，，故答案为：．19．（3分）若，，则　6　．【解答】解：，，原式，故答案为：6．20．（3分）等腰三角形的周长为，一边长为，则底边长为　6或8　．【解答】解：①是底边时，腰长，此时三角形的三边分别为、、，能组成三角形，②是腰长时，底边，此时三角形的三边分别为、、，能组成三角形，综上所述，底边长为6或．故答案为：6或8．三.解答题（满分40分）21．（6分）已知，如图，在，，于，平分，，求的度数．【解答】解：，，，，平分，．22．（6分）如图，在平面直角坐标系中，，，．（1）如图中作出关于轴的对称图形△；（2）写出点，，的坐标（直接写答案）．　　  　 　 　 　；（3）求的面积．【解答】解：（1）如图所示： （2），，． （3）的面积．23．（8分）如图，已知点、、在同一条直线上，和都是等边三角形．交于，交于，①求证：；②判断的形状并说明理由．【解答】①证明：和都是等边三角形，，，，在和中，，；②是等边三角形．理由如下：，．，．，在和中，，，；，，是等边三角形．24．（10分）如图1，为等边的边上一点，为延长线上一点，且，连接交于点．（1）求证：；（2）如图2，过作于，若，求的长．【解答】解：（1）如图1所示，点作交于点；是等边三角形，也是等边三角形，，，，，在和中，，，； （2）如图2所示，过作交于．，是等边三角形，，是等边三角形，，，，，，．在和中，，，，，，，，．25．（10分）如图，已知中，、分别平分、，交于，连接，①直接写出与之间的关系式；②求证：为等腰三角形；③当的大小满足什么条件时，以、、为顶点的三角形为等腰三角形？【解答】解：①．、分别平分、，交于，，，，．②作于，于，于，如图所示：、分别平分、，，，，平分，即，，，，，，，，，又，，，为等腰三角形；（3）①不可能舍去．②时，；根据题意，是等腰三角形，只能为底角，，，，，，．③时，设，则，，，，，综上所述，满足条件的的值为或．